ステータス
| 計算ステップ数: | 計算中... |
移動量/ステップ
| 最小 | 現在: | 最大 |
| 0 | 10 |
2次のモーメントの時間の指数
| 次数 | 現在 | 理論値 |
| 2次 | 計算中... | 1.0 |
プリミティブの種類
| gl.POINTS | |
| gl.LINE_STRIP | |
| gl.LINE_LOOP | |
| gl.LINES | |
| gl.TRIANGLE_STRIP | |
| gl.TRIANGLE_FAN | |
| gl.TRIANGLES |
計算アルゴリズム
ランダムウォークとはその名のとおり進行方向が時々刻々とランダムに変化するランダム粒子の運動のことである。
時刻 n に対する進行方向ベクトルを 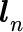 とした場合、
ランダム粒子の運動アルゴリズムを次に定義する。
とした場合、
ランダム粒子の運動アルゴリズムを次に定義する。
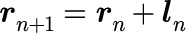
ただし、本稿では進行方向ベクトルは次の性質をみなすものとする。
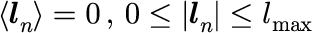
この系に対する統計的性質は解析的に計算することが可能で、例えば、1次のモーメント(平均)は
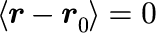
で、2次のモーメントは
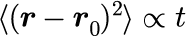
となる。時刻に対して指数が「1」(比例して増加)となる。 表にある「2次のモーメントの時間の指数」は本シミュレーションにおける計算結果から、 時刻に対する指数を次の手順でリアルタイムに計算している。
(1) 次の関係式にて、指数 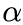 を定義
を定義
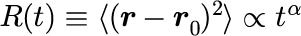
(2) 適当な時刻 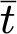 に対して次の関係があると仮定
に対して次の関係があると仮定
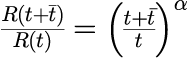
(3) 指数 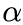 を次の式にて計算
を次の式にて計算
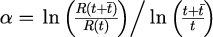
※この方法は非常に簡易的であるため、実際の研究などに利用する場合には注意が必要。