メトロポリス法を用いた、カノニカル集団の計算(3次元)

前回は、簡単のために１次元の場合の計算プログラムを実行したが、今回は３次元の場合を考える。
境界付近の粒子の取り扱い方については、境界に近い粒子（r_c<3、単位は粒子の直径）に、 隣のイメージセルからの影響をカウントするということで、周期的境界条件を課すという方法をとった。
今回は、力の切断距離を次のように導入する。

rx_c = L/2 , ry_c = L/2 , rz_c = L/2

これは、２粒子間の距離の３成分のうちどれかが L/2 を超えたときに、 その粒子との相互作用を無視して、その代わりにイメージセル内にある粒子からの相互作用をカウントする（下図）。

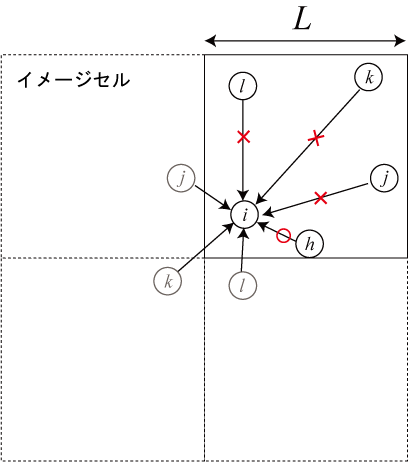
周期的境界条件を課したとき、イメージセルからの作用の模式図

これは、レナード・ジョーンズ・ポテンシャルのような、弱い引力(r^{-7})の場合には正当化される。

VisualC++ プログラムソース

2000モンテカルロステップの後（平衡状態）、1000ステップ分をサンプルする。
粒子数 N=100（一定）
粒子数密度 rho = 1.0, 0.1, 0.01, 0.001, 0.0001, 0.00001 (rho=N/V)
温度 T = 0.00001, 0.0001, 0.001, 0.01, 0.1, 1.0, 10, 100, 1000, 10000
セルの一辺 L = V^{1/3} = (rho/N)^{1/3}

/*
メトロポリス法を用いた、カノニカル集団の計算(3次元)
ポテンシャル：レナード・ジョーンズポテンシャル
*/
/*
メトロポリス(3次元)
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <sstream>
#include <string>
#include "mt19937ar.h"
#include <cstdio>
#include <iomanip>
#include <stdio.h>

using namespace std;

double PI = 3.1415926535897932384;
double e  = 2.7182818284590452354;

// 関数のプロトタイプ宣言
double phi_LJ( double r1_0, double r1_1, double r1_2, double r2_0, double r2_1, double r2_2, double L);

int main(){
  init_genrand((unsigned)time(NULL));

  int N = 100, monte_time=3000, t_0=2000;
  double R[100][3] = {0.0};
  double sigma = 1.0, L,T,rho,v,dl;
  double U_i=0.0, U_k= 0.0;
  
  v = 4.0 / 3.0 * PI * pow(sigma, 3);
  
  for(int rho_step=5 ; rho_step >= 0 ; rho_step--){
    rho = pow(10.0, -1.0 * double(rho_step));
    dl = pow(1.0/rho,1.0/3.0);
    L = pow(N/rho,1.0/3.0);
  
    for(int T_step=0 ; T_step <= 10 ; T_step++){
      T = pow(10.0, double(T_step - 5));
      for(int n=0; n<N; n++){
        for(int jj=0; jj<3;jj++) R[n][jj] = L * genrand_real1();
      }
      U_i = 0.0;
      //初期位置エネルギーの計算
      for(int i=0; i<N-1; i++ ){
        for(int j=i+1; j<N; j++ ){
          U_i += 4.0 * phi_LJ(R[i][0],R[i][1],R[i][2],R[j][0],R[j][1],R[j][2],L);
        }
      }
      //モンテカルロ計算開始
      for(int t=0; t<=monte_time;t++){
        cout << rho << " " << T <<  "-" <<t   << " potenshal=" << U_i <<endl;
        for(int n=0;n<N;n++){
  
          double dx = dl/2.0 * (1.0 - 2.0 * genrand_real1());
          double dy = dl/2.0 * (1.0 - 2.0 * genrand_real1());
          double dz = dl/2.0 * (1.0 - 2.0 * genrand_real1());
          R[n][0] += dx;
          R[n][1] += dy;
          R[n][2] += dz;
          if(R[n][0] > L) R[n][0] -= L;
          if(R[n][0] < 0) R[n][0] += L;
          if(R[n][1] > L) R[n][1] -= L;
          if(R[n][1] < 0) R[n][1] += L;
          if(R[n][2] > L) R[n][2] -= L;
          if(R[n][2] < 0) R[n][2] += L;
  
          U_k = 0.0;
          // ポテンシャルの計算
          for(int i=0; i<N-1; i++ ){
            for(int j=i+1; j<N; j++ ){
              U_k += 4.0 * phi_LJ(R[i][0],R[i][1],R[i][2],R[j][0],R[j][1],R[j][2],L);
            }
          }
          if(U_i < U_k){
            if(genrand_real1() > pow(e, -(U_k-U_i)/T)){
              R[n][0] -= dx;
              R[n][1] -= dy;
              R[n][2] -= dz;
              if(R[n][0] > L) R[n][0] -= L;
              if(R[n][0] < 0) R[n][0] += L;
              if(R[n][1] > L) R[n][1] -= L;
              if(R[n][1] < 0) R[n][1] += L;
              if(R[n][2] > L) R[n][2] -= L;
              if(R[n][2] < 0) R[n][2] += L;
            }
          }else{
            U_i = U_k;
          }
        }
        if(t>=t_0){
          //粒子座標表示
          ostringstream fname;
          fname <<  "data/position(" << rho_step << "-"  << T_step << "-" << t-t_0 << ").data";
          string fname2 = fname.str();
          ofstream fout_position;
          fout_position.open(fname2.c_str());
          for(int n=0; n<N; n++){
            fout_position << R[n][0] << " " <<  R[n][1] << " " <<  R[n][2] << endl;
          }
          fout_position.close();


        }
      }
    }
  }
}
double phi_LJ( double r1_0, double r1_1, double r1_2, double r2_0, double r2_1, double r2_2,double L){
	double rx , ry , rz ,Lh;
	Lh = L/2.0;
	rx = r1_0 - r2_0;
	ry = r1_1 - r2_1;
	rz = r1_2 - r2_2;
	if(rx > Lh) rx -= L;
	if(rx < -Lh) rx += L;
	if(ry > Lh) ry -= L;
	if(ry < -Lh) ry += L;
	if(rz > Lh) rz -= L;
	if(rz < -Lh) rz += L;
	double r2 = pow(rx,2) + pow(ry,2) + pow(rz,2) ;
	return  pow(1.0/r2,6) - pow(1.0/r2,3) ;
}

今後の予定

計算結果を用いて、 １．動径分布関数の計算
２．圧力の計算
３．静的構造因子の計算
を行う。