任意の周期関数のフーリエ級数を計算し、再び元の関数を再現する（C言語）

１．任意の周期関数をシンプソン法による求積を用いて（複素数）、フーリエ級数を計算する。

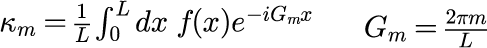
２．求めたフーリエ級数を用いて、元の関数を再現する。

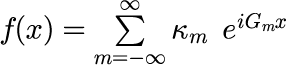
計算結果

先に解析的に求めたステップ関数のフーリエ級数と比較するために、同じステップ関数を用いる

κの値

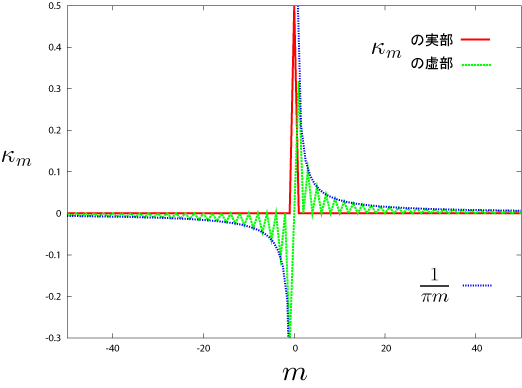
元の関数を再現

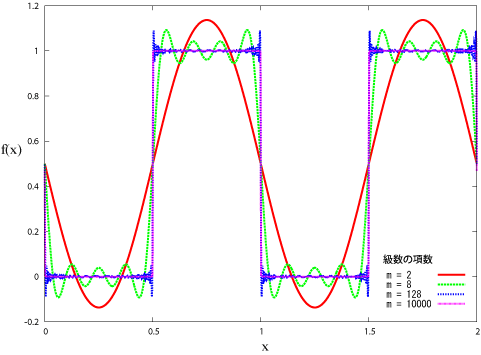
ソース（ステップ関数のフーリエ級数）

注意点

１．前回のシンプソン法による求積は実数であったものを、今回は複素数で取り扱い可能なものに変更。
２．大きな m_max （例えば m_max =10000） の場合には、シンプソン法の kizami をその10倍以上の値にしなければならない。
３．被積分関数に不連続点があれば、積分範囲のとり方を気をつける

/*
フーリエ級数をシンプソン法を用いて計算
計算例はステップ関数
F(x,m) 非積分関数
*/
#include <math.h>
#include <stdlib.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <iomanip>
#include <stdio.h>
#include <complex>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double>  I = complex<double>(0.0,1.0);

int kizami= 10000; //積分分割回数
double a = 1.0; // ステップの高さ
double L = 1.0; // 周期
double l = 0.5; // ステップの幅
double x_max =2.0; //描画範囲

complex<double> F(double);//被積分関数
complex<double> kappa_p[10000]; // m=[0, 10000]までをkappa の値を格納
complex<double> kappa_m[10000]; // m=[0,-10000]までのkappa の値を格納
complex<double> Simpson(double x0, double x1, int kizami, int m);

int main (void){
  for(int m_max = 2; m_max<=1024; m_max *= 2){
    kappa_p[0] = Simpson(0.0,L,kizami,0);
    for(int m=1 ; m<=m_max ; m++ ){
      int mm = -m;
      // 非積分関数が x = l で不連続なため、個別に計算する
      /*  0からlまでの積分 */
      kappa_p[m] = Simpson(0.0,l,kizami,m);
      kappa_m[m] = Simpson(0.0,l,kizami,mm);
      /*  lからLまでの積分 */
      kappa_p[m] += Simpson(l,L,kizami,m);
      kappa_m[m] += Simpson(l,L,kizami,mm);
      
    }
    /* ---------kappaの書き出し-------------------- */
    ostringstream fname2;
    fname2 << "kappa_2-" << m_max  << ".data";//出力ファイル名
    string fname2_s = fname2.str();
    ofstream fout2;
    fout2.open(fname2_s.c_str());
    for(int m=m_max ; m>0 ; m-- ){
      complex<double> z =  kappa_m[m];
      fout2 << -m << " " << z.real() << " " << z.imag() << endl;
    }
    for(int m=0 ; m<=m_max ; m++ ){
      complex<double> z =  kappa_p[m];
      fout2 << m << " " << z.real() << " " << z.imag() << endl;
    }
    fout2.close();
    /*---------------------------------------------*/

    ostringstream fname1;
    fname1 << "step_2-" << m_max  << ".data";//出力ファイル名
    string fname1_s = fname1.str();
    ofstream fout;
    fout.open(fname1_s.c_str());

    for(double x=0.0; x<=x_max ; x+=0.001){ 
      complex<double> sum =complex<double>(0.0,0.0);
      for(int m=1 ; m<=m_max ; m++ ){
        int mm = -m;
        sum += kappa_p[m] * exp( I*(2.0*PI*double(m)*x/L));
        sum += kappa_m[m] * exp(-I*(2.0*PI*double(m)*x/L));
      }
      complex<double> f = kappa_p[0] + sum;
      fout << x << " " << f.real() << " " << f.imag() << endl;
    }
    fout.close();
    cout << m_max << endl;
  }
return 0;
}

complex<double> F(double x ,int m) //非積分関数
{
  complex<double> ff;
  if(0<=x && x<l) ff = complex<double>(0.0,0.0);
  if(l<=x && x<L) ff = exp(-I*2.0*PI*double(m)*x/L) * a / L;
  return ff;
}

complex<double> Simpson(double x0 ,double x1 ,int N, int m) // 合成シンプソン法による求積
{
  complex<double> ss1 = complex<double>(0.0,0.0);
  for(int i=1; i<=N/2-1; i++){
    double x = x0 + (x1-x0)/double(N) * double(2*i);
    ss1 += F(x,m);
  }
  complex<double> ss2 = complex<double>(0.0,0.0);;
  for(int i=1; i<=N/2; i++){
    double x = x0 + (x1-x0)/double(N) * double(2*i-1);
    ss2 += F(x,m);
  }
  return  (x1-x0)/(3.0*double(N)) * ( F(x0,m)+F(x1,m) + 2.0 * ss1 + 4.0 * ss2 );
}