シンプソン法を利用して積分を数値計算する

シンプソン法とは積分を数値積分するための手法です。
被積分関数 f(x) を用いて次の手順で積分値を近似します。

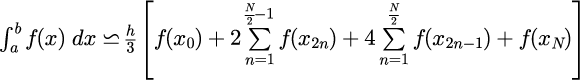
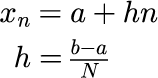
N は積分区間の分割数です。 N が大きくなるにつれ、積分区間を細かく足し合わせていきます。

計算誤差を確かめる

手計算できる積分とシンプソン法を用いた数値積分とを比較するために次の関数を用意します。

　　

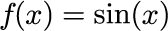
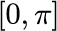
手計算では積分値は 2 です。 数値積分した結果から 2 を引いた値をプロットします。

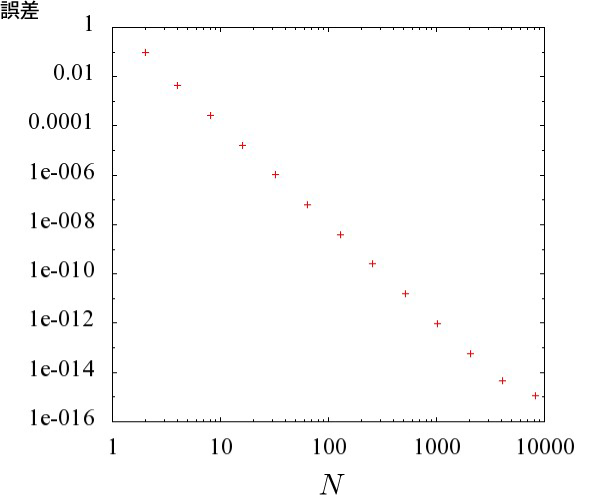
およそ、分割個数 N =1000 で誤差は 10^{-12} 程度となり、 誤差は h^{4}程度であることを確かめることができました。

C++プログラム

/////////////////////////////////////////////////
//シンプソン法
/////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
int N = 10000;
string folder = "1", ff="", fg="";  //保存フォルダ名
ostringstream fname;
double Simpson(double a ,double b ,int N);

double f(double x){
	return sin(x);
}

int main(){
 _mkdir(folder.c_str());
	ff = folder + "/f.data";     ofstream fout_f( ff.c_str());
  for(int i=2; i<=N; i=i*2){
    fout_f << i << " " << abs(Simpson(0,PI,i)-2.0) << endl;
  }
  return 0;
}
double Simpson(double a ,double b ,int N){
	double ss1 =0.0;
	for(int i=1; i<=N/2-1; i++){
		double x = a + (b-a)/double(N) * double(2*i);
		ss1 += f(x);
	}
	double ss2 =0.0;
	for(int i=1; i<=N/2; i++){
		double x = a + (b-a)/double(N) * double(2*i-1);
		ss2 += f(x);
	}
	return  (b-a)/(3.0*double(N)) * ( f(a) + f(b) + 2.0 * ss1 + 4.0 * ss2 );
}