【波動論4】
任意の周期関数をフーリエ変換+逆フーリエ変換する
【波動論1】フーリエ級数展開1:f=x、
【波動論2】フーリエ級数展開2:f=x^2では、解析的にフーリエ級数を計算し元の関数を再現できることを確かめました。
本節では、任意の周期関数を数値的にフーリエ級数展開します。
また、逆フーリエ変換を行うことで、元の関数になっていることを確かめます。
周期 L の場合のフーリエ級数展開
f(x) を任意の周期が L の関数とします。 f(x) は関数形が分かっている必要はなく、数値的なデータで問題ありません。 f(x) は次のように展開することができます。
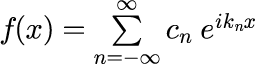
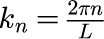
係数の c_n は、両辺に e^{-ik_mx}を掛けて区間で積分することで得られます(最後に m→n とする)。
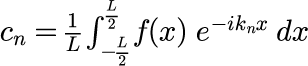
但し、積分を計算するときに、e^{ik_nx}と e^{ik_mx}が直交することを利用しています。
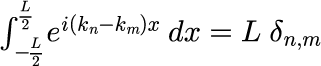
つまり、式(1)の展開する関数は区間で直交する関数であれば、どんなものでも利用できます。
計算結果
具体例として、次の関数のフーリエ級数の係数 c_n を数値的に計算します。
(※下の具体例は解析的に計算可能ですが。。。)
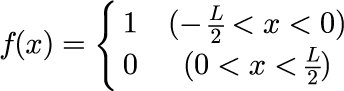
フーリエ級数の係数
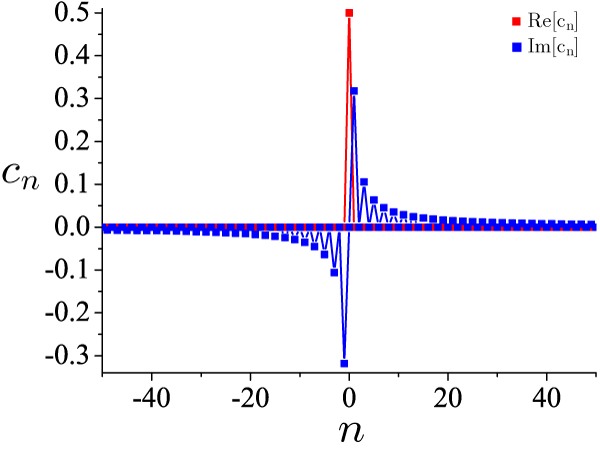
c_0 を除いて、c_n の虚数部のみ値を持ちます。 これは、f(x) が奇関数であることを意味し、sin 成分のみで記述できることと同義です。
フーリエ級数を用いて、元の関数を再現
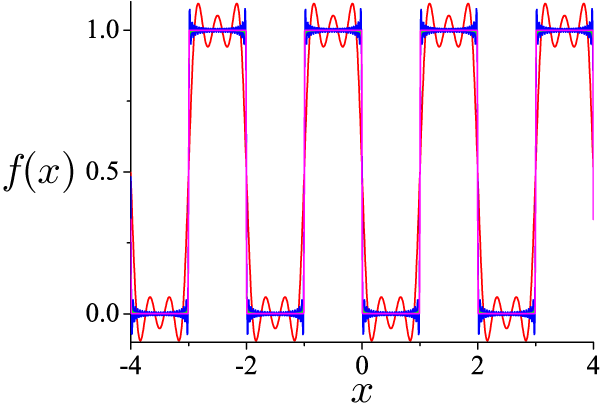
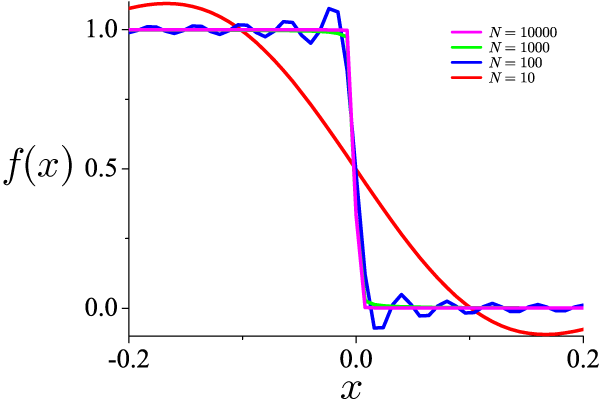
N は式(1)における和の数です。 N が大きくなるに従って、元の関数を忠実に再現していることが分かります。 x = 0 付近を拡大してみたものが下の図です。
任意の周期関数をフーリエ変換+逆フーリエ変換する C++プログラム
下のサンプルプログラムは、OpenMP を利用した並列計算も考慮しています。
「#pragma」利用して、OpenMP が利用できない環境でもコンパイルできるようになっています。
【参考】VisualC++ でOpenMPを利用した並列計算
式(2)の積分を計算するのに、シンプソン法を利用しています。
【参考】シンプソン法を利用して積分を数値計算する
/////////////////////////////////////////////////
//フーリエ級数展開_シンプソン法
//フーリエ級数展開+フーリエ級数の和
/////////////////////////////////////////////////
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
#include <omp.h>
#endif
#if defined(_MSC_VER)
#include <direct.h> // Windowsフォルダ作成用
#elif defined(__GNUC__)
#include <sys/stat.h> // UNIX系ディレクトリ作成用
#endif
using namespace std;
double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
const int N = 10000;
const int Nx = 1000; // x方向の分割の数
const int Ns = 20000; // 積分区間の分割の数(NとNsは同じにしてはいけない)
double L = 2.0;
string folder = "4", ff="", fg=""; //保存フォルダ名
ostringstream fname;
complex<double> FT_Simpson(double a ,double b ,int N, double k);
complex<double> K[N+1], F[Ns+1];
double f(double x){
if(x<0) return 1.0;
else return 0.0;
}
int main(){
#if defined(_MSC_VER)
_mkdir(folder.c_str()); // Windowsフォルダ作成
#elif defined(__GNUC__)
mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
#endif
#if defined(_OPENMP)
omp_set_num_threads(8);
cout << "OpenMPを利用します"<< endl;
cout << "最大スレッド数:"<< omp_get_max_threads() << endl;
#endif
clock_t time_start, time_end;
time_start = clock();
ff = folder + "/fk.data"; ofstream fout_fk( ff.c_str());
ff = folder + "/fx.data"; ofstream fout_fx( ff.c_str());
#pragma omp parallel
{
#pragma omp for //schedule(dynamic, 100)
for(int i=0; i<=N; i++){
double k = (2.0*PI/L) * double(i-N/2);
K[i] = FT_Simpson(-L/2.0, L/2.0, Ns, k)/L;
}
}
for(int i=0; i<=N; i++){
double k = (2.0*PI/L) * double(i-N/2);
fout_fk << i-N/2 << " " << K[i].real() << " " << K[i].imag() << endl;
}
#pragma omp parallel
{
#pragma omp for //schedule(dynamic, 100)
for(int i=0; i<=Nx; i++){
double x = L * double(i-Nx/2)/double(Nx) * 4.0;
F[i] = complex<double>(0.0,0.0);
for(int j=0; j<=N; j++){
double k = (2.0*PI/L) * double(j-N/2);
F[i] += K[j] * exp(I*k*x);
}
}
}
for(int i=0; i<=Nx; i++){
double x = L * double(i-Nx/2)/double(Nx) * 4.0;
fout_fx << x << " " << F[i].real() << " " << F[i].imag() << endl;
}
time_end = clock();
cout <<"計算時間は " << double(time_end - time_start)/double(CLOCKS_PER_SEC) << "でした" <<endl;
#if defined(_MSC_VER)
cin.get();//入力待ち
#endif
return 0;
}
complex<double> FT_Simpson(double a ,double b ,int N, double k){
complex<double> ss1 = complex<double>(0.0,0.0);
for(int i=1; i<=N/2-1; i++){
double x = a + (b-a)/double(N) * double(2*i);
ss1 += exp(-I*k*x) * f(x);
}
complex<double> ss2 = complex<double>(0.0,0.0);
for(int i=1; i<=N/2; i++){
double x = a + (b-a)/double(N) * double(2*i-1);
ss2 += exp(-I*k*x) * f(x);
}
return (b-a)/(3.0*double(N)) * ( exp(-I*k*a) * f(a) + exp(-I*k*b) * f(b) + 2.0 * ss1 + 4.0 * ss2 );
}
プログラムをちょっと解説
double f(double x){
if(x<0) return 1.0;
else return 0.0;
}
任意の関数を上記部分で指定します。
どんなに些細なものでも構いません。
コメント、ご指摘がございましたらこちらからお願い申し上げます。
































