確率論について

確率論について

　ある現象が次の状態になる時、その現象の前の状態から決定される。しかし、それは部分的にで、完全には依存してなく、確率的な予言しかできない。それらの偶然現象に対して数学的なモデルを与えて、解析する数学の一分野に、確率論というものがある。例えば、赤球が2つ、黒玉が３つ入った袋から、適当に球を１つずつ引き抜く時、1回目に黒玉を一つ引いたとする。次に球を引く時は、赤を引く確率も黒を引く確率も2分の1と同じである。しかし、もし1回目に赤球を引いていたとしたら、次に赤を引く確率は4分の1なのに対し、黒は4分の3で、黒を引く確率が高くなる。このように、確率的な予言しかできない物に対し、数学的なモデルを与えて解析する。

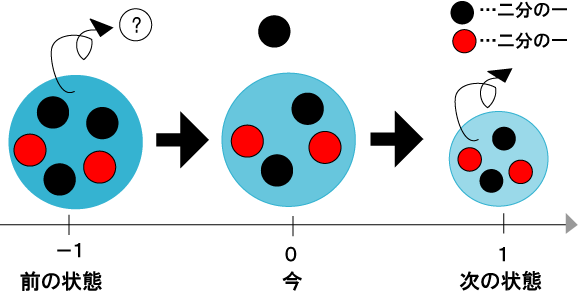
　自分は生物のアルゴリズム、特にアリの行動について考えていく。例えば、アリを空間内に置いた時、自由に方向を決め、歩き回る。その方向の決め方を乱数を使い、空間全体を歩くのにどれくらいかかったかなどを調べる。

途中経過

　まずは初歩として、０の位置に100個あった時、1個ずつ乱数で０だったら－１、1だったら＋１と位置をずらす。これを繰り返し行った時、最終的には100個がどのように分布するのかを調べている。

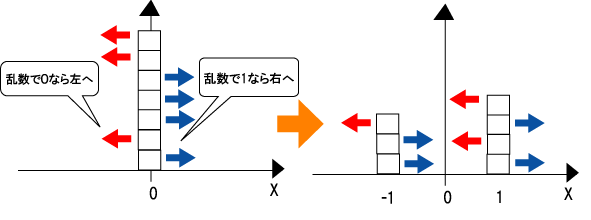
　上記のようなC言語でプログラムを作成し、5000回繰り返し、500回ごとにデータを書き出すというプログラムにした。 3回分のデータを集計し、見比べてみた。

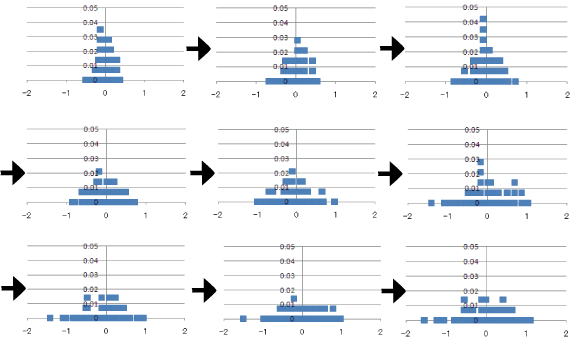
この結果から、回数が増えていくにつれ、全体的に広がっていくのがわかる。 ほかの結果も、似たような結果が出ていることから、回数を増やしていくにつれ、最初は0に100個あったのが、全体的に広がっていき、均衡になることが考えられる。