HTML5による物理シミュレーション環境の構築
水素原子の波動関数ビューア

文責：遠藤理平（2012年4月 6日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

HTML5の新要素 canvas 要素に WebGL（Three.js）＋Javascript を利用して構築する物理シミュレータの第３弾として、「水素原子の波動関数ビューア」を公開します。 水素原子は、陽子１つと電子１つで構成される最も単純な構造の原子です。電子はクーロン相互作用の引力により、電子よりも2000倍重たい陽子の周りに雲のように分布します（電子雲）。電子状態は、主量子数 $\,n$ , 方位量子数 $\,l$ , 磁気量子数 $\,m$ ３つのパラメータで指定され、それぞれ特徴的な形状を成します。本稿では HTML5 を水素原子の電子状態を表す波動関数の３次元空間分布を可視化するためのビューアとして利用します。

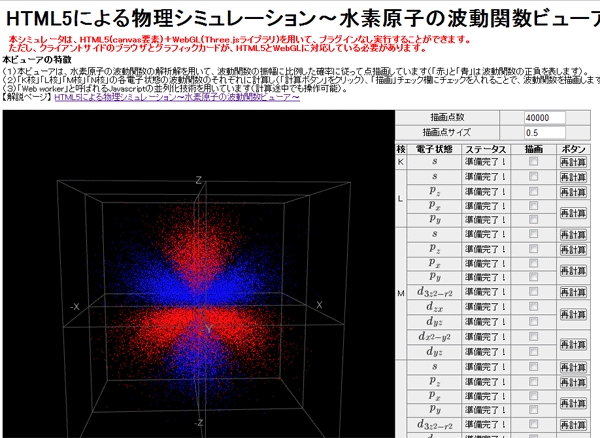
以下の図はデモ画面です → 実行ページこちら

計算アルゴリズム

水素原子の電子状態は、電子のように非常に小さな粒子が従うシュレーディンガー方程式を解くことで理解することができます。電子状態を表す波動関数に対するシュレーディンガー方程式は、その他の原子の場合と異なり、解析的に解くことができます。解析解は、主量子数 $\,n$ , 方位量子数 $\,l$ , 磁気量子数 $\,m$ の３つのパラメータを用いて、

(1)

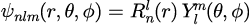
と表されます。 $\,R$ と $\,Y$ は、元のシュレーディンガー方程式を変数分離した際に得られる動径方向と方位角方向の解で

(2)

と

(3)

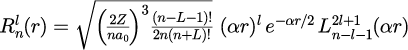
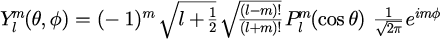
となります。式(2),(3)にある $\,L$ はラゲール多項式, $\,P$ はルジャンドル陪関数を表し、

(4)

(5)

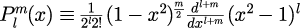
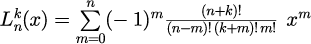
で定義されます。ラゲール多項式は階乗を計算できれば簡単に計算することができますが、ルジャンドル陪関数は、複数回の微分を演算する必要があるため、簡単に計算することできません。しかしながら、漸化式を用いることで比較的簡単に計算することができます。
※ルジャンドル陪関数については「ルジャンドル陪関数の漸化式と規格化」を参考にして下さい。

式中の $\alpha r$ は長さの表す無次元量です。本ビューアは、 $\alpha$ を単位として、１辺の長さ $\,L=80$ の立方体を描画しています。ただし、 $\alpha$ は

(6)

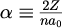
で定義され、 $\,a_0$ はボーア半径と呼ばれ

(7)

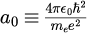
と定義されます。

スクリーンショット

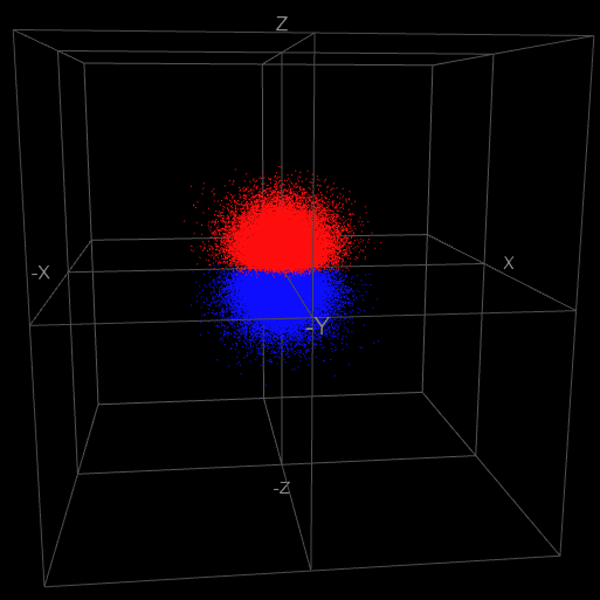
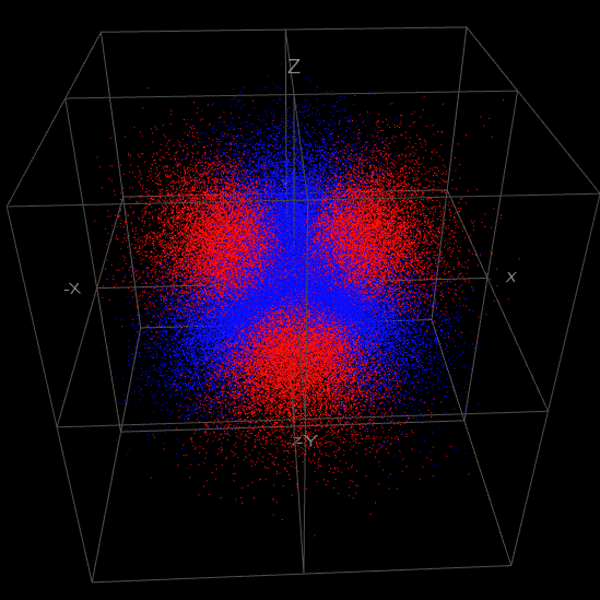
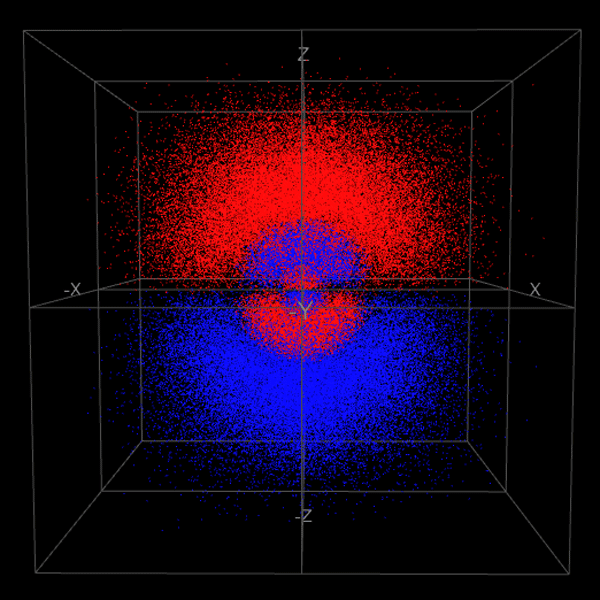
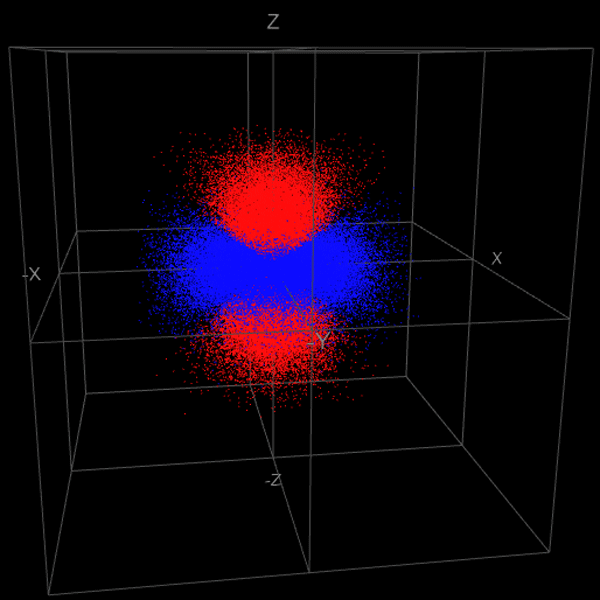
プログラムソース

Javascript

本ビューアは「WebWorker」と呼ばれる Javascript にて並列化計算を行うための技術を利用しています。 WebWorker も WeBGL と同様に、HTML5 における Javascript の標準化技術です。

本体

  var L = 80;       //系のサイズ
  var n_max = 4;    //主量子数の最大値
  var p_max = 40000;//点の数
  var p_size = 0.5; //点のサイズ
  var times, timesL;

  var scatterPlots = new Array(n_max+1);
  var workers = new Array(n_max+1);
  var $id = function(id) { return document.getElementById(id); }

  function init(){
    //各状態のオブジェクトとワーカーの多重配列を宣言
    for (var n = 1; n <= n_max; n++) {
      scatterPlots[n] = new Array(n);
      workers[n] = new Array(n);
      for (var l = 0; l < n; l++) {  
        scatterPlots[n][l] = new Array(l+1);
        workers[n][l] = new Array(l+1);
        for(m=0; m<=l; m++)  scatterPlots[n][l][m] = new Array(3);
      }
    }
    //ワーカーの設定
    for (var n = 1; n <= n_max; n++){
      for (var l = 0; l < n; l++){
        for (var m = 0; m <= l; m++){
          workers[n][l][m] = new Worker("worker_wave.js");
          for(var i=0; i<=2; i++) scatterPlots[n][l][m][i] = new THREE.Object3D();
          workers[n][l][m].onmessage = function(event) {//ワーカーから受け取り
            var Ps = event.data;
            var n = Ps.n; var l =Ps.l; var m =Ps.m;
            var Xs = Ps.x;
            var Ys = Ps.y;
            var Zs = Ps.z;
            var mat = new THREE.ParticleBasicMaterial({vertexColors:true, size: p_size});
            var pointGeos = new Array(3);
            for(var i=0; i<=2; i++) pointGeos[i] = new THREE.Geometry();
            if(m==0){
              for (var i=0; i< Zs.length; i++) {
                pointGeos[0].vertices.push(new THREE.Vertex( new THREE.Vector3(Zs[i].x, Zs[i].y, Zs[i].z) ));
                if(Zs[i].a >0 ) pointGeos[0].colors.push(new THREE.Color(0xff0000));
                else  pointGeos[0].colors.push(new THREE.Color(0x0000ff));
              }
            }else{
              for (var i=0; i< Xs.length; i++) {  
                pointGeos[1].vertices.push(new THREE.Vertex( new THREE.Vector3(Xs[i].x, Xs[i].y, Xs[i].z) ));
                if(Xs[i].a >0 ) pointGeos[1].colors.push(new THREE.Color(0xff0000));
                else  pointGeos[1].colors.push(new THREE.Color(0x0000ff));
                pointGeos[2].vertices.push(new THREE.Vertex( new THREE.Vector3(Ys[i].x, Ys[i].y, Ys[i].z) ));
                if(Ys[i].a >0 ) pointGeos[2].colors.push(new THREE.Color(0xff0000));
                else  pointGeos[2].colors.push(new THREE.Color(0x0000ff));
              }
            }

            if(m==0){
              scatterPlots[n][l][m][0].add(new THREE.ParticleSystem(pointGeos[0], mat));
               $id("s" + n + l + m ).innerHTML = "準備完了！" ;
              $id("n" + n + l + m ).style.display = 'inline';
             }else{
              scatterPlots[n][l][m][1].add(new THREE.ParticleSystem(pointGeos[1], mat));
               $id("s" + n + l + m + "x").innerHTML = "準備完了！" ;
              $id("n" + n + l + m + "x").style.display = 'inline';
              scatterPlots[n][l][m][2].add(new THREE.ParticleSystem(pointGeos[2], mat));
               $id("s" + n + l + m + "y").innerHTML = "準備完了！" ;
              $id("n" + n + l + m + "y").style.display = 'inline';
             }
             
          }
          if(m==0){
            $id("n" + n + l + m ).checked = false;
            $id("n" + n + l + m ).style.display = 'none';
          }else{
            $id("n" + n + l + m + "x").checked = false;
            $id("n" + n + l + m + "x").style.display = 'none';
            $id("n" + n + l + m + "y").checked = false;
            $id("n" + n + l + m + "y").style.display = 'none';
          }
        }
      }
    }
  }

  var width, height;
  var renderer;
  function initThree() {
    width = document.getElementById('canvas-frame').clientWidth;
    height = document.getElementById('canvas-frame').clientHeight;  
    try {renderer = new THREE.WebGLRenderer({antialias: true});} catch (e) {}  
    if(!renderer) document.getElementById("errer").innerHTML = '<p style="text-align:center;font-size:small; color:red">お使いの環境ではWebGLはご利用いただけません。<br />WebGLに対応していない方のためにGIFファイルを以下に用意しました。<br /><br /><img src="http://www.natural-science.or.jp/images/tutorial6.gif" alt="WEBGLデモ" /></p>';
    renderer.setSize(width, height);
    document.getElementById('canvas-frame').appendChild(renderer.domElement);
    renderer.setClearColorHex(0x000000, 1.0);
    $id("pn").value = p_max;
    $id("ps").value = p_size;      
  }
  
  var camera;
  var cameraL = 150;
  var cameraTheta = Math.PI*(1/2-0.01);
  var cameraPhi   = Math.PI*(3/2-0.01);  
  function initCamera() {  
    camera = new THREE.PerspectiveCamera( 45 , width / height , 1 , 10000 );
    camera.up.x = 0;
    camera.up.y = 0;
    camera.up.z = 1;
    camera.position.set(cameraL*Math.sin(cameraTheta)*Math.cos(cameraPhi),
              cameraL*Math.sin(cameraTheta)*Math.sin(cameraPhi),
              cameraL*Math.cos(cameraTheta));       
  }
  var scene;
  function initScene() {    
    scene = new THREE.Scene();
    scene.fog = new THREE.FogExp2( 0xFFFFFF, 0.0015 );    
  }
  var light, light2;
  function initLight() {
    light = new THREE.DirectionalLight(0xFFFFFF, 1.0, 0);
    light.position.set( 100, 100, 100 );
    scene.add(light);

    light2 = new THREE.AmbientLight(0x777777);
    scene.add(light2);
  }


  
  var scatterPlot;
  var axis;
  function initObject(){
    axis = new THREE.Object3D();
    scene.add(axis);
    scatterPlot = scatterPlots[1][0][0];
  
    function v(x,y,z){ return new THREE.Vertex(new THREE.Vector3(x,y,z)); }
    var lineGeo = new THREE.Geometry();
    lineGeo.vertices.push(
      v(-L/2, 0, 0), v(L/2, 0, 0),
      v(0, -L/2, 0), v(0, L/2, 0),
      v(0, 0, -L/2), v(0, 0, L/2),
    
      v(-L/2, L/2, -L/2), v(L/2, L/2, -L/2),
      v(-L/2, -L/2, -L/2), v(L/2, -L/2, -L/2),
      v(-L/2, L/2, L/2), v(L/2, L/2, L/2),
      v(-L/2, -L/2, L/2), v(L/2, -L/2, L/2),
    
      v(-L/2, 0, L/2), v(L/2, 0, L/2),
      v(-L/2, 0, -L/2), v(L/2, 0, -L/2),
      v(-L/2, L/2, 0), v(L/2, L/2, 0),
      v(-L/2, -L/2, 0), v(L/2, -L/2, 0),
    
      v(L/2, -L/2, -L/2), v(L/2, L/2, -L/2),
      v(-L/2, -L/2, -L/2), v(-L/2, L/2, -L/2),
      v(L/2, -L/2, L/2), v(L/2, L/2, L/2),
      v(-L/2, -L/2, L/2), v(-L/2, L/2, L/2),
    
      v(0, -L/2, L/2), v(0, L/2, L/2),
      v(0, -L/2, -L/2), v(0, L/2, -L/2),
      v(L/2, -L/2, 0), v(L/2, L/2, 0),
      v(-L/2, -L/2, 0), v(-L/2, L/2, 0),
    
      v(L/2, L/2, -L/2), v(L/2, L/2, L/2),
      v(L/2, -L/2, -L/2), v(L/2, -L/2, L/2),
      v(-L/2, L/2, -L/2), v(-L/2, L/2, L/2),
      v(-L/2, -L/2, -L/2), v(-L/2, -L/2, L/2),
    
      v(-L/2, 0, -L/2), v(-L/2, 0, L/2),
      v(L/2, 0, -L/2), v(L/2, 0, L/2),
      v(0, L/2, -L/2), v(0, L/2, L/2),
      v(0, -L/2, -L/2), v(0, -L/2, L/2)
    );
    var lineMat = new THREE.LineBasicMaterial({color: 0x444444, lineWidth: 1});
    var line = new THREE.Line(lineGeo, lineMat);
    line.type = THREE.Lines;
    axis.add(line);
    
    var titleX = createText2D('-X', 'gray');
    titleX.position.x = -(L/2+5);
    titleX.rotation.x = Math.PI/2; 
    axis.add(titleX);
    
    var titleX = createText2D('X', 'gray');
    titleX.position.x = (L/2+5);
    titleX.rotation.x = Math.PI/2;
    axis.add(titleX);
    
    var titleX = createText2D('-Y', 'gray');
    titleX.position.y = -(L/2+5);
    titleX.rotation.x = Math.PI/2;
    axis.add(titleX);
    
    var titleX = createText2D('Y', 'gray');
    titleX.position.y = (L/2+5);
    titleX.rotation.x = Math.PI/2;
    axis.add(titleX);
    
    var titleX = createText2D('-Z', 'gray');
    titleX.position.z = -(L/2+5);
    titleX.rotation.x = Math.PI/2;
    axis.add(titleX);
    
    var titleX = createText2D('Z', 'gray');
    titleX.position.z = (L/2+5);
    titleX.rotation.x = Math.PI/2;
    axis.add(titleX);
    
    start(1, 0, 0);//n=1だけデフォルトで計算スタート
    $id("n100").checked = true;    
    /*
    var AA = {n:1, l:0, m:0, p_max:p_max, L: L};
      workers[1][0][0].postMessage(AA);     // ワーカに数値を渡す
    $id("b100").innerHTML = "再計算";  ;    
    $id("s100").innerHTML = "計算中..." ;
    */    
  }
  function start(n, l, m) {//計算開始ボタンを押した時に呼び出される関数
    for(var i=0; i<=2; i++) {
      scene.remove( scatterPlots[n][l][m][i]);
      scatterPlots[n][l][m][i] = new THREE.Object3D();
    }
    p_max = parseInt($id("pn").value);
    p_size = parseFloat($id("ps").value);  
    $id("b" + n + l + m ).innerHTML = "再計算";  
    if(m==0){
      $id("s" + n + l + m).innerHTML = "計算中..." ;
    }else{
      $id("s" + n + l + m + "x").innerHTML = "計算中..." ;
      $id("s" + n + l + m + "y").innerHTML = "計算中..." ;
    }  
    var AA = {n:n, l:l, m:m, p_max:p_max, L: L};
    workers[n][l][m].postMessage(AA);     // ワーカに数値を渡す
  }

  function initEvent(){//イベントの登録
    window.addEventListener("mousedown", onMousedown, false);
    window.addEventListener("mouseup", onMouseup, false);
    window.addEventListener("mousemove",  onMousemove, false);
    window.addEventListener("mousewheel", onMousewheel, false);
    window.addEventListener('DOMMouseScroll', onMousewheel, false); //Firefox用（マウスホイール）
    window.addEventListener("dragover", onCancel, false);
    window.addEventListener("dragenter", onCancel, false);
    window.addEventListener("drop", onDropFile, false);
    
    for (var n = 1; n <= n_max; n++)
      for (var l = 0; l < n; l++)
        for (var m = 0; m <= l; m++)
        //$id("b" + n + l + m).addEventListener("click", start(n,l,m), false); //これでは、start(n,l,m)が実行されてしまうのでダメ
        //$id("b" + n + l + m).addEventListener("click", function(event) { start(n,l,m); }, false); //これでは、イベントの登録がfor文の後になるため、意図通り引き数を与えることができないダメ
        $id("b" + n + l + m).addEventListener("click", (function (n_, l_, m_) { return function() { start(n_, l_, m_); } })(n, l, m) , false);
    //参考ページ
    //http://d.hatena.ne.jp/Syunpei/20070605/1181035316
    //http://d.hatena.ne.jp/uriyuri/20081014/1223974862
  }

  function loop() {
    for (var n = 1; n <= n_max; n++)
      for (var l = 0; l < n; l++)
        for (var m = 0; m <= l; m++){
          if(m==0){
            if($id("n" + n + l + m).checked) scene.add(scatterPlots[n][l][m][0]);
            else scene.remove( scatterPlots[n][l][m][0]);            
          }else{
            if($id("n" + n + l + m + "x").checked) scene.add(scatterPlots[n][l][m][1]);
            else scene.remove( scatterPlots[n][l][m][1]);
            if($id("n" + n + l + m + "y").checked) scene.add(scatterPlots[n][l][m][2]);
            else scene.remove( scatterPlots[n][l][m][2]);                    
          }
          
        }

    renderer.clear();
    camera.lookAt( {x:0, y:0, z:0 } );    
    renderer.render(scene, camera);
    window.requestAnimationFrame(loop);
  }
  function threeStart() {
    initEvent();
    initThree();
    initCamera();
    initScene();    
    initLight();  
    initObject();
    loop();
  }
  function createTextCanvas(text, color, font, size) {
    size = size || 24;
    var canvas = document.createElement('canvas');
    var ctx = canvas.getContext('2d');
    var fontStr = (size + 'px ') + (font || 'Arial');
    ctx.font = fontStr;
    var w = ctx.measureText(text).width;
    var h = Math.ceil(size);
    canvas.width = w;
    canvas.height = h;
    ctx.font = fontStr;
    ctx.fillStyle = color || 'black';
    ctx.fillText(text, 0, Math.ceil(size*0.8));
    return canvas;
  }
  
  function createText2D(text, color, font, size, segW, segH) {
    var canvas = createTextCanvas(text, color, font, size);
    var plane = new THREE.PlaneGeometry(canvas.width, canvas.height, segW, segH);
    var tex = new THREE.Texture(canvas);
    tex.needsUpdate = true;
    var planeMat = new THREE.MeshBasicMaterial({
      map: tex, color: 0xffffff, transparent: true
    });
    var mesh = new THREE.Mesh(plane, planeMat);
    mesh.scale.set(0.15, 0.15, 0.15);
    mesh.doubleSided = true;
    return mesh;
  }
  function QuaternionRotation(theta, u, v){ //(回転角, 回転軸, 任意のベクトル)
    var P = new quat4.create([v[0],v[1],v[2],0]);
    var Q = new quat4.create([-u[0]*Math.sin(theta/2), -u[1]*Math.sin(theta/2), -u[2]*Math.sin(theta/2), Math.cos(theta/2)]);
    var R = new quat4.create([u[0]*Math.sin(theta/2), u[1]*Math.sin(theta/2), u[2]*Math.sin(theta/2), Math.cos(theta/2)]);
    var S0 = quat4.multiply(P,Q, quat4.create());
    var S =  quat4.multiply(R,S0,quat4.create());  
    return S;
  }


////マウスイベント////////////////////////////////////////////////////
  var down = false;
  var v, u, w, theta;
  function onMousedown (ev){  //マウスダウン時イベント
    if (ev.target == renderer.domElement) { 
      down = true;
      sx = ev.clientX; sz = ev.clientY;
      v = new vec3.create([camera.position.x,camera.position.y,camera.position.z]);  //任意の点
      u = new vec3.create([-v[0]*v[2],-v[1]*v[2], (v[0]*v[0]+v[1]*v[1])]);
      u = vec3.normalize(u, vec3.create());      
      w = new vec3.create([v[1],-v[0],0]);
      w = vec3.normalize(w, vec3.create());
      
    }
  };
  function onMouseup (){       //マウスアップ時イベント
    down = false; 
  };
  function onMousemove (ev) {  //マウスムーブ時イベント
    if (down) {
      if (ev.target == renderer.domElement) {
        var dx = -(ev.clientX - sx);
        var dz = -(ev.clientY - sz);

        theta =  dx/ 100;
        var S = QuaternionRotation(theta, u, [camera.position.x,camera.position.y,camera.position.z]);        
        theta =  -dz/ 100;
        S =  QuaternionRotation(theta, w, [S[0],S[1],S[2]]);        
        camera.position.set(S[0],S[1],S[2]);  
        sx -= dx;
        sz -= dz;  
      }
    }
  }
  function onMousewheel(ev){//マウスホイール時イベント
    var x = camera.position.x;
    var y = camera.position.y;
    var z = camera.position.z;
    cameraL = Math.sqrt(Math.pow(x,2)+Math.pow(y,2)+Math.pow(z,2));
    cameraTheta = Math.acos(z/cameraL);
    if( y >= 0 ) cameraPhi = Math.acos(x/(cameraL*Math.sin(cameraTheta)));
    else cameraPhi = 2.0*Math.PI - Math.acos(x/(cameraL*Math.sin(cameraTheta)));

    var delta;//回転量
    if (ev.wheelDelta) { 
      delta = ev.wheelDelta; //Chrome用
    } else if (ev.detail) {
      delta = -ev.detail*20;      //Firefox用
    }
    cameraL += delta * 0.2;
    if(cameraL < 0) cameraL = 0.1;
    camera.position.set(cameraL*Math.sin(cameraTheta)*Math.cos(cameraPhi),
              cameraL*Math.sin(cameraTheta)*Math.sin(cameraPhi),
              cameraL*Math.cos(cameraTheta));
  }
  var onDropFile = function(ev){         // ファイルドロップ時イベント
    ev.preventDefault();
    var file = ev.dataTransfer.files[0]; // File オブジェクトを取得
    readFile(file);                     // ファイル読み込み
  };
  var onCancel = function(ev){            // デフォル処理をキャンセル
    if(ev.preventDefault) { ev.preventDefault(); }
    return false;
  };
  function f_write(){
    var  str = "";

    for (var i = 0; i < N_EC; i++) {
      if(!ECs[i].flag) continue;
      for (var j = 0; j < n_line; j++) {
        var geometry = new THREE.Geometry();
        for (var k = 0; k < n_step; k++) {
          if(Lines[i][j][k] != undefined && Lines[i][j][k] != undefined && Lines[i][j][k] != undefined)
            str  +=  Lines[i][j][k].x  + " " + Lines[i][j][k].y  + " " + Lines[i][j][k].z  + "\n";
          else break;
        }
        str  += "\n";
      }
    }
    var blobBuilder;
    if ("MozBlobBuilder" in window) {
      blobBuilder = new MozBlobBuilder();
    } else if ("WebKitBlobBuilder" in window) {
      blobBuilder = new WebKitBlobBuilder();
    }
    blobBuilder.append(str);
    //var disp = document.getElementById("download");
    if (window.URL) {
      window.open(window.URL.createObjectURL(blobBuilder.getBlob()) , "New Window", "");
    } else if (window.webkitURL) {
      window.open(window.webkitURL.createObjectURL(blobBuilder.getBlob()), "New Window", "");          
    }
    //disp.innerHTML = 'ファイルがダウンロードされました （t='+ t +'）';
  }  
///////////////////////////////////////////////////////////////////////
window.onload = function(){
  init();
  threeStart();
}

WebWorker（worker_wave.js）

// WebWorker
onmessage = function(event) {
    var AA = event.data;
  var results = wavefunction(AA);
    // 生成元に結果を返す
    results.n = AA.n; //主量子数
    results.l = AA.l; //方位量子数
    results.m = AA.m; //磁気量子数 m = 0 ～ l
    postMessage(results);
}
function wavefunction(AA){
  var n = AA.n; //主量子数
    var l = AA.l; //方位量子数
    var m = AA.m; //磁気量子数 m = 0 ～ l
  var L = AA.L; //計算する領域のサイズ
  var p_max = AA.p_max; //描画する点の数
  var results = {};
  var points = new Array(); 
  points[0] = new Array();
  if(m>0){
    points[1] = new Array();
    points[2] = new Array();
  }
  if(n==1){
    times  = 5;
    timesL = L/3;
  }
  else if(n==2){
    times  = 20;
    timesL = L/2;    
  }
  else if (n==3){
    times  = 50;
    timesL = L/1.5;        
  }
  else if (n==4){
    times =70;
    timesL = L;      
  }
  //var mat = new THREE.ParticleBasicMaterial({vertexColors:true, size: p_size});
  var pointCount = p_max*100;
  //var pointGeo = new THREE.Geometry();
  var p=0;
  for (var i=0; i<pointCount; i++) {
    var x = timesL/2* (Math.random() - Math.random());
    var y = timesL/2* (Math.random() - Math.random());
    var z = timesL/2* (Math.random() - Math.random());
    
    var r = Math.sqrt(Math.pow(x,2)+Math.pow(y,2)+Math.pow(z,2));
    var theta = Math.acos(z/r);
    var phi;
    if(y>=0) phi = Math.acos(x/(r*Math.sin(theta)));
    else phi = 2.0*Math.PI - Math.acos(x/(r*Math.sin(theta)));
    if(r==0){
      theta = 0;
      phi = 0;
    }
    var R = 2.0/Math.pow(n,2) * Math.sqrt(Factorial(n-l-1)/Factorial(n+l)) * Math.exp(-r/n) * Math.pow( 2.0*r/n,l) *Laguerre(2*l+1, n-l-1, 2.0*r/n)  ;
    var Y = Math.pow(-1.0, m) * Math.sqrt(l+1.0/2.0) * Factorial(l-m)/Factorial(l+m) * Legendre(m,l,Math.cos(theta));
    var Psi, Psi_x, Psi_y;

    Psi = R * Y;
    if(Math.abs(Psi) * times  <Math.random()) continue;  
    if(m==0) {
      if(Psi>0) points[0].push({x:x,y:y,z:z,a:1});
      else points[0].push({x:x,y:y,z:z,a:-1});
    }else{
      var Yx = Y * Math.cos(m*phi);
      var Yy = Y * Math.sin(m*phi);
      Psi_x = R * Yx;
      Psi_y = R * Yy;
      if(Psi_x>0) points[1].push({x:x,y:y,z:z,a:1});
      else points[1].push({x:x,y:y,z:z,a:-1});
      if(Psi_y>0) points[2].push({x:x,y:y,z:z,a:1});
      else points[2].push({x:x,y:y,z:z,a:-1});      
    } 
    p++;
    if(p > p_max) break;
  }
  if(m==0) {  
    results.z = points[0];
  }else{
    results.x = points[1];  
    results.y = points[2];
  }
  return results;
}
  function Factorial(n, n1) //
  {
  　　var m = n1 || 1; 
    if( n<=0 ) return (1.0);
    var F = 1.0;
    for(var i=n; i>=2; i-=m ){
      F *= i;    
    }
    return (F);
  }
  function Legendre (m, l, x ) {//ルジャンドル陪関数
    var mm = Math.abs(m);
    if( mm>l )  return (0);
    var r0, r1, r2;
      r0 = 0.0;
      r1 = Math.pow(1.0-x*x, mm/2.0) * Factorial(2*mm-1,2);
      if( mm==l && m>=0) return (r1);
      if( mm==l && m<0)  return (r1 * Math.pow(-1.0,mm) * Factorial(l-mm)/Factorial(l+mm)) ;
      for(var ll = mm+1; ll<=l; ll++ ){
        r2 = ((2.0*ll-1.0)*x*r1 - (ll+mm-1.0)*r0)/(ll-mm);
        r0 = r1;
        r1 = r2;
      }
    if(m>=0) return (r2);
    else return (r2 * Math.pow(-1.0,mm) * Factorial(l-mm)/Factorial(l+mm)) ;
  }
  function Laguerre(k, n, x){
    var sum=0;
    for(var m=0; m<=n; m++){
      sum += Math.pow(-x,m)*Factorial(n+k)/Factorial(n-m)/Factorial(k+m)/Factorial(m);
    }
    return sum;
  }

C言語

図を描画用にデータ出力用のプログラムです。

/*
水素原子の波動関数（厳密解）
(2012.03.29 公開)
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
double Factorial(int n);
double Factorial(int n, int m);
const int n_max = 4;
const int kizami = 200;
const double L = 80.0;
double Laguerre( int k, int n, double x);           //ラゲール陪関数
double Legendre( int m, int l, double x);           //ルジャンドル陪関数

string folder = "Hydrogen";//作成するフォルダ名


int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(8);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif
  double r_min = 0.0;
  double r_max =  40.0;
  const int Z = 1;

  /*// 動径分布関数
  for(int n=1; n<=n_max; n++)
  {
    for(int l=0; l<n; l++)
    {
      for(int m=-l; m<=l; m++)
      {
        char str[200];
        string str1;
        ofstream fout_s;
        sprintf(str, "/R%d_%d_%d.data", n, l, m); str1 = folder + str; //動径方向
        fout_s.open(str1.c_str());
        for(int i=0; i<=kizami*100; i++)
        {
          double x = r_min + (r_max-r_min)/double(kizami*100)*double(i);
          double R = 2.0/pow(double(n),2) * sqrt(Factorial(n-l-1)/Factorial(n+l)) * exp(-x/double(n)) * pow( 2.0*x/double(n),l) *Laguerre(2*l+1, n-l-1, 2.0*x/double(n))  ;
          fout_s << x << " " << R << endl;
        }
        fout_s.close();
      }
    }
  }
*/
  for(int n=1; n<=n_max; n++)
  {
    for(int l=0; l<n; l++)
    {
      for(int m=0; m<=l; m++)
      {
        char str[200];
        string str1;
        ofstream fout_s;
        sprintf(str, "/Psi%d_%d_%d.data", n, l, m); str1 = folder + str; //
        fout_s.open(str1.c_str());
        for(int ix=0; ix<=kizami; ix++ )
        {
          for(int iy=0; iy<=kizami; iy++ )
          {
            double x = - L/2.0 + L * double(ix)/double(kizami);
            double y = - L/2.0 + L * double(iy)/double(kizami);
            double z =0;
            double r = sqrt(pow(x,2)+pow(y,2)+pow(z,2));
            double theta = acos(z/r);
            double phi;
            if(y>=0) phi = acos(x/r);
            else phi = 2.0*PI - acos(x/r);
            if(r==0){
              theta = 0;
              phi = 0;
            }
            double R = 2.0/pow(double(n),2) * sqrt(Factorial(n-l-1)/Factorial(n+l)) * exp(-r/double(n)) * pow( 2.0*r/double(n),l) *Laguerre(2*l+1, n-l-1, 2.0*r/double(n))  ;
            double Y = pow(-1.0, m) * sqrt(double(l)+1.0/2.0) * Factorial(l-m)/Factorial(l+m) * Legendre(m,l,cos(theta));
            if(m==0) {
              fout_s << x << " " << y << " "  << R * Y << endl;
            }else{
              double Yx = Y * cos(double(m)*phi);
              double Yy = Y * sin(double(m)*phi);
              fout_s << x << " " << y << " "  << R * Yx << " " << R * Yy << endl ;
            }
          }
          fout_s << "" << endl;
        }
        fout_s.close();
      }
    }
  }
}
double Laguerre( int k, int n, double x)
{
  double sum=0;
  for(int m=0; m<=n; m++){
    sum += pow(-x,m)*Factorial(n+k)/Factorial(n-m)/Factorial(k+m)/Factorial(m);
  }
  return sum;
}
double Legendre( int m, int l, double x)
{
  int mm = abs(m);
  if( mm>l )  return 0;
  double r0, r1, r2;
    r0 = 0.0;
    r1 = pow(1.0-x*x, double(mm)/2.0) * Factorial(2*mm-1, 2);
    if( mm==l && m>=0) return r1;
    if( mm==l && m<0)  return r1 * pow(-1.0,mm) * Factorial(l-mm)/Factorial(l+mm) ;
    for(int ll = mm+1; ll<=l; ll++ ){
      r2 = ((2.0*ll-1.0)*x*r1 - (ll+mm-1.0)*r0)/(ll-mm);
      r0 = r1;
      r1 = r2;
    }
  if(m>=0) return r2;
  else return r2 * pow(-1.0,mm) * Factorial(l-mm)/Factorial(l+mm) ;
}
double Factorial(int n)
{
  if( n<=0 ) return 1.0;
  double F = 1.0;
  for(int i=n; i>=2; i--){
    F *= double(i);    
  }
  return F;
}
double Factorial(int n, int m)
{
  if( n<=0 ) return 1.0;
  double F = 1.0;
  for(int i=n; i>=2; i=i-m){
    F *= double(i);    
  }
  return F;
}

gnuplotテンプレート

上のプログラムで出力したデータを用いて、gif描画用のgnuplotテンプレートです。

set pm3d                           ## 3次元カラー表示
set pm3d map                       ## カラーマップ表示
set pm3d interpolate 5, 5          ## 補間
set ticslevel 10

set nokey
set tics font 'Times,14'
set size square

########################################################
## gif ファイル出力の場合 ##############################
########################################################
set terminal gif optimize size 600, 480
cb = 1                  ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")
L=5.2
set xr[-L:L]            ##<---------描画x軸の範囲
set yr[-L:L]            ##<---------描画y軸の範囲

set output 'Psi1_0_0.gif'
splot "Psi1_0_0.data" u 1:2:3 with pm3d

L=10                    
set xr[-L:L]            ##<---------描画x軸の範囲
set yr[-L:L]            ##<---------描画y軸の範囲
cb = 0.2                ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")

set output 'Psi2_0_0.gif'
splot "Psi2_0_0.data" u 1:2:3 with pm3d

cb = 0.1                ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")

set output 'Psi2_1_0.gif'
splot "Psi2_1_0.data" u 1:2:3 with pm3d

set output 'Psi2_1_x.gif'
splot "Psi2_1_1.data" u 1:2:3 with pm3d

set output 'Psi2_1_y.gif'
splot "Psi2_1_1.data" u 1:2:4 with pm3d

cb = 0.03               ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")
L=20
set xr[-L:L]            ##<---------描画x軸の範囲
set yr[-L:L]            ##<---------描画y軸の範囲

set output 'Psi3_0_0.gif'
splot "Psi3_0_0.data" u 1:2:3 with pm3d

set output 'Psi3_1_0.gif'
splot "Psi3_1_0.data" u 1:2:3 with pm3d

set output 'Psi3_1_x.gif'
splot "Psi3_1_1.data" u 1:2:3 with pm3d

set output 'Psi3_1_y.gif'
splot "Psi3_1_1.data" u 1:2:4 with pm3d


set output 'Psi3_2_0.gif'
splot "Psi3_2_0.data" u 1:2:3 with pm3d

cb = 0.01               ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")

set output 'Psi3_2_x.gif'
splot "Psi3_2_1.data" u 1:2:3 with pm3d

set output 'Psi3_2_y.gif'
splot "Psi3_2_1.data" u 1:2:4 with pm3d

set output 'Psi3_2_2x.gif'
splot "Psi3_2_2.data" u 1:2:3 with pm3d

set output 'Psi3_2_2y.gif'
splot "Psi3_2_2.data" u 1:2:4 with pm3d


L=30
set xr[-L:L]            ##<---------描画x軸の範囲
set yr[-L:L]            ##<---------描画y軸の範囲

cb = 0.02               ##<---------カラーバーの指定
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")

set output 'Psi4_0_0.gif'
splot "Psi4_0_0.data" u 1:2:3 with pm3d

set output 'Psi4_1_0.gif'
splot "Psi4_1_0.data" u 1:2:3 with pm3d

set output 'Psi4_1_x.gif'
splot "Psi4_1_1.data" u 1:2:3 with pm3d

set output 'Psi4_1_y.gif'
splot "Psi4_1_1.data" u 1:2:4 with pm3d

set output 'Psi4_2_0.gif'
splot "Psi4_2_0.data" u 1:2:3 with pm3d

cb = 0.005
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")

set output 'Psi4_2_x.gif'
splot "Psi4_2_1.data" u 1:2:3 with pm3d

set output 'Psi4_2_y.gif'
splot "Psi4_2_1.data" u 1:2:4 with pm3d

set output 'Psi4_2_2x.gif'
splot "Psi4_2_2.data" u 1:2:3 with pm3d

set output 'Psi4_2_2y.gif'
splot "Psi4_2_2.data" u 1:2:4 with pm3d


L=40
set xr[-L:L]            ##<---------描画x軸の範囲
set yr[-L:L]            ##<---------描画y軸の範囲

set output 'Psi4_3_0.gif'
splot "Psi4_3_0.data" u 1:2:3 with pm3d

set output 'Psi4_3_x.gif'
splot "Psi4_3_1.data" u 1:2:3 with pm3d

set output 'Psi4_3_y.gif'
splot "Psi4_3_1.data" u 1:2:4 with pm3d


cb = 0.001
set cbrange[-cb:cb]
set palette defined ( -cb "blue" , 0 "black", cb "red")


set output 'Psi4_3_2x.gif'
splot "Psi4_3_2.data" u 1:2:3 with pm3d

set output 'Psi4_3_2y.gif'
splot "Psi4_3_2.data" u 1:2:4 with pm3d

set output 'Psi4_3_3x.gif'
splot "Psi4_3_3.data" u 1:2:3 with pm3d

set output 'Psi4_3_3y.gif'
splot "Psi4_3_3.data" u 1:2:4 with pm3d

・C++言語
・gnuplotテンプレート
・イラストレータ

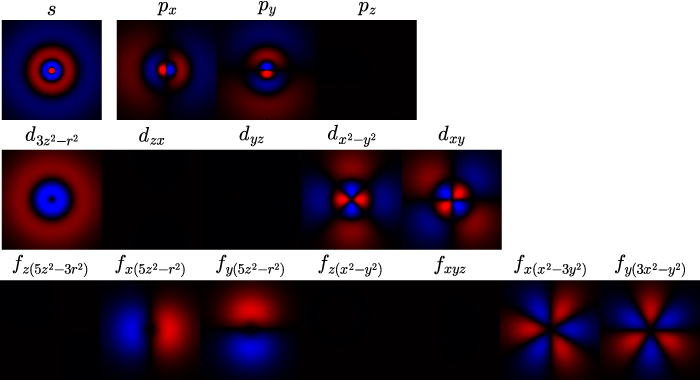
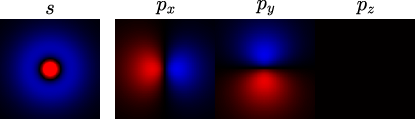
計算結果

上のgnuplot テンプレートで出力した gif データです。 $\,z=0$ の平面での波動関数の振幅に比例する確率分布による点描画です。

	MEMSパークコンソーシアム設立20周年記念シンポジウムにおいて「国際イノベーションコンテスト」世界１位入賞アプリを展示しました 2024.12.29 【大草芳江｜TOPICS】
	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】

HTML5による物理シミュレーション環境の構築
水素原子の波動関数ビューア

計算アルゴリズム

スクリーンショット

プログラムソース

Javascript

本体

WebWorker（worker_wave.js）

C言語

gnuplotテンプレート

計算結果

主量子数： $\,n=1$ （K殻）

主量子数： $\,n=2$ （L殻）

主量子数： $\,n=3$ （M殻）

主量子数： $\,n=4$ （N殻）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

HTML5による物理シミュレーション環境の構築水素原子の波動関数ビューア

計算アルゴリズム

スクリーンショット

プログラムソース

Javascript

本体

WebWorker（worker_wave.js）

C言語

gnuplotテンプレート

計算結果

主量子数：（K殻）

主量子数：（L殻）

主量子数：（M殻）

主量子数：（N殻）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

HTML5による物理シミュレーション環境の構築
水素原子の波動関数ビューア

主量子数： $\,n=1$ （K殻）

主量子数： $\,n=2$ （L殻）

主量子数： $\,n=3$ （M殻）

主量子数： $\,n=4$ （N殻）