高速フーリエ変換のテスト（矩形関数）

有限区間のフーリエ変換

の範囲で定義される実関数 を正規直交系を成す三角関数の和で表される指数関数を用いて、次の通りに展開することを考えます。

展開係数は一般的に複素数です。 展開係数は指数関数の完全性から、元の関数から一意に

と与えられます。これはフーリエ級数展開と呼ばれ、もとの関数が空間分布であれば波数成分が、時間分布であれば周波数成分を取得することができます。 展開係数の実部を虚部をそれぞれ と表したとき、元の関数が偶関数の場合はのみ値を持ち となり、反対に元の関数が奇関数の場合はのみ値を持ちとなります。また、が実関数の場合には、

が一般的に成り立ちます。なお、Nが∞の極限で元の関数を完全に再現しますが、数値計算の場合には必要となる計算精度に応じて与えます。この展開係数を高速に計算するのが高速フーリエ変換（FFT）です。 また、展開係数から元の関数を計算するのは逆フーリエ変換と呼ばれ、ほとんど同じ計算で得ることができます。

高速フーリエ変換の例：矩形関数

の範囲で定義される実関数の例として矩形関数

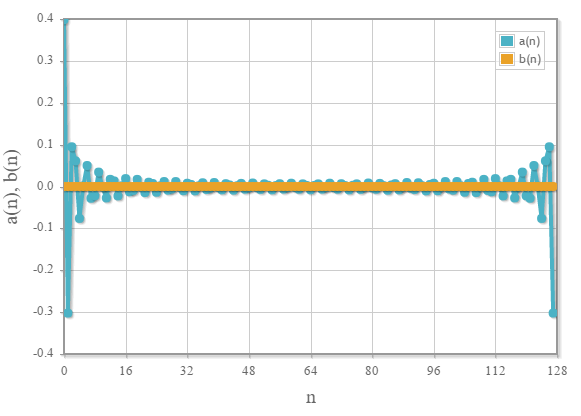
の展開係数を高速フーリエ変換を用いて計算します。は矩形の幅を表します。 以下の結果はN=128の場合（２のべきである必要があります）です。元の関数が偶関数なのでのみ値を持っていることが確認できます。

展開係数

※実物は画像をクリックするとご覧いただけます。

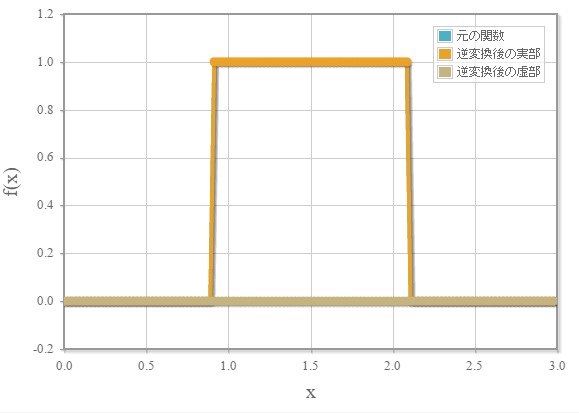
逆フーリエ変換

上記で計算した展開系数を用いて逆フーリエ変換を行って元の関数を再現した結果です。元の矩形関数をほぼ再現していることがわかります。

※実物は画像をクリックするとご覧いただけます。

実装方法

高速フーリエ変換用の関数は次のとおりです。

//高速フーリエ変換
function FFT( an, bn, N, Inverse ){
	/////////////////////////////////////////
	//参考：Javaで学ぶシミュレーションの基礎
	/////////////////////////////////////////
	// 入力
	// N  ： 項数（2のべき乗）
	// an : 実数配列（順変換：実数空間データを項数Nで指定、逆変換：展開係数a(n)）
	// bn : 実数配列（順変換：虚数空間データを項数Nで指定、逆変換：展開係数b(n)）
	// Inverse : 逆変換の場合に true
	/////////////////////////////////////////
	// 出力
	// an : 実数配列（順変換：展開係数a(n)、逆変換：実数空間データ）
	// bn : 実数配列（順変換：展開係数b(n)、逆変換：虚数空間データ）
    /////////////////////////////////////////

	var ff = Inverse ? 1 : -1;

	var rot = new Array(N);
	for( var i = 0; i < rot.length; i++ ) rot[ i ] = 0;

	var nhalf = N/2, num = N/2;
	var sc = 2 * Math.PI / N;

	while( num >= 1 ){

		for(var j = 0; j < N; j += 2 * num ){

			var phi = rot[j] / 2;
			var phi0 = phi + nhalf;
			var c = Math.cos( sc * phi );
			var s = Math.sin( sc * phi * ff );

			for( var k = j; k < j + num; k++ ){

				var k1 = k + num;
				var a0 = an[ k1 ] * c - bn[ k1 ] *s;
				var b0 = an[ k1 ] * s + bn[ k1 ] *c;
				an[ k1 ] = an[ k ] - a0;
				bn[ k1 ] = bn[ k ] - b0;
				an[ k ] = an[ k ] + a0;
				bn[ k ] = bn[ k ] + b0;
				rot[ k ] = phi;
				rot[ k1 ] = phi0;

			}

		}

		num = num / 2;

	}

	for( var i = 0; i < N ; i++ ){
		var j = rot[ i ]; 
		if( j > i ){

			var tmp = an[ i ];
			an[ i ] = an[ j ];
			an[ j ] = tmp;

			var tmp = bn[ i ];
			bn[ i ] = bn[ j ];
			bn[ j ] = tmp;	

		}
	}

	if( !Inverse ){
		for( var i = 0; i < N ; i++ ){

			an[ i ] = an[ i ] / N;
			bn[ i ] = bn[ i ] / N;

		}	
	}
}

元の関数から展開係数を計算するプログラムは次のとおりです。

//項数と空間距離
var N = 128;
var L = 3;
//元の関数
function f( x ){
//	return Math.sin( 2 * Math.PI / L * 2 * x );
	if( L/2-L/5 < x  &&  x < L/2+L/5 ) return 1;
	else return 0;
}
//展開係数
var an = []; 
var bn = [];
//空間
var _an = [];
var _bn = []; 

for( var i=0; i<N; i++ ){
	var x = L/N * i;
	an[ i ] = f( x );
	bn[ i ] = 0;
}
//変換の実行
FFT( an, bn, N );

FFT関数実行後、計算後の「an」「bn」に展開係数が格納されます。また、逆変換も同様の手続きです。

for( var n = 0; n < N; n++ ){
	_an[ n ] = an[ n ];
	_bn[ n ] = bn[ n ];
}
//逆変換の実行
FFT( _an, _bn, N, true);

以上です。