ゼロから作るDeep Learning
1n1型２層ニューラルネットワークで１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
文責：遠藤 理平 （2017年4月14日）
カテゴリ：ゼロから作るDeep Learning(49)
目次
- 準備１：行列の和と積を計算する関数の実装
- 準備２：ベクトルと行列の積を計算する関数の実装
- 準備３：多変数関数の数値微分と極小値の探索
- １．１層ニューラルネットワークの実装（バイアスなし、活性化関数なし、学習なし）
- ２．１層ニューラルネットワークへのバイアスと活性化関数の追加
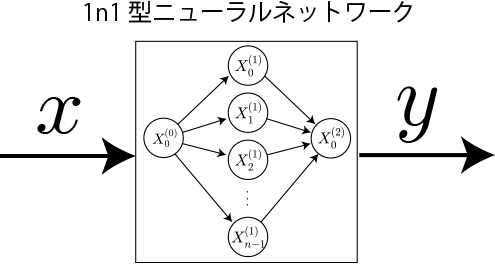
- ３．1n1型２層ニューラルネットワークの実装（学習なし）
- ４．１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム
- ５．１変数関数を学習させてみる２：勾配法による学習計算アルゴリズムの実装
- ６．１変数関数を学習させてみる３：ニューロン数による学習効果の違い
- ７．誤差逆伝搬法（バックプロパゲーション）の導出
- ８．順伝播型ニューラルネットワーク「FFNNクラス」の実装（JavaScript）
- ９．三角関数のサンプリング学習（WebWorkersによる並列計算）
- 10．学習後の各層ニューロンの重みの可視化
- 11．層数とニューロン数による学習効果の違い
学習のステップ
前項では勾配法による極小値探索の計算アルゴリズムを示しました。
本項では実際にニューラルネットワークで１変数関数を学習させてみましょう（入力値の範囲をとします）。必要なステップは次のとおりです。
（１）重みとバイアスにランダム値を与える ← 区間[-0.5, 0.5]をランダムで与える
（２）からランダムに取得した1個の入力値に対する損失関数値を計算する
（３）重みとバイアスに対する損失関数の勾配を計算する
（４）（２）と（３）をM回繰り返して勾配の平均を計算する ← このM個のサンプルのグループはミニバッチと呼ばれる。
（５）（４）で得られた平均勾配を用いて重みとバイアスの値を更新する ← この１回の値の更新はエポックと呼ばれる
（６）勾配を初期化する（０を与える）
（７）（２）から（６）の操作（エポック）をT回繰り返す
（８）から等間隔で取得した入力に対するニューラルネットワークの出力値を得て、元の関数と比較してみる。
１次関数、２次関数、３次関数を学習させてた結果
１次関数![f(x) = x \ , \ [0\leq x \leq 1]]()
１変数関数の最も簡単な例である１次関数を学習させた結果です。
初期パラメータがランダムに与えられていますので毎回結果が変化しますが、概ね学習回数300回程度で損失関数が極小値をとり、学習が完了していることがわかります。 学習後のニューラルネットワークの入力に対する出力は概ね元の関数上に乗っていることが確認できます。
２次関数![f(x) = x^2 \ , \ [0\leq x \leq 3]]()
次に曲線である２次関数についてです。デフォルトの学習率を0.03と先の１次関数の場合と比べて1/3の大きさとしました。今回は入力値の区間を広げたことでとりうる関数値の傾きが大きくなった結果、学習率が0.1ではうまく学習することができませんでした。
第１層ニューロン数:10、学習回数:1000、学習率:0.03で概ね元の関数を表現できています。
３次関数![f(x) = x^3-2.5x^2 \ , \ [0\leq x \leq 3]]()
最後に極小値をもつ３次関数についてです。デフォルトの学習回数を3000回としています。概ね表現できていることがわかります。
ニューラルネットワークを生成するNNクラスの拡張
前項で開発したNNクラスに上記のステップ（６）で示した勾配を格納する多重配列の初期化用メソッドを追加します。
//ニューラルネットワーク
var NN = function( W, B, h, sigma, eta ){
//重み
this.W = W;
//W.length : 層数
//W[].length : 列（後ニューロン数）
//W[][].length : 行（前ニューロン数）
//１ステップ前のWを保持する多重配列
this._W = [];
//バイアス
this.B = B;
this._B = [];
//偏微分値を格納する多重配列
this.dLdW = [];
this.dLdB = [];
//活性化関数
this.h = h;
this.sigma = sigma;
//ニューロンの初期化
this.X = [];
//学習効率
this.eta = eta || 0.1;
this.setup();
}
//各種プロパティの初期化
NN.prototype.setup = function( ){
////////////////////////////////////////////
// ニューロンの初期化
////////////////////////////////////////////
for( var i = 0; i < this.W.length; i++ ){
this.X[ i ] = [];
for( var j = 0; j < this.W[ i ][ 0 ].length; j++ ){
this.X[ i ][ j ] = 0;
}
}
//出力層
this.X[ this.W.length ] = [];
for( var j = 0; j < this.W[ this.W.length-1 ].length; j++ ){
this.X[ this.W.length ][ j ] = 0;
}
////////////////////////////////////////////
// 重み格納用多重配列と偏微分値格納多重配列の初期化
////////////////////////////////////////////
for( var i = 0; i < this.W.length; i++ ){
this._W[ i ] = [];
this.dLdW[ i ] = [];
for( var j = 0; j < this.W[ i ].length; j++ ){
this._W[ i ][ j ] = [];
this.dLdW[ i ][ j ] = [];
for( var k = 0; k < this.W[ i ][ j ].length; k++ ){
this._W[ i ][ j ][ k ] = this.W[ i ][ j ][ k ] ;
this.dLdW[ i ][ j ][ k ] = 0;
}
}
}
////////////////////////////////////////////
// バイアス格納用多重配列
////////////////////////////////////////////
for( var i = 0; i < this.B.length; i++ ){
this._B[ i ] = [];
this.dLdB[ i ] = [];
for( var j = 0; j < this.B[ i ].length; j++ ){
this._B[ i ][ j ] = this.B[ i ][ j ];
this.dLdB[ i ][ j ] = 0;
}
}
}
//重みによる勾配をリセット
NN.prototype.resetDLdW = function( ){
for( var i = 0; i < this.W.length; i++ ){
for( var j = 0; j < this.W[ i ].length; j++ ){
for( var k = 0; k < this.W[ i ][ j ].length; k++ ){
this.dLdW[ i ][ j ][ k ] = 0;
}
}
}
}
//バイアスによる勾配をリセット
NN.prototype.resetDLdB = function( ){
for( var i = 0; i < this.B.length; i++ ){
for( var j = 0; j < this.B[ i ].length; j++ ){
this.dLdB[ i ][ j ] = 0;
}
}
}
//入力層（０層目ニューロン値）へのインプット
NN.prototype.setInput = function( Input ){
for( var i = 0; i < Input.length; i++ ){
this.X[ 0 ][ i ] = Input[ i ];
}
}
//出力層へのアウトプット
NN.prototype.getOutput = function( ){
//各層ニューロン値の計算
for( var i = 0; i < this.W.length; i++ ){
this.multiplayMatrixVector ( this.W[ i ], this.X[ i ], this.X[ i+1 ] );
this.addVectors ( this.X[ i+1 ], this.B[ i ], this.X[ i+1 ] );
//活性化関数の実行
if( i < this.W.length-1 ){
//隠れ層
this.adoptAFh( this.X[ i+1 ], this.X[ i+1 ] );
} else {
//出力層
this.adoptAFsigma( this.X[ i+1 ], this.X[ i+1 ] );
}
}
return this.X[ this.X.length -1 ];
}
//行列×ベクトルの計算
NN.prototype.multiplayMatrixVector = function( M, V, C ){
C = C || [];
var Mgyou = M.length;
var Mretu = M[ 0 ].length;
for( var i = 0; i < Mgyou; i++ ){
C[ i ] =0;
for( var j = 0; j < Mretu; j++ ){
C[ i ] += M[ i ][ j ] * V[ j ];
}
}
return C;
}
//ベクトルの和
NN.prototype.addVectors = function( V1, V2, V3 ){
V3 = V3 || [];
for( var i = 0; i < V1.length; i++ ){
V3[ i ] = V1[ i ] + V2[ i ];
}
return V3;
}
//活性化関数の実行
NN.prototype.adoptAFh = function( V_in, V_out ){
V_out = V_out || [];
for( var i = 0; i < V_in.length; i++ ){
V_out[ i ] = this.h( V_in[ i ] );
}
return V_out;
}
NN.prototype.adoptAFsigma = function( V_in, V_out ){
V_out = V_out || [];
for( var i = 0; i < V_in.length; i++ ){
V_out[ i ] = this.sigma( V_in[ i ] );
}
return V_out;
}
実行方法
NNクラスを用いて１変数関数を学習するためのプログラムを以下に示します。先の学習ステップ（２）から（８）に対応します。
//////////////////////////////////
//ニューラルネットワークの生成
//////////////////////////////////
var nn = new NN( W, B, h, sigma, eta );
var data1 = [];//グラフ描画用データ
//学習回数
for( var t=0; t<T; t++){
//ミニバッチ
for( var xi = 0; xi<=M; xi++ ){
//入力値
var x = x_min + (x_max - x_min) * Math.random();
var X0 = [ x ];
//入力層へのインプット
nn.setInput( X0 );
//出力層へのアウトプット
var X2 = nn.getOutput();
var y = X2[0];
//損失関数値の計算
var _L = 1.0/2.0*( y-f( x ) )*( y-f( x ) );
//重みの勾配の計算
for( var i = 0; i < nn.W.length; i++ ){
for( var j = 0; j < nn.W[ i ].length; j++ ){
for( var k = 0; k < nn.W[ i ][ j ].length; k++ ){
nn.W[ i ][ j ][ k ] += d;
nn.setInput( X0 );
var X2 = nn.getOutput();
var y = X2[ 0 ];
var L = 1.0/2.0 * ( y - f( x ) ) * ( y - f( x ) );
nn.W[ i ][ j ][ k ] -= d;//もとに戻しておく
nn.dLdW[ i ][ j ][ k ] += ( L - _L ) / d /M;
}
}
}
//バイアスの勾配の計算
for( var i = 0; i < nn.B.length; i++ ){
for( var j = 0; j < nn.B[ i ].length; j++ ){
nn.B[ i ][ j ] += d;
nn.setInput( X0 );
var X2 = nn.getOutput();
var y = X2[ 0 ];
var L = 1.0/2.0*( y - f( x ) )*( y - f( x ) );
nn.B[ i ][ j ] -= d;
nn.dLdB[ i ][ j ] += ( L - _L ) / d /M;
}
}
}
//重みとバイアスを更新
nn.updateW();
nn.updateB();
//チェック
var sumL = 0;
for( var xi = 0; xi<=M; xi++ ){
//入力値
var x = x_min + (x_max - x_min) * xi/M;
var X0 = [ x ];
nn.setInput( X0 );
var X2 = nn.getOutput( );
var y = X2[0];
sumL += 1.0/2.0*( y-f( x ) )*( y-f( x ) );
}
data1.push([ t, sumL ]);
nn.resetDLdW();
nn.resetDLdB();
}
