HOME > natural science Laboratory > コンピュータ・シミュレーション講座 > ゼロから作るDeep Learning

ゼロから作るDeep Learning
1n1型２層ニューラルネットワークで１変数関数を学習させてみる１：勾配法による学習計算アルゴリズム

文責：遠藤 理平 （2017年4月13日） カテゴリ：ゼロから作るDeep Learning(49)

昨今注目を集めているAI（人工知能）を学びたいと思い立ち、ディープラーニング（Deep Learning、深層学習）と呼ばれるAIの数理モデルである多層構造のニューラルネットワークを書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」を参考にを独習していきたいと思います。本書籍ではプログラミング言語としてPythonが利用されていますが、本項ではJavaScriptで実装していきます。

目次


１変数関数の学習

本項では「1n1型２層ニューラルネットワークの実装（学習なし）」にて示した、あらかじめ与えられている重みとバイアスに対する1n1型ニューラルネットワークを改良して、簡単な例として１変数関数を学習させる計算アルゴリズムを示します。 入力xに対してy=f(x)で計算したy値を教師信号として学習（重みとバイアスの最適化）させて、元の関数と同等の性質をもつニューラルネットワークを構成します。

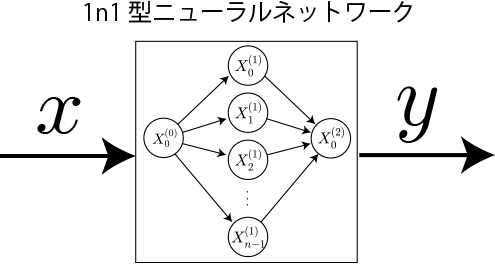
20170413-1.png

（※）１変数関数は入力１つ（x）に対して出力１つ（y）なので、1n1型ニューラルネットワークで構成可能となります。

損失関数の定義

入力に対する出力が正解とどの程度外れているかを表す指標として書籍「ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装」のp.88で紹介されている損失関数を定義します。今回出力は１個なので、入力xに対してニューラルネットワークの出力をy、正しい値を\bar{y}とした場合の損失関数を

L=\frac{1}{2}(y-\bar{y})^2

と定義します。この関数はもし正解と一致した場合に最小値０、正解から外れるほど大きな値になります。1n1型ニューラルネットワーク（前項）の場合、この損失関数は重みとバイアスと入力値の関数

L( W^{(0)}_0,W^{(0)}_1,\cdots,W^{(0)}_{n-1};W^{(1)}_0,W^{(1)}_1\cdots,W^{(0)}_{n-1};b^{(0)}_0,b^{(0)}_1\cdots b^{(0)}_{n-1},b_0^{1)};x )

となり、この関数が小さくなるように重みとバイアスを調整すれば良いことになります。

重みとバイアスの調整方法

「準備３：多変数関数の数値微分と極小値の探索」に従って、重みとバイアスの多変数関数である損失関数を勾配を計算して、勾配の下向き重みとバイアスを調整します。具体的な計算式は次のとおりです。

W_i^{(n)} = W_i^{(n)}-\eta\, \frac{\partial L}{\partial W_i^{(n)}}
b_i^{(n)} = b_i^{(n)}-\eta\, \frac{\partial L}{\partial b_i^{(n)}}

JavaScriptによる実装

NNクラスの拡張

前項までで開発したニューラルネットワークを表すNNクラスをさらに拡張します。 具体的には、重みとバイアスの勾配を格納するプロパティ（多重配列）と勾配から上記のアルゴリズムで値を更新するメソッドをそれぞれ用意します。 


//ニューラルネットワーク
var NN = function( W, B, h, sigma ){
	//重み
	this.W = W;
	//W.length : 層数
	//W[].length : 列（後ニューロン数）
	//W[][].length : 行（前ニューロン数）
	//バイアス
	this.B = B;

	//偏微分値を格納する多重配列
	this.dLdW = [];
	this.dLdB = [];

	//活性化関数
	this.h = h;
	this.sigma = sigma;

	//ニューロンの初期化
	this.X = [];

	//学習率
	this.eta = 0.1;

	this.setup();

}

NN.prototype.setup = function(  ){

	////////////////////////////////////////////
	// ニューロンの初期化
	////////////////////////////////////////////
	for( var i = 0; i < W.length; i++ ){

		this.X[ i ] = [];

		for( var j = 0; j < W[ i ][ 0 ].length; j++ ){

			this.X[ i ][ j ] = 0;

		}

	}
	//出力層
	this.X[ W.length ] = [];
	for( var j = 0; j < W[ W.length-1 ].length; j++ ){
		this.X[ W.length ][ j ] = 0;
	}

	////////////////////////////////////////////
	// 重み格納用多重配列と偏微分値格納多重配列の初期化
	////////////////////////////////////////////
	for( var i = 0; i < this.W.length; i++ ){

		this.dLdW[ i ] = [];

		for( var j = 0; j < this.W[ i ].length; j++ ){

			this.dLdW[ i ][ j ] = [];

			for( var k = 0; k < this.W[ i ][ j ].length; k++ ){

				this.dLdW[ i ][ j ][ k ] = 0;

			}
		}
	}

	////////////////////////////////////////////
	// バイアス格納用多重配列
	////////////////////////////////////////////
	for( var i = 0; i < this.B.length; i++ ){

		this.dLdB[ i ] = [];

		for( var j = 0; j < this.B[ i ].length; j++ ){

			this.dLdB[ i ][ j ] = 0;

		}

	}

}
//重み多重配列の値を更新
NN.prototype.updateW = function(  ){

	for( var i = 0; i < this.W.length; i++ ){
		for( var j = 0; j < this.W[ i ].length; j++ ){
			for( var k = 0; k < this.W[ i ][ j ].length; k++ ){

				this.W[ i ][ j ][ k ] -=  this.eta * this.dLdW[ i ][ j ][ k ] ;

			}
		}
	}
}
//バイアス多重配列の値を更新
NN.prototype.updateB = function(  ){

	for( var i = 0; i < this.B.length; i++ ){
		for( var j = 0; j < this.B[ i ].length; j++ ){

			this.B[ i ][ j ] -=  this.eta * this.dLdB[ i ][ j ];

		}
	}

}
//入力層（０層目ニューロン値）へのインプット
NN.prototype.setInput = function( Input ){

	for( var i = 0; i < Input.length; i++ ){

		this.X[ 0 ][ i ] = Input[ i ];
	}

}
//出力層へのアウトプット
NN.prototype.getOutput = function(){

	//各層ニューロン値の計算
	for( var i = 0; i < W.length; i++ ){

		this.multiplayMatrixVector ( this.W[ i ], this.X[ i ], this.X[ i+1 ] );
		this.addVectors ( this.X[ i+1 ], this.B[ i ], this.X[ i+1 ] );

		//活性化関数の実行
		if( i<W.length-1 ){
			//隠れ層
			this.adoptAFh( this.X[ i+1 ], this.X[ i+1 ] );
		} else {
			//出力層
			this.adoptAFsigma( this.X[ i+1 ], this.X[ i+1 ] );
		}
	}

	return this.X[ this.X.length -1 ];
}

//行列×ベクトルの計算
NN.prototype.multiplayMatrixVector = function( M, V, C ){
	C = C || [];

	var Mgyou = M.length;
	var Mretu = M[ 0 ].length;

	for( var i = 0; i < Mgyou; i++ ){

		C[ i ] =0;

		for( var j = 0; j < Mretu; j++ ){

			C[ i ] += M[ i ][ j ] * V[ j ];

		}

	}

	return C;
}
//ベクトルの和
NN.prototype.addVectors = function( V1, V2, V3 ){
	V3 = V3 || [];

	for( var i = 0; i < V1.length; i++ ){

		V3[ i ] = V1[ i ] + V2[ i ];

	}

	return V3;
}
//活性化関数の実行
NN.prototype.adoptAFh = function( V_in, V_out ){
	V_out = V_out || [];

	for( var i = 0; i < V_in.length; i++ ){

		V_out[ i ] = this.h( V_in[ i ] );

	}

	return V_out;
}
//活性化関数の実行
NN.prototype.adoptAFsigma = function( V_in, V_out ){
	V_out = V_out || [];

	for( var i = 0; i < V_in.length; i++ ){

		V_out[ i ] = this.sigma( V_in[ i ] );

	}

	return V_out;
}

学習のテスト

NNクラスにはまだ学習の機能はありません。最も単純な１変数関数f(x)=xに対して、 １回だけ学習させて損失関数の値が減少することを確認します。１層目のニューロン数を１０個として、重みやバイアスの初期値はすべて-0.5から0.5のランダムな値を与え、学習率0.1として計算しています。
なお、計算結果は以下のような形式でコンソール（「F12」で表示）に出力します。

入力x= 0.33935287279430937
学習前y= 0.035895558696165
学習後y= 0.08625886525202564
損失関数の変化 -0.014014882412923133

入力値は0から1までのランダムな値を与えているため実行ごとに結果が異なります。ほとんどの場合で損失関数はマイナスになることが確認できます。 たまに損失関数がプラスになる理由は、重みとバイアスの勾配を別々に変化させれば損失関数を必ず減少する方向に変化させているわけですが、重みとバイアスの勾配をすべて変化させた際に、たまたま結果として増加してしまう方向に向かってしまったことを意味します。十分な回数の学習を行うことで、この増加分は結果的に無視されます。
次項では様々な条件における学習効果について検証します。 

//第1層のニューロン数
var N1 = 10;
//関数の範囲
var x_min = 0;
var x_max = 1;
//関数
function f( x ){
	return x;
}

//////////////////////////////////
//ニューラルネットワークの生成
var nn = new NN( W, B, h, sigma );
var d = 0.01;

//////////////////////////////////
// 第１回目の学習

//入力値
var x = x_min + (x_max - x_min) * Math.random();
var X0 = [ x ];
console.log( "入力", x );


//入力層へのインプット
nn.setInput( X0 );
//出力層へのアウトプット
var X2 = nn.getOutput();
var y = X2[0];
console.log( "出力１回目", y );

//学習前
var L0 = 1.0/2.0*( y-f( x ) )*( y-f( x ) );

for( var i = 0; i < nn.W.length; i++ ){
	for( var j = 0; j < nn.W[ i ].length; j++ ){
		for( var k = 0; k < nn.W[ i ][ j ].length; k++ ){

			nn.W[ i ][ j ][ k ] += d;
			nn.setInput( X0 );

			var X2 = nn.getOutput();
			var y = X2[ 0 ];
			var L1 = 1.0/2.0*( y - f( x ) )*( y - f( x ) );

			nn.W[ i ][ j ][ k ] -= d;//もとに戻しておく
			nn.dLdW[ i ][ j ][ k ] = ( L1 - L0 ) / d;

		}
	}
}

nn.updateW();


for( var i = 0; i < nn.B.length; i++ ){
	for( var j = 0; j < nn.B[ i ].length; j++ ){

		nn.B[ i ][ j ] += d;
		nn.setInput( X0 );
		var X2 = nn.getOutput();
		var y = X2[ 0 ];
		var L1 = 1.0/2.0*( y - f( x ) )*( y - f( x ) );
		nn.B[ i ][ j ] -= d;
		nn.dLdB[ i ][ j ] = ( L1 - L0 ) / d;

	}
}
nn.updateB();

//チェック
nn.setInput( X0 );
var X2 = nn.getOutput(  );
var y = X2[0];
var L1 = 1.0/2.0*( y-f( x ) )*( y-f( x ) );
console.log( "出力２回目", y );
console.log( "損失関数の変化", L1 - L0 );


▲このページのトップ ｜ NPO法人 natural science トップ

関連記事

ゼロから作るDeep Learning

【ニューラルネットワークの基礎研究31】ニューラルネットワークによる関数近似の検証（中間層１層の場合） 2018.08.02 【遠藤 理平｜ゼロから作るDeep Learning】

【ルンゲ・クッタで行こう！】水平自由単振子運動シミュレーション 2018.05.30 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】


【ニューラルネットワークの基礎研究30】任意の初期条件に対する運動を学習（重力＋空気抵抗力） 2018.05.26 【遠藤 理平｜ゼロから作るDeep Learning】

【ルンゲ・クッタで行こう！】単振子強制振動運動シミュレーション 2018.05.25 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】


【ニューラルネットワークの基礎研究29】放物運動の初期位置と初速度と経過時間から位置と速度を学習 2018.05.23 【遠藤 理平｜ゼロから作るDeep Learning】

【ニューラルネットワークの基礎研究28】放物運動の現在の位置と速度から未来の位置と速度を学習 2018.05.22 【遠藤 理平｜ゼロから作るDeep Learning】


【ニューラルネットワークの基礎研究27】放物運動の粘性抵抗係数と初速度と投射角度から飛距離を学習してみる 2018.05.10 【遠藤 理平｜ゼロから作るDeep Learning】

【ニューラルネットワークの基礎研究26】放物運動の軌跡から粘性抵抗係数と慣性抵抗係数を見積もる 2018.05.08 【遠藤 理平｜ゼロから作るDeep Learning】


【ニューラルネットワークの基礎研究25】放物運動の軌跡から空気抵抗係数を学習してみる 2018.05.07 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】

【ニューラルネットワークの基礎研究24】LASSO回帰因子を損失値に応じて小さくしてみる 2018.05.05 【遠藤 理平｜ゼロから作るDeep Learning】



▲このページのトップ ｜ NPO法人 natural science トップ