高速フーリエ変換の動作チェック（C++）

以前、JavaScriptで作成した高速フーリエ変換用関数をC言語に書き直しました。 シュレディンガー方程式を数値的に解くためにこれを用いる予定です。

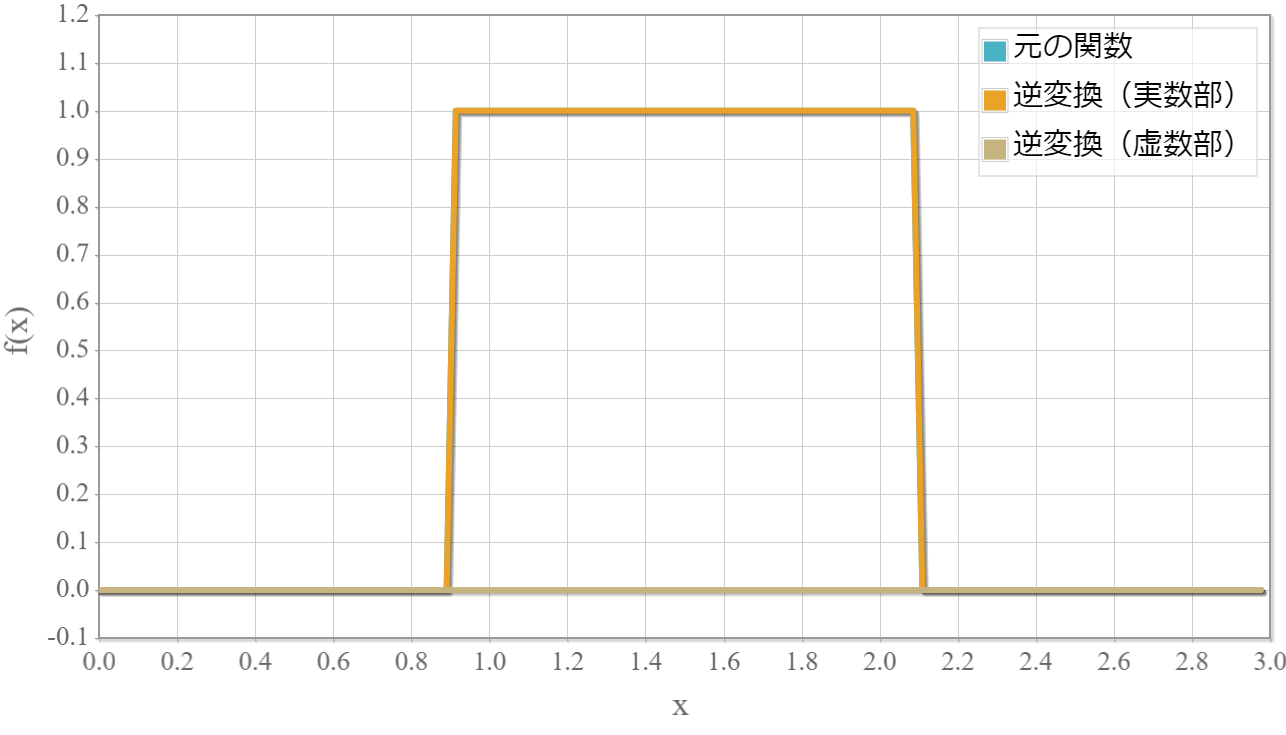
元の関数と逆変換の結果

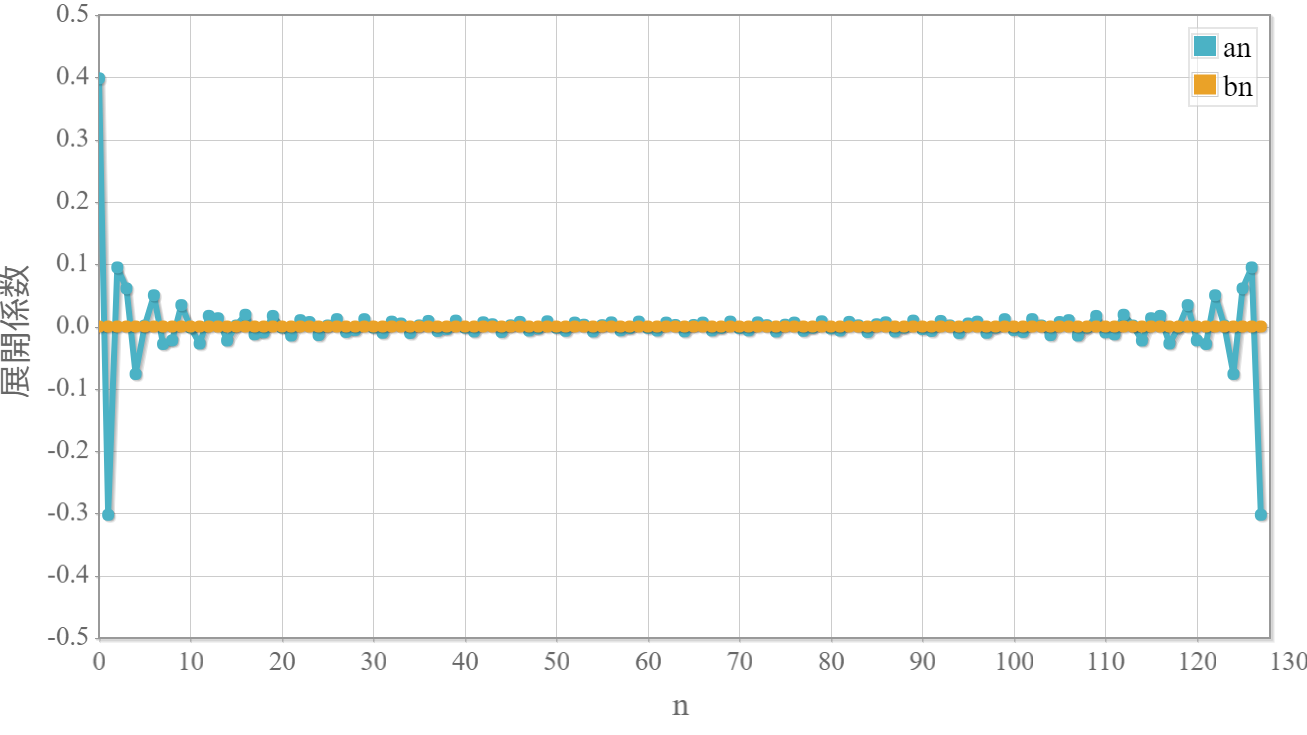
展開係数

プログラムソース

////////////////////////////////////////////////////////////////////
// 高速フーリエ変換
////////////////////////////////////////////////////////////////////
#define _USE_MATH_DEFINES
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <iostream>
#include <fstream>
#include <sstream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>

/////////////////////////////////////////////////////////////////
//項数と空間距離
const int N = 128;
double L = 3.0;

//高速フーリエ変換
void FFT(double* an, double* bn, int N, bool Inverse) {
	/////////////////////////////////////////
	//参考：Javaで学ぶシミュレーションの基礎
	/////////////////////////////////////////
	// 入力
	// N  ： 項数（2のべき乗）
	// an : 実数配列（順変換：実数空間データを項数Nで指定、逆変換：展開係数a(n)）
	// bn : 実数配列（順変換：虚数空間データを項数Nで指定、逆変換：展開係数b(n)）
	// Inverse : 逆変換の場合に true
	/////////////////////////////////////////
	// 出力
	// an : 実数配列（順変換：展開係数a(n)、逆変換：実数空間データ）
	// bn : 実数配列（順変換：展開係数b(n)、逆変換：虚数空間データ）
	/////////////////////////////////////////

	int ff = Inverse ? 1 : -1;

	int* rot = new int[N];

	for (int i = 0; i < N; i++) rot[i] = 0;

	int nhalf = N / 2, num = N / 2;
	double sc = 2.0 * M_PI / N;

	while (num >= 1) {

		for (int j = 0; j < N; j += 2 * num) {

			int phi = rot[j] / 2;
			int phi0 = phi + nhalf;
			double c = cos(sc * phi);
			double s = sin(sc * phi * ff);

			for (int k = j; k < j + num; k++) {

				int k1 = k + num;
				double a0 = an[k1] * c - bn[k1] * s;
				double b0 = an[k1] * s + bn[k1] * c;
				an[k1] = an[k] - a0;
				bn[k1] = bn[k] - b0;
				an[k] = an[k] + a0;
				bn[k] = bn[k] + b0;
				rot[k] = phi;
				rot[k1] = phi0;
			}
		}
		num = num / 2;
	}

	for (int i = 0; i < N; i++) {
		int j = rot[i];
		if (j > i) {

			double tmp = an[i];
			an[i] = an[j];
			an[j] = tmp;

			tmp = bn[i];
			bn[i] = bn[j];
			bn[j] = tmp;

		}
	}

	if (!Inverse) {
		for (int i = 0; i < N; i++) {
			an[i] = an[i] / N;
			bn[i] = bn[i] / N;

		}
	}

	delete[] rot;
}

//元の関数
double f( double x) {
	//	return Math.sin( 2 * Math.PI / L * 2 * x );
	if (L / 2 - L / 5 < x  &&  x < L / 2 + L / 5) return 1;
	else return 0;
}


/////////////////////////////////////////////////////////////////
std::string folder = "output";//作成するフォルダ名
std::string filename1 = "FFT.txt";//ファイル名
std::string filename2 = "FFT_.txt";//ファイル名
const int precision_N = 4;

int main() {

	//フォルダ生成
	_mkdir(folder.c_str());
	std::string filepath1 = folder + "/" + filename1;
	std::string filepath2 = folder + "/" + filename2;

	//展開係数
	double an[N], bn[N];

	for (int i = 0; i<N; i++) {
		double x = L / N * i;
		an[i] = f(x);
		bn[i] = 0;
	}

	//順変換の実行
	FFT(an, bn, N, false);

	//出力ストリームによるファイルオープン
	std::ofstream fout1;
	fout1.open(filepath1.c_str());
	fout1 << "#x:n" << std::endl;
	fout1 << "#y:展開係数" << std::endl;
	fout1 << "#legend: an bn" << std::endl;
	fout1 << "#showLines: true true true true" << std::endl;
	fout1 << "#showMarkers: true true false false" << std::endl;
	fout1 << "#fills: false false false false" << std::endl;
	fout1 << "#xrange:0 128 10" << std::endl;
	fout1 << "#yrange:-0.5 0.5 0.1 " << std::endl;
	for (int i = 0; i < N; i++) {
		fout1 << i << " " << an[i] << " " << bn[i] << std::endl;
	}
	fout1.close();


	//逆変換用
	double _an[N], _bn[N];

	for (int n = 0; n < N; n++) {
		_an[n] = an[n];
		_bn[n] = bn[n];
	}

	//逆変換の実行
	FFT(_an, _bn, N, true);

	//出力ストリームによるファイルオープン
	std::ofstream fout2;
	fout2.open(filepath2.c_str());
	fout2 << "#x:x" << std::endl;
	fout2 << "#y:f(x)" << std::endl;
	fout2 << "#legend: 元の関数 逆変換（実数部） 逆変換（虚数部）" << std::endl;
	fout2 << "#showLines: true true true true" << std::endl;
	fout2 << "#showMarkers: false false false false" << std::endl;
	fout2 << "#fills: false false false false" << std::endl;
	fout2 << "#xrange:0 3 0.2" << std::endl;
	fout2 << "#yrange:-0.1 1.1 0.1 " << std::endl;
	for (int i = 0; i < N; i++) {
		double x = L / N * i;
		fout2 << x << " " << f(x) << " " << _an[i] << " " << _bn[i] << std::endl;
	}
	fout2.close();

}

・http://www.natural-science.or.jp/files/physics/FFT_test.cpp
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。