ルジャンドル陪関数の漸化式と規格化

ルジャンドル陪関数は、

(1)

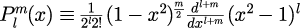
で定義される関数で、を次数（degree）、を位数（order）と呼ばれる２つの指数で指定されます。 ただし、と、には

(2)

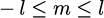
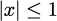
の制限があります。 式(1)で与えられるルジャンドル陪関数は解析的には便利な場合が多いですが、 数値的に扱う際には非常に不便なので、エルミート多項式の場合と同様に漸化式を利用します。

ルジャンドル陪関数の漸化式

位数に対して、

(3)

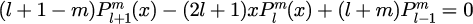
が成り立ちます。ただし、次数は以上である必要があります。 数値的には、

(4)

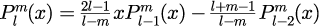
と変形したほうが都合が良いです。つまり、連続する２つの次数に対する依存性が得られれば、 次の次数の依存性を数値的に得ることができます。 漸化式の初期値として、とにおけるを

(5)

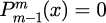
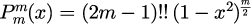
と与えることで、位数かつのルジャンドル陪関数を計算することができます。 の場合には、

(6)

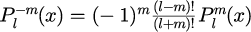
の関係式を用います。これで任意のとを満たす任意のに対するルジャンドル陪関数を計算することができことになります。

ルジャンドル陪関数の直交性と規格化

異なる次数のルジャンドル陪関数の内積は

(7)

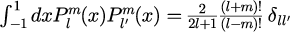
となります。つまり、

(8)

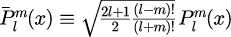
と新しく定義することでルジャンドル陪関数を規格化することができます。 規格化ルジャンドル陪関数の漸化式は式(4)から

(9)

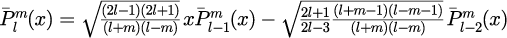
となり、初期値は

(10)

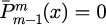
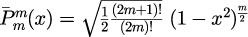
となります。また、の関係式(6)は

(11)

と変形することができます。以上で得られる規格化ルジャンドル陪関数は

(12)

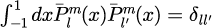
を満たします。

計算結果

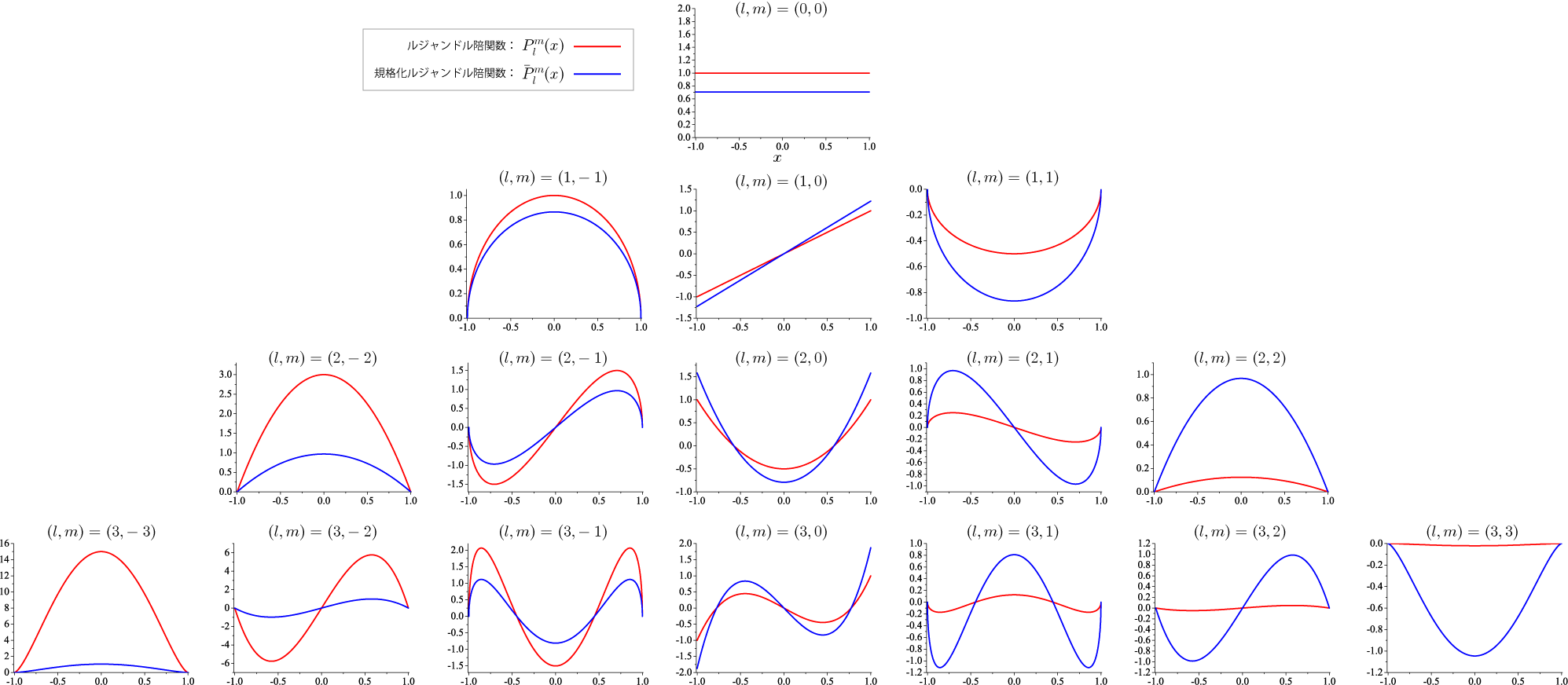
ルジャンドル陪関数の依存性

（）に対して、 との計算結果を示します。

拡大する

規格化ルジャンドル陪関数の直交性の確認

式(9),(10)で得られた規格化ルジャンドル陪関数の直交性を確かめます。 下記は式(12)を計算した結果です（左から順にと式(12)の計算結果）。

0 0 0 1
0 0 1 2.23525e-017
0 0 2 2.48542e-016
0 0 3 3.15303e-017
0 1 0 2.23525e-017
0 1 1 1
0 1 2 2.28706e-016
0 1 3 1.52749e-012
0 2 0 2.48542e-016
0 2 1 2.28706e-016
0 2 2 1
0 2 3 9.9772e-017
0 3 0 3.15303e-017
0 3 1 1.52749e-012
0 3 2 9.9772e-017
0 3 3 1
1 1 1 1
1 1 2 6.55298e-017
1 1 3 -9.34794e-013
1 2 1 6.55298e-017
1 2 2 1
1 2 3 -6.85308e-017
1 3 1 -9.34794e-013
1 3 2 -6.85308e-017
1 3 3 1
2 2 2 1
2 2 3 1.58455e-017
2 3 2 1.58455e-017
2 3 3 1
3 3 3 1

が実現できていることが確認できます。

C言語プログラムソース

数値積分にはシンプソン法（シンプソン法を利用して積分を数値計算する） を用いています。

/*漸化式を用いてルジャンドル陪関数と規格化ルジャンドル陪関数を描画するプログラム
＋直交性の確認
(2011.12.27 公開)*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
double Factorial1(int n);
double Factorial2(int n);
const int l_max = 3;
const int kizami = 2000;
double Legendre( int m, int l, double x);           //ルジャンドル陪関数
double NormalizedLegendre( int m, int l, double x); //規格化ルジャンドル陪関数
string folder = "Legendre";//作成するフォルダ名
double Simpson(double a, double b, int m, int l1,  int l2);//シンプソン法
double f(double x, int m, int l1,  int l2){
  return NormalizedLegendre( m, l1 , x) * NormalizedLegendre(m, l2, x);
}

int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(8);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif
  double x_min = -1.0;
  double x_max =  1.0;

  for(int l=0; l<=l_max; l++)
  {
    for(int m=-l; m<=l; m++)
    {
      char str[200];
      string str1;
      ofstream fout_s;
      sprintf(str, "/Legendre%d_%d.data", l, m); str1 = folder + str;
      fout_s.open(str1.c_str());
      for(int i=0; i<=kizami; i++)
      {
        double x = x_min + (x_max-x_min)/double(kizami)*double(i);
        fout_s << x << " " << Legendre(m,l, x) << " " << NormalizedLegendre(m,l, x) << endl;
      }
      fout_s.close();
    }
  }

  ofstream ofs( "Legendre_bisect.data" );
  for(int m=0; m<=l_max; m++)
  {
    for(int l1=m; l1<=l_max; l1++)
    {
      for(int l2=m; l2<=l_max; l2++)
      {
        ofs << m << " " << l1 <<" " << l2 << " " <<  Simpson( x_min, x_max, m, l1, l2) << endl;
      }
    }
  }
  ofs.close();
}
double Legendre( int m, int l, double x)
{
  int mm = abs(m);
  if( mm>l )  return 0;
  double r0, r1, r2;
    r0 = 0.0;
    r1 = pow(1.0-x*x, double(mm)/2.0) * Factorial2(2*mm-1);
    if( mm==l && m>=0) return r1;
    if( mm==l && m<0)  return r1 * pow(-1.0,mm) * Factorial1(l-mm)/Factorial1(l+mm) ;
    for(int ll = mm+1; ll<=l; ll++ ){
      r2 = ((2.0*ll-1.0)*x*r1 - (ll+mm-1.0)*r0)/(ll-mm);
      r0 = r1;
      r1 = r2;
    }
  if(m>=0) return r2;
  else return r2 * pow(-1.0,mm) * Factorial1(l-mm)/Factorial1(l+mm) ;
}
double NormalizedLegendre( int m, int l, double x)
{
  int mm = abs(m);
  if( mm>l )  return 0;
  double r0, r1, r2;
    r0 = 0.0;
    r1 = pow(1.0-x*x, double(mm)/2.0) * sqrt( 1.0/2.0 * Factorial2(2*mm+1)/Factorial2(2*mm));
    if( mm==l && m>=0) return r1;
    if( mm==l && m<0)  return r1 * pow(-1.0,mm);
    for(int ll = mm+1; ll<=l; ll++ ){
      r2 = sqrt((2.0*ll-1.0)*(2.0*ll+1.0)/((ll+mm)*(ll-mm))) *x*r1 - sqrt((ll+mm-1.0)*(ll-mm-1.0)/((ll+mm)*(ll-mm)) * (2.0*ll+1.0)/(2.0*ll-3.0) ) *r0;
      r0 = r1;
      r1 = r2;
    }
  if(m>=0) return r2;
  else return r2 * pow(-1.0,mm) ;
}

double Factorial1(int n)
{
  if( n<=0 ) return 1.0;
  double F = 1.0;
  for(int i=n; i>=2; i--){
    F *= double(i);    
  }
  return F;
}
double Factorial2(int n)
{
  if( n<=0 ) return 1.0;
  double F = 1.0;
  for(int i=n; i>=2; i=i-2){
    F *= double(i);    
  }
  return F;
}
double Simpson(double a, double b, int m, int l1, int l2)
{
  double ss1 =0.0;
  for(int i=1; i<=kizami/2-1; i++){
    double x = a + (b-a)/double(kizami) * double(2*i);
    ss1 += f(x, m, l1, l2);
  }
  double ss2 =0.0;
  for(int i=1; i<=kizami/2; i++){
    double x = a + (b-a)/double(kizami) * double(2*i-1);
    ss2 += f(x, m, l1, l2);
  }
  return  (b-a)/(3.0*double(kizami)) * ( f(a, m, l1, l2) + f(b, m, l1, l2) + 2.0 * ss1 + 4.0 * ss2 );
}

ファイル

C言語ソースファイル

■漸化式を用いてルジャンドル陪関数と規格化ルジャンドル陪関数を描画するプログラム

Illustratorファイル

■ルジャンドル陪関数.ai

Originファイル

■ルジャンドル陪関数.OPJ