エルミート多項式の規格化

エルミート多項式は「エルミート多項式の直交性を確かめる」で示したとおり、内積は

(1)

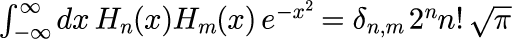
となります。。 改めて、規格化エルミート多項式を

(2)

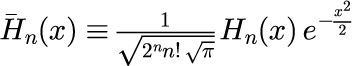
と置くことで式(1)の内積は

(3)

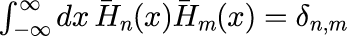
となります。「エルミート多項式の直交性を確かめる」で与えられたエルミート多項式の漸化式は規格化に伴って

(4)

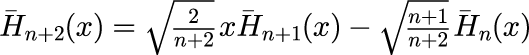
と変形されます。 n=10 におけるエルミート多項式と規格化エルミート多項式を描画したのが次の図です。

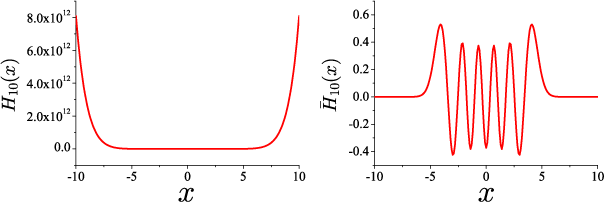
漸化式を用いてエルミート多項式と規格化エルミート多項式を描画するプログラムにて計算

大きな x に対して発散するエルミート多項式に対して、規格化エルミート多項式は 0 に収束していることがわかります。

C言語プログラムソース

数値積分にはシンプソン法（シンプソン法を利用して積分を数値計算する） を用いています。

漸化式を用いてエルミート多項式と規格化エルミート多項式を描画するプログラム

/* 漸化式を用いてエルミート多項式と規格化エルミート多項式を描画するプログラム
(2011.11.05 公開) */

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
double Hermite( int n, double x );  //エルミート多項式
double NormalizedHermite( int n, double x ); //規格化エルミート多項式
string folder = "data";//作成するフォルダ名

int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(11);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif
  double x_min = -10;
  double x_max = 10;

  for(int n=0; n<=20; n++){
    char str[200];
    string str1;
    ofstream fout_s;
    sprintf(str, "/Hermite%d.data", n); str1 = folder + str;
    fout_s.open(str1.c_str());
    for(double x = x_min; x<= x_max ; x+=0.1){
      fout_s << x << " " << Hermite(n, x) << " " << NormalizedHermite(n, x) << endl;
    }
    fout_s.close();
  }
}
double Hermite( int n, double x )
{
  double y0, y1, y2;
  y0 = 1.0;
  if( n==0 ) return y0;
  y1 = 2.0 * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = 2.0 * x * y1 - 2.0 * (m-1) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}
double NormalizedHermite( int n, double x )
{
  double y0, y1, y2;
  y0 = sqrt(1.0/sqrt(PI)) * exp(-pow(x,2)/2);
  if( n==0 ) return y0;
  y1 = sqrt(2.0/sqrt(PI)) * exp(-pow(x,2)/2) * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = sqrt(2.0/double(m)) * x * y1 - sqrt(double(m-1)/double(m)) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}

規格化エルミート多項式の直交性を確かめるプログラム

/* 規格化エルミート多項式の直交性を確かめるプログラム
(2011.11.05 公開) */

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);

int kizami = 100000;
double L = 50;

double Hermite( int n, double x );  //エルミート多項式
double NormalizedHermite( int n, double x ); //規格化エルミート多項式
double Simpson(double a, double b, int n, int m);

double f(double x, int n, int m){
  return NormalizedHermite(n, x) * NormalizedHermite(m, x);
}
string folder = "data";//作成するフォルダ名

int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(4);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif

  ofstream ofs( "Hermite_bisect.data" );
  for(int n=10; n<=10; n++){
    for(int m=0; m<=20; m++){
      ofs << n <<" " << m << " " <<  Simpson( -L, L , n, m) << endl;
    }
    ofs << " " << endl;
  }
}
double NormalizedHermite( int n, double x )
{
  double y0, y1, y2;
  y0 = sqrt(1.0/sqrt(PI)) * exp(-pow(x,2)/2);
  if( n==0 ) return y0;
  y1 = sqrt(2.0/sqrt(PI)) * exp(-pow(x,2)/2) * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = sqrt(2.0/double(m)) * x * y1 - sqrt(double(m-1)/double(m)) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}
double Simpson(double a, double b, int n, int m)
{
  double ss1 =0.0;
  for(int i=1; i<=kizami/2-1; i++){
    double x = a + (b-a)/double(kizami) * double(2*i);
    ss1 += f(x, n, m);
  }
  double ss2 =0.0;
  for(int i=1; i<=kizami/2; i++){
    double x = a + (b-a)/double(kizami) * double(2*i-1);
    ss2 += f(x, n, m);
  }
  return  (b-a)/(3.0*double(kizami)) * ( f(a, n, m) + f(b, n, m) + 2.0 * ss1 + 4.0 * ss2 );
}

ファイルたち

VisualC++のプロジェクトファイル

■漸化式を用いてエルミート多項式と規格化エルミート多項式を描画するプログラム

Illustratorファイル

■エルミート多項式.ai