エルミート多項式の直交性を確かめる

エルミート多項式とは微分方程式

(1)

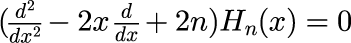
を満たす解で、一般解は微分演算子を用いて

(2)

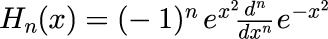
と表すことができます。 エルミート多項式は量子力学のシュレディンガー方程式における調和振動子の一般解を表すのによく利用されます。 具体的表式は

(3)

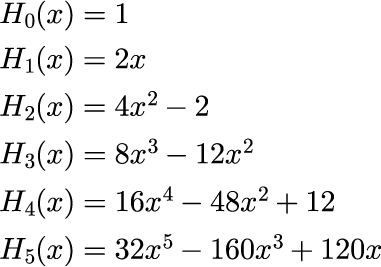
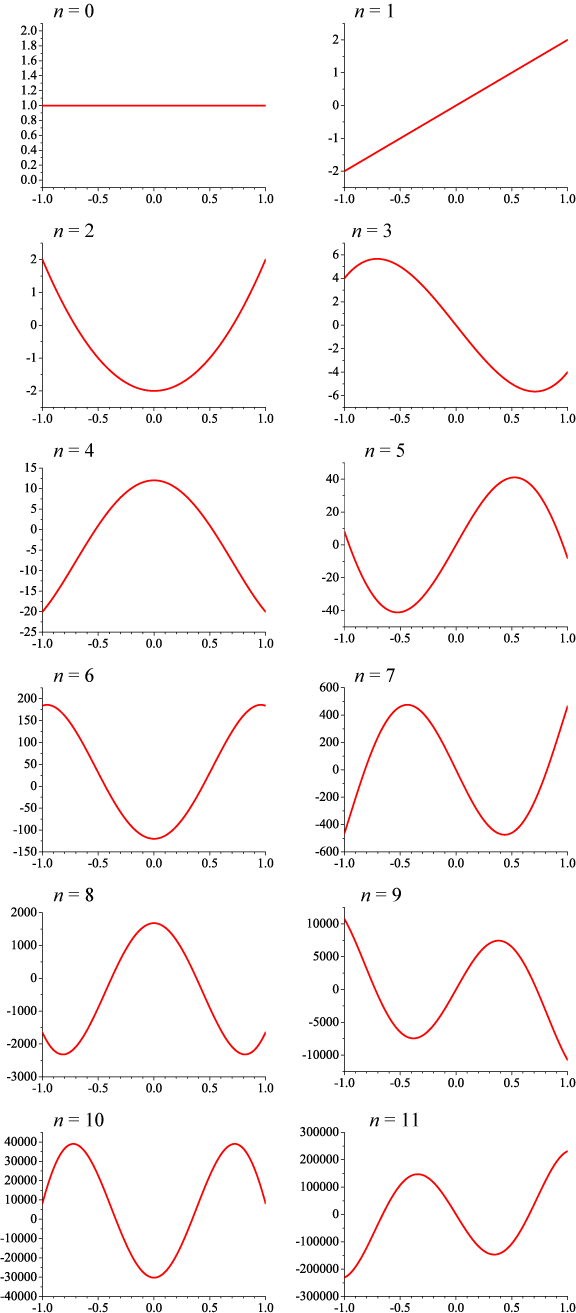
となります。 nが偶数の時は偶関数、nが奇数の場合は奇関数となることがわかります。 n = 0～11 までを描画したのが次の図です。

漸化式を用いてエルミート多項式を描画するプログラムにて計算

上の図は式(2)の関数型を用いて描画したのではなく 数値計算を行う場合、式(2)のような微分形式は取り扱いにくく、式(2)から導かれる漸化式

(4)

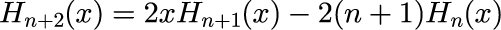
を用いるほうが便利です。上の図も式(4)を用いて描画しました。 また、エルミート多項式は、重み関数 exp(-x^2)を用いて、異なる指数 n による内積が直交していることが知られています。 具体的には

(5)

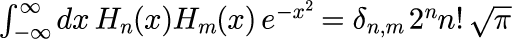
となります。これは任意の関数をエルミート多項式を用いて展開する際に非常に重要となります。 この直交性を数値計算で確かめるわけですが、式(5)の積分範囲は[-∞:∞]であるため、数値的には積分範囲を打ち切る必要があります。 そこで、

(6)

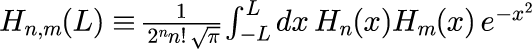
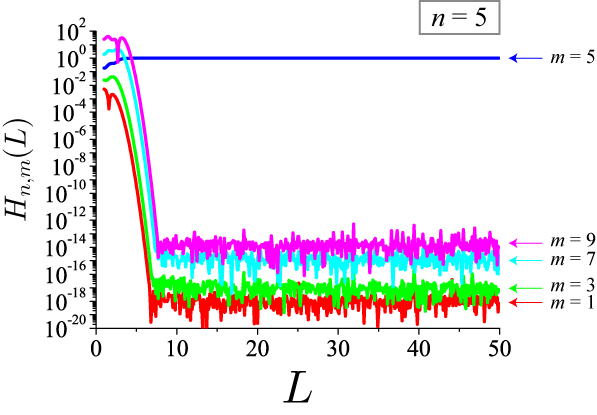
を定義します。L は積分範囲を表すパラメータです。 式(6)のうち、n=5, m=1,3,5,7,9 をプロットしたのが次の図です。

エルミート多項式の直交性と積分範囲の関係にて計算

m = 5 の時に H_{n,m}(L) =1 に収束し、それ以外では ≒ 0 となっていることが確認できます。 積分範囲はおよそ L = 10 程度あれば、収束していることがわかります。

C言語プログラムソース

数値積分にはシンプソン法（シンプソン法を利用して積分を数値計算する） を用いています。

漸化式を用いてエルミート多項式を描画するプログラム

/*
エルミート多項式
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
using namespace std;

double hermite( int n, double x );
int main(){
  int kizami = 10000;
  double x_min = 0;
  double x_max = 1;

  for(int n=0; n<=11; n++){
    char str[200];
    ofstream fout_s;
    sprintf(str, "Hermite%d.data", n);
    fout_s.open(str);

    for(int m=-kizami; m<=kizami; m++){
      double x = x_min + (x_max - x_min) * double(m)/double(kizami);
      fout_s << x << " " << hermite(n, x) << endl;
    }
    fout_s.close();
  }
}
double hermite( int n, double x )
{
  double y0, y1, y2;
  y0 = 1.0;
  if( n==0 ) return y0;
  y1 = 2.0 * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = 2.0 * x * y1 - 2.0 * (m-1) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}

エルミート多項式の直交性と積分範囲の関係

/*
エルミート多項式の直交性と積分範囲の関係を確かめるプログラム
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#if defined(_OPENMP)
  #include <omp.h>
#endif
#if defined(_MSC_VER)
  #include <direct.h>   // Windowsフォルダ作成用
#elif defined(__GNUC__)
  #include <sys/stat.h> //  UNIX系ディレクトリ作成用
#endif
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);

int kizami = 10000;
double L = 50;

double Hermite( int n, double x );
double Simpson(double a, double b, int n, int m);
int Factorial(int n);
int pow(int n, int m);

double f(double x, int n, int m){
  return exp(-pow(x,2)) * Hermite(n, x) * Hermite(m, x);
}

string folder = "data";//作成するフォルダ名

int main(){
  #if defined(_MSC_VER)
    _mkdir(folder.c_str());   // Windowsフォルダ作成
  #elif defined(__GNUC__)
    mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
  #endif
  #if defined(_OPENMP)
    omp_set_num_threads(8);
    cout << "OpenMPを利用します（最大スレッド数："<< omp_get_max_threads() << "）" <<  endl;
  #endif
  #pragma omp parallel
  {
    #pragma omp for //schedule(dynamic, 100)
    for(int n=0; n<=10; n++){
      for(int m=0; m<=10; m++){
        cout << n << " " << m << endl;
        char str[200];
        string str1;
        ofstream fout_s;
        sprintf(str, "/Hermite_bisect_%d-%d.data", n, m); str1 = folder + str;
        fout_s.open(str1.c_str());
        for(double l=1.0; l<=L; l+=0.1){
          fout_s << l << " " << abs( 1.0/double(pow(2,n)) * Simpson( -l, l , n, m)/(Factorial(n)*sqrt(PI))) << endl;
        }
        fout_s.close();
      }
    }
  }
}
double Hermite( int n, double x )
{
  double y0, y1, y2;
  y0 = 1.0;
  if( n==0 ) return y0;
  y1 = 2.0 * x;
  if( n==1 ) return y1;
  for(int m = 2; m<=n; m++ ){
    y2 = 2.0 * x * y1 - 2.0 * (m-1) * y0;
    y0 = y1;
    y1 = y2;
  }
  return y2;
}
double Simpson(double a, double b, int n, int m)
{
  double ss1 =0.0;
  for(int i=1; i<=kizami/2-1; i++){
    double x = a + (b-a)/double(kizami) * double(2*i);
    ss1 += f(x, n, m);
  }
  double ss2 =0.0;
  for(int i=1; i<=kizami/2; i++){
    double x = a + (b-a)/double(kizami) * double(2*i-1);
    ss2 += f(x, n, m);
  }
  return  (b-a)/(3.0*double(kizami)) * ( f(a, n, m) + f(b, n, m) + 2.0 * ss1 + 4.0 * ss2 );
}
int Factorial(int n)
{
  if (n == 0 || n == 1) return 1; 
  return n * Factorial(n-1);
}
int pow(int n, int m)
{
  int k=1;
  if(m==0) return 1;
  for(int i=1; i<=m; i++){
    k *= n;
  }
  return k;
}

以上を用いて具体的には後で、エルミート多項式を用いて展開することができる物理量に対する時間発展を計算します。

ファイルたち

VisualC++のプロジェクトファイル

■漸化式を用いてエルミート多項式を描画するプログラム
■エルミート多項式の直交性と積分範囲の関係

Illustratorファイル

■エルミート多項式.ai

Originファイル

■エルミート多項式.OPJ

参考ページ

■4.4.1　Hermite 微分方程式に関する計算／量子化学ノート（Notes for Quantum Chemistry）
■エルミート多項式／Wikipedia