LabVIEWで微分をプログラムする
微分のプログラム完成までの流れ
1.まずはじめに、微分が何だったのか、教科書の式を参考にする。しかし、習った気はするものの何をしているのか、いまいち分からない。
2.次に、その式の意味を日本語で表せるように考える。文章にしたり、図にしてみたりと、自分が分かりやすいとおもうように考えてみる。
3.最後に、理解できた。と思ったらLab VIEWでプログラミングする。実行結果として出力されたグラフを見ると、そのプログラムがあっているのかどうかが分かる。間違えている場合、自分の考え方や、プログラムの仕方で何が間違えているのか、実行結果を見て考えることができる。
教科書からの微分の式
微分:関数 y = f(x) において、yの変化量 f(x + Δx) -f(x) のxの変化量に対する割合。つま り、現在の位置xからΔxまで変化するときの、関数 f(x) の平均変化率。これは、下記の式によってもとめられる。
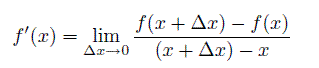
また、関数 f(x) から導関数 f'(x) をもとめることを f(x)を微分するという。
日本語で考えてみる
![]()
上の式はどういう意味なのか。まずはじめに、式の最初に書いてある
まず、分母の(Δx + x) - x というのは、xがどれだけすすんだか。分子の f(Δx + x) - f(x) という
のはyがどれだけすすんだのかを示している。今、xがこれだけ(= Δx) 進んだ時に、yがどれだけ変化するのか、その変化の割合をみている。つまり、これが先ほどみた平均変化率と考えられる。これが図1である。
である。
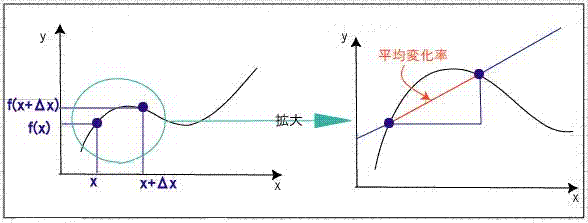
図1.平均変化率
ここで、先ほど省略した
例えば、y = x^2のときは図2のようになる。
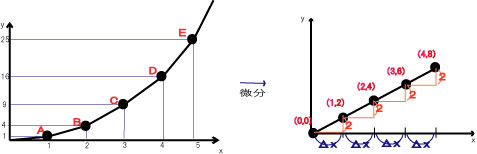
図2.y=x^2とその微分
上図のそれぞれの点の座標は次の通り、 点A(1,1)、点B(2,4)、点C(3,9)、点D(4,16)、点E(5,25)。\par y軸の変化をみたものをそれぞれA'=1, B'=3, C'=5, D'=7, E'=9とおく。 すると、A'B', B'C', C'D', D'E'間の変化量はそれぞれ2となる。
Lab VIEW で微分をプログラム
今回、sin x のグラフを微分するプログラムを作成した。sin x の微分なので、実行結果がcos x になるはず。 まずはじめに、sin x のグラフを作成した。プログラムと実行結果は図3のようになる。プログ ラムの説明は以下の通りである。 ちなみに、プログラムの中で0.1をかけたのは滑らかなグラフにするためである。
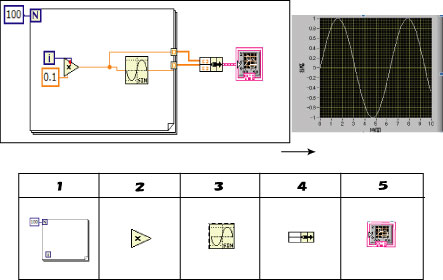
図3.sin xを表示するプログラム
1.四角の中に書かれていることを○回繰り返す。回数をきめるのはNの横の数字(今回は100)。また、「i」というのは、最初の値として0が入っており、一回繰り返すごとに1ずつ加算されていく。
2.左上と左下に入った値をかけた結果が右から出てくる。+、-、/、もそれぞれ、足したもの、引いたもの、割ったものを結果として出す。ちなみに、計算手順は上{足す/引く/かける/割る}下。
3.左から入ってきた値の正弦値を計算する。単位はラジアン。
4.上段につないだものがグラフのx軸に、下段につないだものがグラフのy軸になる。
5.XYグラフとして表示する。
次に、sin x を微分するプログラムを作成した。プログラムと実行結果は図4のようになる。先ほどのsin x のプログラム作成のときと同様に今回も、滑らかなグラフにするために0.1をかけた。
プログラムは式の通りで、f(x + 0.1)という関数からf(x)という関数を引き、それをxの変化分(0.1)で割っている。
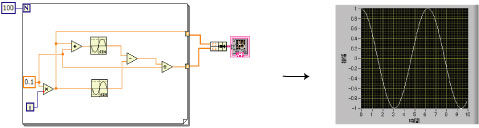
図4.sin xを微分するプログラム
最後に、sinxとそれを微分したプログラムの実行結果をくらべたものが図5である。これを見ると正弦波が余弦波になっていることを確認することができる。
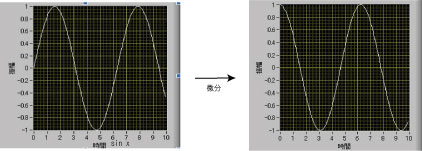
図5.sin x と、sin x を微分した結果のグラフ