HOME > natural science Laboratory > コンピュータ・シミュレーション講座 > TIPS 集

モンテカルロ法を熱平衡状態の計算（メトロポリスの方法）

文責：遠藤 理平 （2009年2月27日） カテゴリ：DirectX(1)｜TIPS 集(107)

モンテカルロ法によるカノニカル集合の熱平衡状態を計算する。 具体的には、粒子間相互作用にレナード・ジョーンズ・ポテンシャル、計算手法ではメトロポリス法を用いて計算する。
（モンテカルロ法の初歩については、モンテカルロ法を試す―円周率の評価―をご覧ください）

レナード・ジョーンズ・ポテンシャル

\sigma は粒子の直径程度。


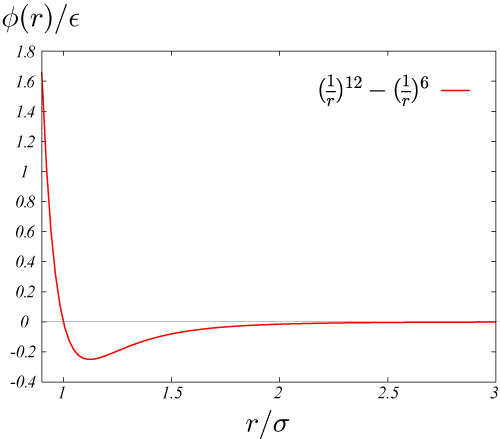
図１：レナード・ジョーンズ・ポテンシャル

計算の手順（メトロポリス法）

ステップ１：Ｎ個の粒子を図のように幅Ｌの立方体に配置する。


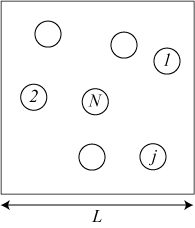
図２：初期配置図

初期配置に対して、各粒子間のレナード・ジョーンズ・ポテンシャルを計算し、Ｎ粒子系のポテンシャルエネルギー(U_0)を計算する。

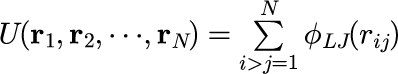
ポテンシャル項

ステップ２

1番目の粒子の位置座標をずらし、Ｎ粒子系のポテンシャルエネルギー(U_1)を計算する（図３左）。


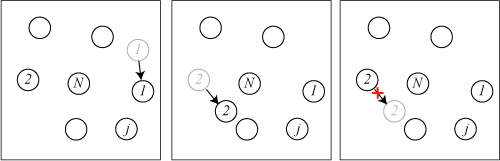
状態kから状態iへの遷移確率をP_{ki}とした場合、メトロポリスの方法では、遷移確率を次の関係式で決定する。

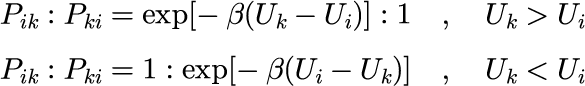
メトロポリスの方法

つまり、 U_1<U_0 ならば、遷移確率１で遷移する（必ず遷移する）。逆に、 U_1>U_0 ならば、遷移確率 $\exp[-\beta(U_1 - U_0)](<1)$ で遷移する。（図３左は遷移した場合の図）
次に、２番目の粒子の位置座標をずらし、Ｎ粒子系のポテンシャルエネルギー（U_2）を計算する（図３中）。先と同様に、ポテンシャルエネルギー U_2, U_1 の大小を比較して、遷移確率にしただっがって遷移させる。 （図３右は、遷移せずにとどまった場合を図示したもの）

１番目からＮ番目までの粒子に対して同様の操作を繰り返し行い（１サイクルを 1MC-time とする）、さらに１番目に戻り、定常状態に収束するまで繰り返し行う。

メトロポリス(1次元)にける数値計算

手始めに、１次元の場合について計算し結果を掲載する。 数値計算を行ううえで必要な無次元パラメータを次のように定義する。

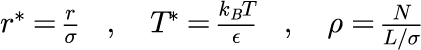
メトロポリスの方法

境界条件なしの場合【C++言語】

/*
メトロポリス(1次元)
境界なし
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string> 
#include "mt19937ar.h"
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;

// 関数のプロトタイプ宣言
double phi_LJ( double r1_1, double r2_1);
//ファイル出力
ofstream ofs1( "ini.data" );
ofstream ofs2( "result.data" );

int main(){
	init_genrand((unsigned)time(NULL));

	int N_p = 100, monte_time=2000;
	double R[100][1] = {0.0};
	double sigma = 1.0, L,T,rho;
	double U_i=0.0, U_k= 0.0;

	rho = 1.0;
	L = N_p/rho;
	T = 1.0;

	for(int n=0; n<N_p; n++){
		R[n][0] = L * genrand_real1();
	}

	for(int n=0; n<N_p; n++){
		ofs1 << R[n][0] << " " << 0 << endl;
	}
	U_i = 0.0;
	for(int i=0; i<N_p-1; i++ ){
		for(int j=i+1; j<N_p; j++ ){
			U_i += 4.0 * phi_LJ(R[i][0],R[j][0]);
		}
	}

	for(int t=0; t<=monte_time;t++){
		cout << t  <<endl;
		for(int n=0;n<N_p;n++){

			double dx = sigma * (1.0 - 2.0 * genrand_real1());
			R[n][0] += dx;
			U_k = 0.0;
			for(int i=0; i<N_p-1; i++ ){
				for(int j=i+1; j<N_p; j++ ){
					U_k += 4.0 * phi_LJ(R[i][0],R[j][0]);
				}
			}
			if(U_i < U_k){
				if(genrand_real1() > pow(e, -(U_k-U_i)/T)){
					R[n][0] -= dx;
				}
			}else{
				U_i = U_k;
			}

		}
		if(t%10 == 0){
			for(int n=0; n<N_p; n++){
			ofs2 << R[n][0] << " " << t << endl;
			}
		}
	}
}
double phi_LJ( double r1_1, double r2_1){
	return  pow(1.0/(r1_1-r2_1),12) - pow(1.0/(r1_1-r2_1),6) ;
}

【計算結果】境界条件なしの場合


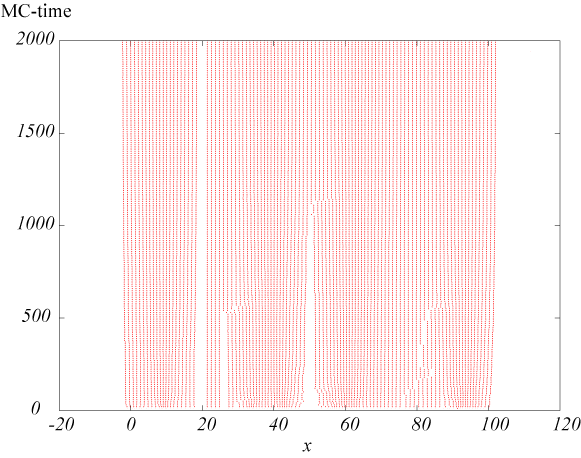
図：\rho = 1.0 の場合


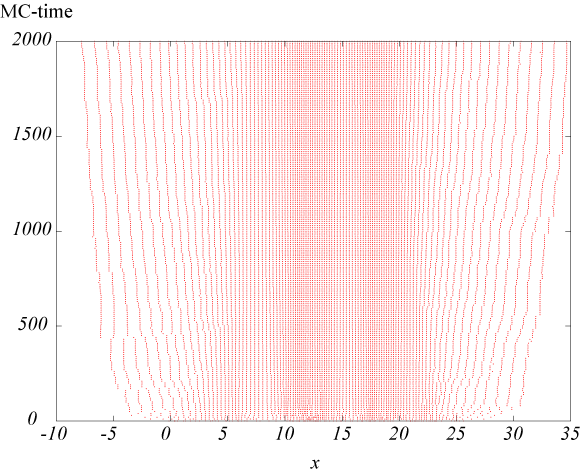
図：\rho = 4.0 の場合

密度が高いほど、ポテンシャルエネルギーは大きな値をとるために、初期配置より外側に離れようとする。 また、弱い引力も働いているために、ある程度より広がらずに一定の状態で落ち着く。

周期的境界条件を課しているの場合【C++言語】

周期的境界条件とは、左の端と右の端をつなぐことである。 境界付近にいる粒子は、反対側の境界付近に存在する粒子からの相互作用を受けると仮定する。 その際の力の切断距離を r_c として計算する。 

/*
メトロポリス(1次元)
周期的境界条件
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string> 
#include "mt19937ar.h"
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;

// 関数のプロトタイプ宣言
double phi_LJ( double r1_1, double r2_1);
//ファイル出力
ofstream ofs1( "ini.data" );
ofstream ofs2( "result.data" );

int main(){
	init_genrand((unsigned)time(NULL));

	int N_p = 100, monte_time=2000;
	double R[100][1] = {0.0};
	double sigma = 1.0, L,T,rho;
	double U_i=0.0, U_k= 0.0;
	double r_c = 5.0;

	rho = 0.9;
	L = N_p/rho;
	T = 1.0;

	for(int n=0; n<N_p; n++){
		R[n][0] = L * genrand_real1();
	}

	for(int n=0; n<N_p; n++){
		ofs1 << R[n][0] << " " << 0 << endl;
	}
	U_i = 0.0;
	for(int i=0; i<N_p-1; i++ ){
		for(int j=i+1; j<N_p; j++ ){
			U_i += 4.0 * phi_LJ(R[i][0],R[j][0]);
		}
		if(R[i][0]<r_c){
			for(int j=0; j<N_p; j++ ){
				U_i += 4.0 * phi_LJ(R[i][0],R[j][0] - L);
			}
		}
		if(L - R[i][0] < r_c){
			for(int j=0; j<N_p; j++ ){
				U_i += 4.0 * phi_LJ(R[i][0],R[j][0] + L);
			}
		}
	}

	for(int t=0; t<=monte_time;t++){
		cout << t  <<endl;
		for(int n=0;n<N_p;n++){

			double dx = sigma/4.0 * (1.0 - 2.0 * genrand_real1());
			R[n][0] += dx;
			if(R[n][0] > L) R[n][0] -= L;
			if(R[n][0] < 0) R[n][0] += L;
			U_k = 0.0;
			for(int i=0; i<N_p-1; i++ ){
				for(int j=i+1; j<N_p; j++ ){
					U_k += 4.0 * phi_LJ(R[i][0],R[j][0]);
				}
				if(R[i][0]<r_c){
					for(int j=0; j<N_p; j++ ){
						U_k += 4.0 * phi_LJ(R[i][0],R[j][0] - L);
					}
				}
				if(L - R[i][0] < r_c){
					for(int j=0; j<N_p; j++ ){
						U_k += 4.0 * phi_LJ(R[i][0],R[j][0] + L);
					}
				}
			}
			if(U_i < U_k){
				if(genrand_real1() > pow(e, -(U_k-U_i)/T)){
					R[n][0] -= dx;
					if(R[n][0] > L) R[n][0] -= L;
					if(R[n][0] < 0) R[n][0] += L;
				}
			}else{
				U_i = U_k;
			}

		}
		//if(t%10 == 0){
			for(int n=0; n<N_p; n++){
			ofs2 << R[n][0] << " " << t << endl;
			}
		//}
	}

}
double phi_LJ( double r1_1, double r2_1){
	return  pow(1.0/(r1_1-r2_1),12) - pow(1.0/(r1_1-r2_1),6) ;
}

【計算結果】周期的境界条件を課した場合


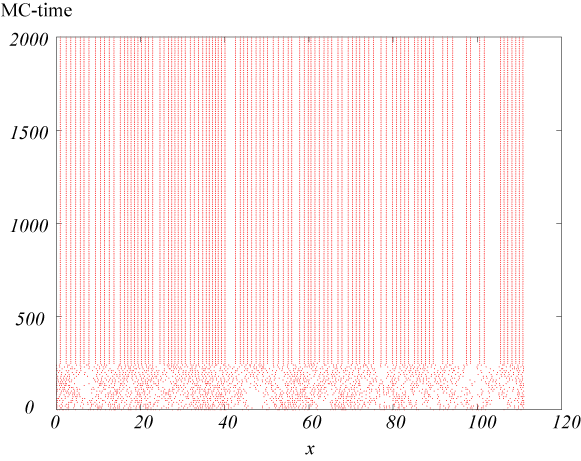
図：\rho = 0.9 の場合

DirectX を利用してのシミュレーション

※Visual C++ 2008 でDirectXを利用する方法はこちらをご覧ください。 

/*
メトロポリス(1次元)
周期的境界条件
*/
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
#include <string> 
#include "mt19937ar.h"
#include "DxLib.h"
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;

ofstream ofs1( "U.data" );
// 関数のプロトタイプ宣言
double phi_LJ( double r1_1, double r2_1);

// プログラムは WinMain から始まります
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
	ChangeWindowMode(TRUE);
	if( DxLib_Init() == -1 ) return -1 ;  // ＤＸライブラリ初期化処理

	int Cr = GetColor(255,255,255); //カラーコードの取得
	DrawBox(20,20,620,440, Cr ,FALSE);
	int fhandle = CreateFontToHandle("MS ゴシック",16, 1, DX_FONTTYPE_EDGE);
	DrawStringToHandle( 10 , 450 , "0" ,Cr, fhandle);
	DrawStringToHandle( 320 , 450 , "x" ,Cr, fhandle);
	DrawStringToHandle( 600 , 450 , "150" ,Cr, fhandle);
	DrawStringToHandle( 10 , 240 , "t" ,Cr, fhandle);
	DrawStringToHandle( 10 , 50 , "400" ,Cr, fhandle);
	//備考：画面サイズはデフォルトで、640×480

	init_genrand((unsigned)time(NULL));

	int N_p = 100, monte_time=2000;
	double R[100][1] = {0.0};
	double sigma = 1.0, L,T,rho;
	double U_i=0.0, U_k= 0.0;
	double r_c = 3.0;

	rho = 0.80;
	L = N_p/rho;
	T = 1.0;

	for(int n=0; n<N_p; n++){
		R[n][0] = L * genrand_real1();
	}

	U_i = 0.0;
	for(int i=0; i<N_p-1; i++ ){
		for(int j=i+1; j<N_p; j++ ){
			U_i += 4.0 * phi_LJ(R[i][0],R[j][0]);
		}
		if(R[i][0]<r_c){
			for(int j=0; j<N_p; j++ ){
				U_i += 4.0 * phi_LJ(R[i][0],R[j][0] - L);
			}
		}
		if(L - R[i][0] < r_c){
			for(int j=0; j<N_p; j++ ){
				U_i += 4.0 * phi_LJ(R[i][0],R[j][0] + L);
			}
		}
	}

	//メインループ
	int t =0 ;
	int tt =1 ;
	while(ProcessMessage()==0 && CheckHitKey(KEY_INPUT_ESCAPE)==0){
				
		for(int n=0;n<N_p;n++){

			double dx = sigma/4.0 * (1.0 - 2.0 * genrand_real1());
			R[n][0] += dx;
			if(R[n][0] > L) R[n][0] -= L;
			if(R[n][0] < 0) R[n][0] += L;
			U_k = 0.0;
			for(int i=0; i<N_p-1; i++ ){
				for(int j=i+1; j<N_p; j++ ){
					U_k += 4.0 * phi_LJ(R[i][0],R[j][0]);
				}
				if(R[i][0]<r_c){
					for(int j=0; j<N_p; j++ ){
						U_k += 4.0 * phi_LJ(R[i][0],R[j][0] - L);
					}
				}
				if(L - R[i][0] < r_c){
					for(int j=0; j<N_p; j++ ){
						U_k += 4.0 * phi_LJ(R[i][0],R[j][0] + L);
					}
				}
			}
			if(U_i < U_k){
				if(genrand_real1() > pow(e, -(U_k-U_i)/T)){
					R[n][0] -= dx;
					if(R[n][0] > L) R[n][0] -= L;
					if(R[n][0] < 0) R[n][0] += L;
				}
			}else{
				U_i = U_k;
			}
			ofs1 << t << " " << U_i << endl;

		}
		for(int n=0; n<N_p; n++){
			DrawPixel( int(R[n][0]*4.0) + 20 , 480 -t -40 ,  Cr ) ;
		}
		if(t>=400){
			t=0;
			tt++;
			ClsDrawScreen();
			DrawBox(20,20,620,440, Cr ,FALSE);
			DrawStringToHandle( 10 , 450 , "0" ,Cr, fhandle);
			DrawStringToHandle( 320 , 450 , "x" ,Cr, fhandle);
			DrawStringToHandle( 600 , 450 , "150" ,Cr, fhandle);
			DrawStringToHandle( 10 , 240 , "t" ,Cr, fhandle);
			DrawStringToHandle( 10 , 50 , "400" ,Cr, fhandle);
		}
		ScreenFlip();
		t++;
	}

	DxLib_End() ;  // ＤＸライブラリ使用の終了処理

	return 0 ;  // ソフトの終了 
}
double phi_LJ( double r1_1, double r2_1){
	return  pow(1.0/(r1_1-r2_1),12) - pow(1.0/(r1_1-r2_1),6) ;
}

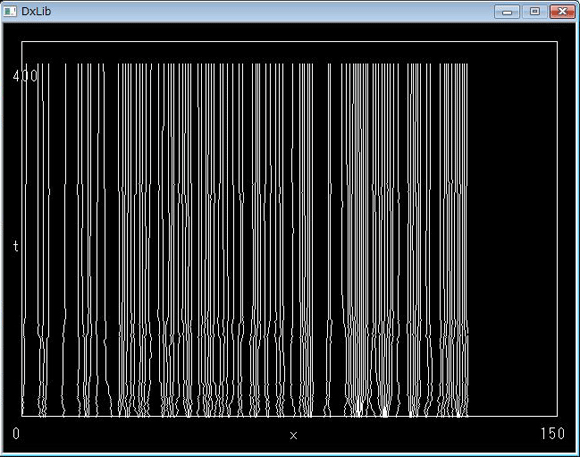
実行結果（Visual C++ 2008 Express Edition）


今後の予定

①ビリアルの定理を利用しての圧力Pの計算
②動径分布の計算
③静的構造因子の計算



▲このページのトップ ｜ NPO法人 natural science トップ

▲このページのトップ ｜ NPO法人 natural science トップ