多細胞生物ボルボックスの議論(東京農工大学物理システム工学科の村山グループ)
議論の背景
東京農工大学物理システム工学科の村山先生と、多細胞生物ボルボックスの議論を行いました。 ボルボックスは多細胞生物のモデル生物で、葉緑体を持ち、光合成することができますが、 繊毛も持ち、光の方向に向かって、泳ぐことができます。 ボルボックスをひとつの粒子とみて、位置、速度という物理的な量を計測することで、 環境に対する応答を調べています。
物理の分野で、花粉などの微粒子がランダムに運動するというブラウン運動が知られています。 アイシュタインは、ブラウン運動が水分子の熱運動の結果として得られることを示しました. この運動は、無生物のランダムな運動ですが、一方、顕微鏡で池の中の微生物を眺めていみると、いろいろな方向に運動していることがわかります。
それでは、生物と無生物の違いとはなんでしょうか? DNAやタンパク質など構成要素に入ることなく、運動を見ただけで生物と無生物の違いを計測できるのでしょうか? 粒子の運動を調べる方法として、速度や位置、速度の相関関数などを調べることができます。 たとえば、ブラウン粒子の移動距離は時間の平方根に比例します。ボルボックスの場合は、どうでしょうか?
ブラウン粒子の場合は、環境の熱揺らぎによって駆動されていますが、 ボルボックスは自発的に揺らぎを発生させ、いろいろな方向に泳いでいます。 また環境からの光刺激に対しては、特定の方向に動くことが必要です。 様々な方向に運動しようする性質と、特定な方向に進もうとする性質を分けて議論することはできないでしょうか?
議論の内容
ボルボックスの運動について、移動距離の時間依存性や、速度分布を求めることで、 熱揺らぎによって駆動される粒子との運動様式を違いを議論した。ボルボックスの遊泳方法について、
- 1. ボルボックスは球形の生き物だが、進行方向に対して、前後がある。
- 2. 前により多く光り感受性が強い細胞が存在する。
- 3. 回転軸のベクトルと進行方向のベクトルが存在する。
- 4. この二つのベクトルの交差の角度によって、個体の運動形態が変わる。
- 5. 運動形態は、らせん状、円弧、直線状などの種類がある。
ボルボックスの揺らぎと刺激に対する応答について、 ブラウン運動を記述するランジュバン方程式(Langevin equation)から、
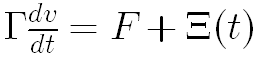
外場の強さと熱揺らぎの大きさに関して、以下の方程式が得られる。 Aは粒子の移動距離である。
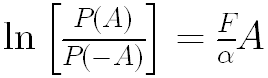
この方程式をボルボックスの運動にあてはめることを考える。 刺激の方向に対するボルボックスの移動量の分布から、左辺の値が求められ、 移動量Aに対して傾きを求めれば、刺激の方向に対する推進力と揺らぎの大きさの比を求めることができる。
ボルボックスの推進力に関しては、ストークスの法則を用いる。 ストークスの法則は、粘性液体中を速さvで進む、半径aの球体が受ける力を表した方程式であるが、 ボルボックスは、一定の速度で進むので、ボルボックスが出す推進力と液体から受ける力は等しいと考えると、 近似的に推進力を測定できる。 以上のように、外場によって駆動させる粒子を自発的に運動する粒子として、よみかえるという操作を行った。
現在、統計的により確からしくするために実験中であるが、 特定方向に進む力と揺らぎの大きさを分離した結果、 環境からの刺激が小さいときは、揺らぎは大きくなり、 刺激がより大きくなった場合は、揺らぎの大きさが一定になることがわかった。 環境からの刺激が大きくなるに従って、揺らぎの大きさを一定にすることで、 特定の方向に向かうことを優先すると考えられる。
参考文献: "Fluctuation Theorem Applied to Dictyostelium discoideum System" K. Hayashi and H. Takagi, Journal of the Physical Society of Japan, Vol. 76, No. 10, October, 2007, 105001























