マンデルブロ集合を描いてみた（VisualC++ ＋ DirectX で描画）

マンデルブロ集合とは

z_n , I を複素数とする。任意の複素数 I に対して、次の漸化式を定義する。

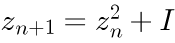　　(1)

但し z_0 = 0 。
n -> \infty の極限で、z_n が有限となる（発散しない） I の集合がマンデルブロ集合（Mandelbrot set）として知られている。
I = x + yi (x,yは実数)と表した場合を図示する。

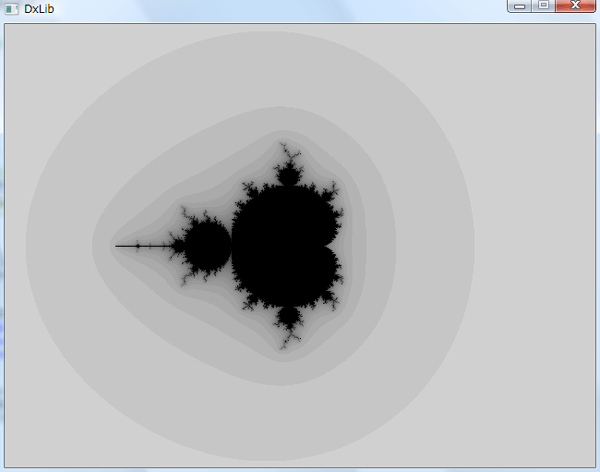
-32<x<32, -24<y<24 の2次元プロット

黒の領域（RGB表記で 0,0,0）は、I に対して、z_n が有限の値に残った領域を表している。
白いほど（RGB表記で 255,255,255 に近いほど）、発散の度合いが強い I であることを意味している。

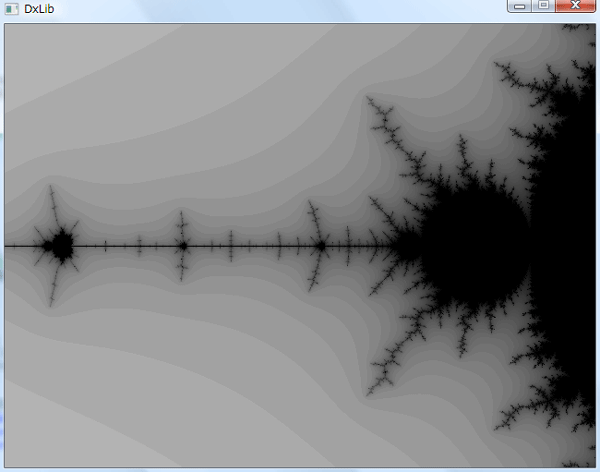
拡大図

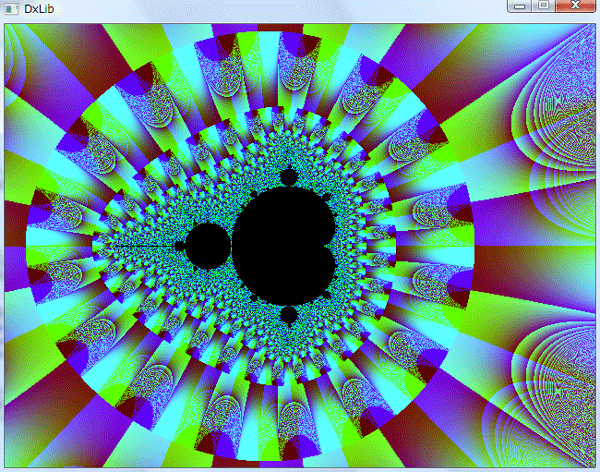
発散時のz_n の 実数部と虚数部の大きさに応じて色分けをした

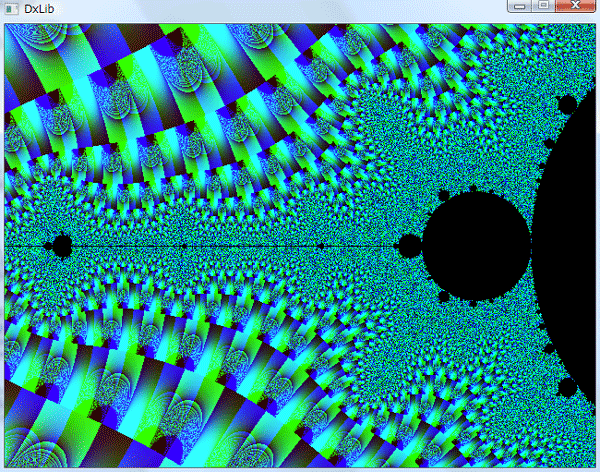
拡大図

VisualC++ ＋ DirectX のソース

DirectXの利用の仕方はこちらをご覧ください。
注意：以下のソースには、無駄なインクルードがあります。

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <complex>

#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <direct.h>
#include "DxLib.h"
using namespace std;

double PI = 3.14159265358979323846;
double e = 2.7182818284590452354;
int width = 640;
int height = 480;
//備考：画面サイズはデフォルトで、640×480

complex<double> Z0,Z1,I;
double broad=100; // 拡大率
int x_0=0; // 描画の中心x座標
int y_0=0; // 描画の中心y座標

// プログラムは WinMain から始まります
int WINAPI WinMain( HINSTANCE hInstance, HINSTANCE hPrevInstance, LPSTR lpCmdLine, int nCmdShow )
{
	int y =-height/2;
	//メインループ
	ChangeWindowMode(TRUE);
	if( DxLib_Init() == -1 ) return -1 ;  // ＤＸライブラリ初期化処理
	while(ProcessMessage()==0 && CheckHitKey(KEY_INPUT_ESCAPE)==0){
//		ClsDrawScreen();
		for(int x = -width/2 ; x <= width/2; x++){
			I = complex<double>(double(x-x_0)/broad,double(y-y_0)/broad);
			Z1 = complex<double>(0,0);
			Z0 = complex<double>(0,0);

			int max=0;
			for(int n=0; n<=1000; n++){
				Z1 = Z0 * Z0 + I;
				if(abs(Z1)>1000000) break;
				Z0 = Z1;
				max++;
			}
			if(max<1000) {
				int r= int(255*pow(e,-double(max)/5.0));
				int g= int(255-255*pow(e,-double(Z0.real())/10000.0));
				int b= int(255-255*pow(e,-double(Z0.imag())/10000.0));
				//printfDx("(%d,%d,%d,%d)\n",x,y,max,g);
				DrawPixel( x+ width/2 , y + height/2 , GetColor(r,g,b)) ;	
			}
		}
		y++;
		if(y>height/2) WaitKey() ;
		ScreenFlip();
	}
	DxLib_End() ;  // ＤＸライブラリ使用の終了処理
	return 0 ;  // ソフトの終了 
}

今後の予定

・さまざまなフラクタルを描いてみる（ジュリア集合など）