VisualC++ と OpenGL を利用した仮想物理実験室
ラグランジュ未定乗数法を用いた球面振子のシミュレーション

ここまでは，拘束条件を取り扱うために一般化座標を導入し， ラグランジュ運動方程式を解くことで単振子のシミュレーションと球面振子のシミュレーションを行ないました。 本節では，拘束条件を別の形で導入して，前回と同様に球面振子のシミュレーションを行ないます。

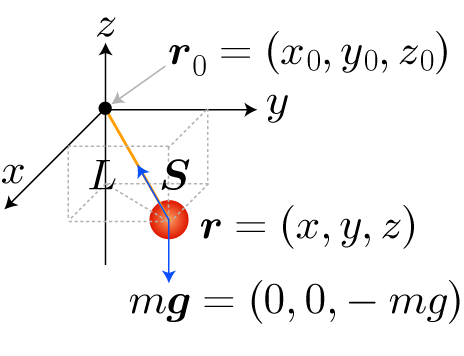
ボールには，重力G と紐に引っ張られる力，張力S の２つの力が働いています。

張力

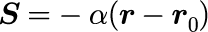
張力は支点(r_0)に向かって，距離に比例した力が加わっていると仮定します。

ボールに加わっている力

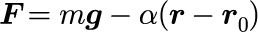
運動方程式

(1)

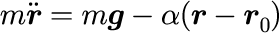
上式の運動方程式にはまだ拘束条件は考えられていません。 αはまだ未知です。

拘束条件

球面振り子の場合には、次の条件が課されます。

(2)

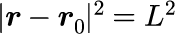
上式の両辺を時間で２回微分します。

(3)

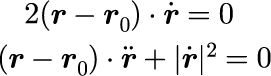
つまり，上記の拘束条件(2)の場合，位置r, 速度 \dot{r}, 加速度 \ddot{r} には上式関係を満たす必要があるということです．

一方，運動方程式(1)の両辺に (r - r_0) の内積をとると

(4)

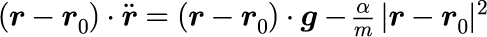
となります。式(3)と(4)からαを決めることができます。

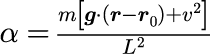
これによりボールの運動を支配する運動方程式が決まります．ただし，v は速度を表します．

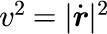
球面振り子の運動方程式

(5)

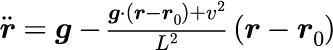
式(5)を用いてシミュレーションするために，シミュレーションを行うため， 数値計算法としてルンゲクッタ法を利用します． ルンゲクッタ法を用いるために，次のように変形します．

(6)

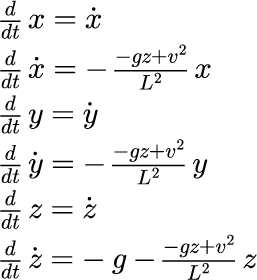
極座標を用いた単振子＋ルンゲクッタ法のアニメーション

極座標を用いた単振子＋ルンゲクッタ法のプログラム

【0-2-3】仮想物理実験室の構築 （ver1.2）を参照ください

構造体の定義

// ボールの定義
double ball_r = 4.0;//ボールの半径
struct BALL {
  double x0, y0, z0;
  double x, y, z;
  double vx, vy, vz;
  double l;
};
const int N = 3;

BALL ball[N];
void SetUp(void){
  for(int i=0; i<N; i++ ){
    ball[i].l  = L;
    ball[i].x0  = 0.0;
    ball[i].y0  = 0.0;
    ball[i].z0  = poll_z;
	  ball[i].x  = ball[i].l;
    ball[i].y  = 0.0;
    ball[i].z  = poll_z;

    ball[i].vx  = 0;
    ball[i].vy  = 10.0 * double(i+1);
    ball[i].vz  = 0;
  }
}

ルンゲクッタ法を利用した数値計算

double fx(double t, double x, double y, double z, double vx, double vy, double vz){
  return vx;
}
double fvx(double t, double x, double y, double z, double vx, double vy, double vz){
	double l2 = pow(x,2)  + pow(y,2)  + pow(z,2);
	double v2 = pow(vx,2) + pow(vy,2) + pow(vz,2);
	return (g*z-v2) * x / l2 ;
}
double fy(double t, double x, double y, double z, double vx, double vy, double vz){
  return vy;
}
double fvy(double t, double x, double y, double z, double vx, double vy, double vz){
	double l2 = pow(x,2)  + pow(y,2)  + pow(z,2);
	double v2 = pow(vx,2) + pow(vy,2) + pow(vz,2);
	return (g*z-v2) * y / l2 ;
}
double fz(double t, double x, double y, double z, double vx, double vy, double vz){
  return vz;
}
double fvz(double t, double x, double y, double z, double vx, double vy, double vz){
	double l2 = pow(x,2)  + pow(y,2)  + pow(z,2);
	double v2 = pow(vx,2) + pow(vy,2) + pow(vz,2);
	return -g + (g*z-v2) * z / l2 ;
}
void RungeKutta4(BALL *ball){
  double k1[6],k2[6],k3[6],k4[6];
  double x  = ball -> x - ball -> x0;
  double vx = ball -> vx;
  double y  = ball -> y - ball -> y0;
  double vy = ball -> vy;
  double z  = ball -> z - ball -> z0;
  double vz = ball -> vz;

  k1[0]=dt*fx(t,x,y,z,vx,vy,vz);
  k1[1]=dt*fvx(t,x,y,z,vx,vy,vz);
  k1[2]=dt*fy(t,x,y,z,vx,vy,vz);
  k1[3]=dt*fvy(t,x,y,z,vx,vy,vz);
  k1[4]=dt*fz(t,x,y,z,vx,vy,vz);
  k1[5]=dt*fvz(t,x,y,z,vx,vy,vz);
  k2[0]=dt*fx(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k2[1]=dt*fvx(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k2[2]=dt*fy(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k2[3]=dt*fvy(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k2[4]=dt*fz(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k2[5]=dt*fvz(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
  k3[0]=dt*fx(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k3[1]=dt*fvx(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k3[2]=dt*fy(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k3[3]=dt*fvy(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k3[4]=dt*fz(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k3[5]=dt*fvz(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
  k4[0]=dt*fx(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  k4[1]=dt*fvx(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  k4[2]=dt*fy(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  k4[3]=dt*fvy(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  k4[4]=dt*fz(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  k4[5]=dt*fvz(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
  ball->x  = ball->x  + (k1[0]+2.0*k2[0]+2.0*k3[0]+k4[0])/6.0;
  ball->vx = ball->vx + (k1[1]+2.0*k2[1]+2.0*k3[1]+k4[1])/6.0;
  ball->y  = ball->y  + (k1[2]+2.0*k2[2]+2.0*k3[2]+k4[2])/6.0;
  ball->vy = ball->vy + (k1[3]+2.0*k2[3]+2.0*k3[3]+k4[3])/6.0;
  ball->z  = ball->z  + (k1[4]+2.0*k2[4]+2.0*k3[4]+k4[4])/6.0;
ball->vz = ball->vz + (k1[5]+2.0*k2[5]+2.0*k3[5]+k4[5])/6.0;
}