【波動論４】
デルタ関数の定義

デルタ関数は次の式で定義される関数です。

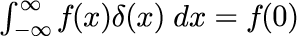
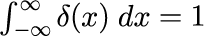
デルタ関数は我々がよく知っている関数を利用して近似することができます。

sin関数を利用した場合

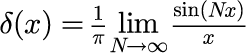
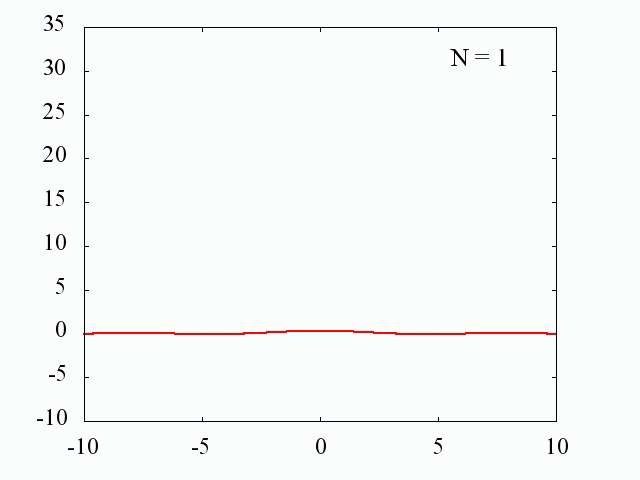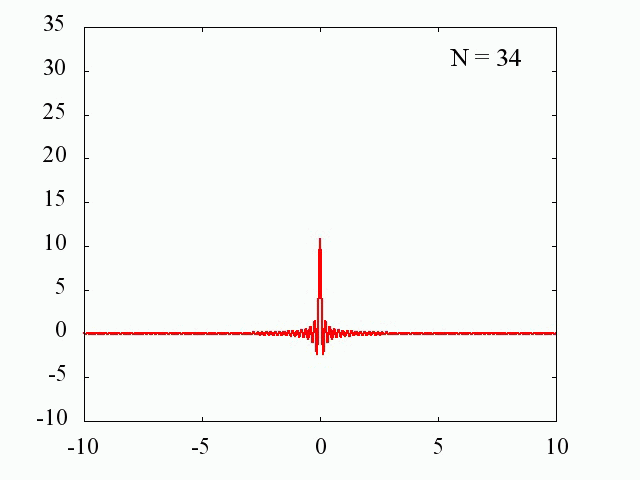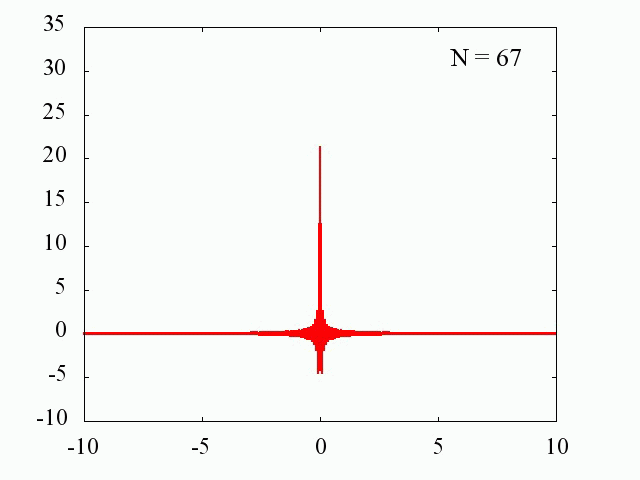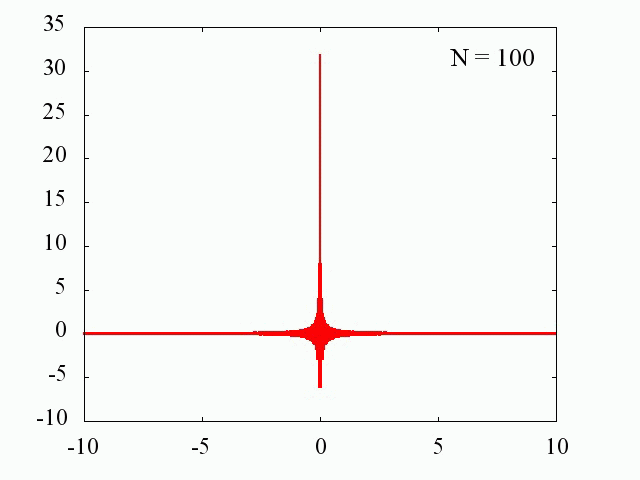
ガウス分布を利用した場合

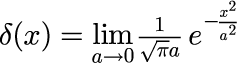
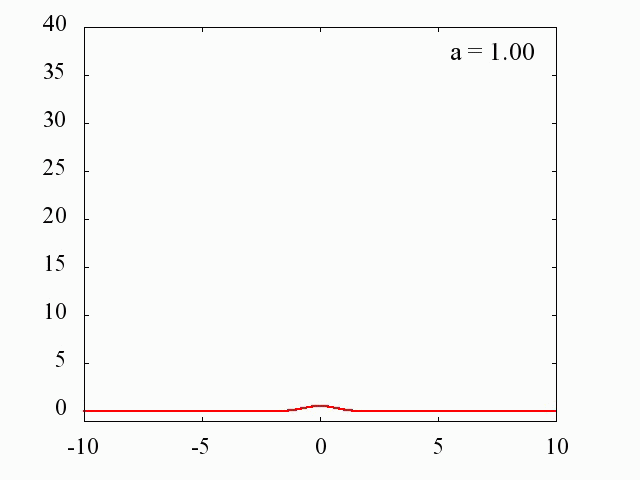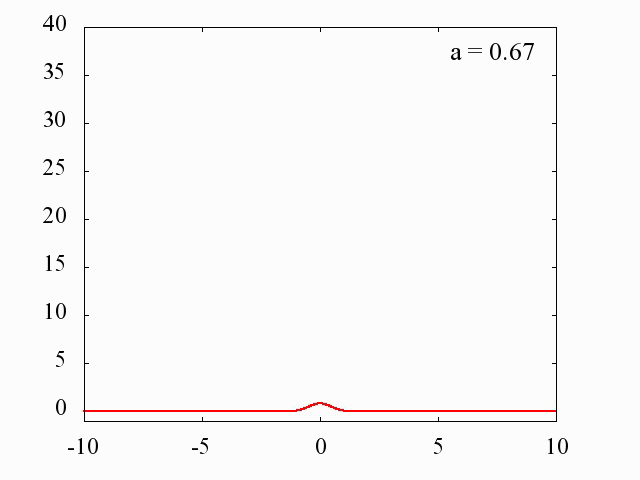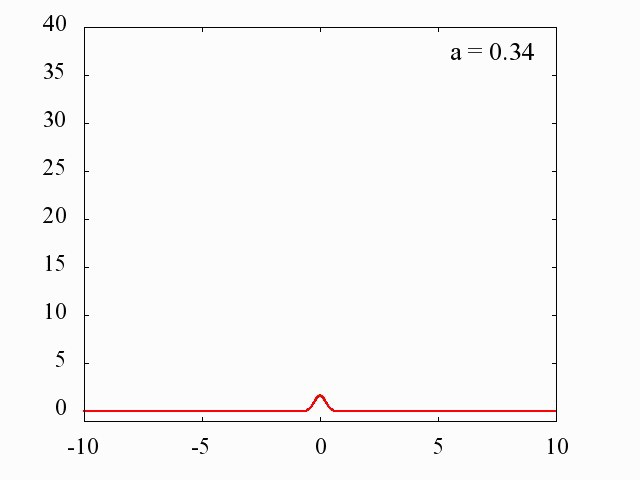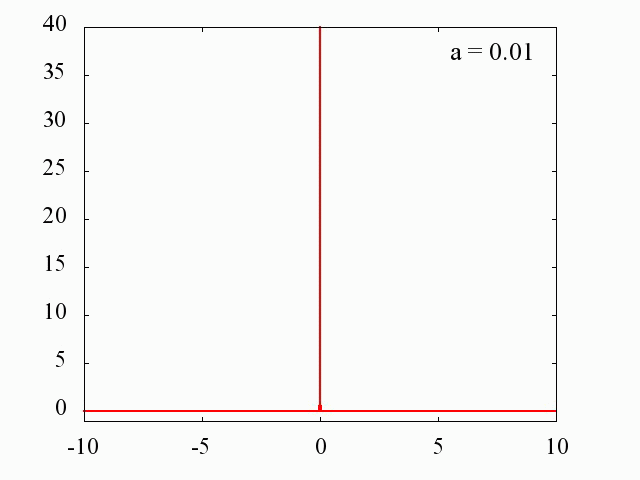
C++ プログラム

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);
int xN =2000;
int N = 10;
double dx = 0.01;
char str[100];
string folder = "2", ff="", fg="";  //保存フォルダ名
ostringstream fname;
double F1(double x, int n);
double F2(double x, double a);

int main(){
 _mkdir(folder.c_str());
    for(int i=1; i<=100; i++){
      sprintf_s( str ,"%d.data",i);
      ff = folder + "/" + string(str);
      ofstream fout_Psi;
      fout_Psi.open(ff.c_str());
      for(int j=0; j<=xN; j++){
        double x = dx * double(j-xN/2);
        fout_Psi << x << " " << F1(x, i) << endl;
      }
      fout_Psi.close();
    }
/*
   for(int i=1; i<=100; i++){
      double a = 1.0 - double(i-1)/100.0;
      sprintf_s( str ,"%d.data",i);
      ff = folder + "/" + string(str);
      ofstream fout_Psi;
      fout_Psi.open(ff.c_str());
      for(int j=0; j<=xN; j++){
        double x = dx * double(j-xN/2);
        fout_Psi << x << " " << F2(x, a) << endl;
      }
      fout_Psi.close();
    }
*/
  return 0;
}
double F1(double x, int n){
  if(x==0.0) return double(n)/PI;
  else return sin(double(n)*x)/x/PI;
}
double F2(double x, double a){
  return exp(-pow(x,2)/pow(a,2))/(sqrt(PI)*a);
}

gnuplot テンプレート

set terminal jpeg  enhanced font "Times" 20
set tics font 'Times,18'
set rmargin 3
set lmargin 3
set nokey
set yr[-1:40]

if (exist("n")==0 || n<0) n=1 #変数の初期化

file0(n) = sprintf("2/%d.data",n)                #入力ファイル名
outfile(n) = sprintf("2-/%d.jpg",n+10000)        #出力ファイル名
#title(n) = sprintf("N = %d",n)                  #タイトル名
title(n) = sprintf("a = %3.2f",1.0-(n-1)/100.0)  #タイトル名

unset label 
set label title(n)  font 'Times,20'  at 5.5 , 37

set output outfile(n)
plot file0(n) u 1:2 w l lw 2 

if (n<100)  n=n+1; reread