VisualC++ と OpenGL を利用した仮想物理実験室
2体問題のシミュレーション(C言語+ルンゲクッタ法)
天体の重力を利用して方向を変化させる「スイングバイ」という技術があります。 今年の暮れに話題になった「はやぶさ」「あかつき」などの惑星探査機も、「スイングバイ」を多様したようです。宇宙航空研究開発機構のWEBページ上では「「はやぶさ」地球スイングバイの実施と結果について」と題して、はやぶさが地球を利用して行ったスイングバイの結果が詳細に紹介されています。
スイングバイのシミュレーションの前座として、今回は2体問題をシミュレーションします。
質量m_1,m_2の2つの物体が距離の逆2乗で引き合う(-a/r^2)場合を考えます。 初期状態として、下の図のように初速度0の「物体1」が原点、 x軸上にいる「物体2」がy軸方向への初速度 v_0 であるとします。
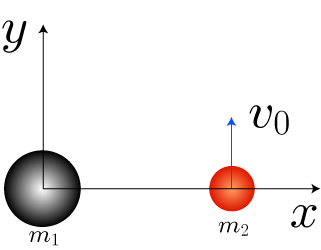
2体問題では、初期値の値によって運動が大きくは3パターンに分けられます。
1.もつれ合いながらの楕円的運動
2.等速度円運動
3.無限遠に離れていく運動
具体的にラグランジュ運動方程式からの導出は次回行うとして、今回はシミュレーションの結果と、C言語のプログラムを紹介します。
シミュレーション結果
OpenGL での描画は、2体の重心を中心にしています。
下の(x,y)は重心の位置を表し、L は2体間の距離を表しています。
初速度が小さい場合

初速度が等速円運動の条件を満たす場合

初速度が大きくなって、無限遠に飛ぶよりも少し小さい場合

初速度がもっと大きくなって、無限遠に飛ぶ条件を満たした場合

C++プログラム
//////////////////////////////////////////////////////////////////////////
// 2体問題
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <direct.h>
#include <time.h>
using namespace std;
double PI = acos(-1.0);
//////////////////////////////////////////////////////////////////////////
// 変数の定義
//////////////////////////////////////////////////////////////////////////
ofstream file1( "2body_55.data" );//<------出力ファイル名
//--------------------------------------------------------
// 仮想物理実験室変数の定義
//--------------------------------------------------------
double t = 0.0; //時刻
double t_end = 3000.0;//計算を終了する時刻
double dt= 0.001; //時間刻み
int skipDat = 1000; //データ書出し回数の間引き回数
double R[3]; //重心座標(座標の原点)
double theta = PI * 3.0/6.0;//初期x軸とのなす角
double v2_0 = sqrt(55.0/200.0); //初速度
//E=0(無限遠まで) v2_0 = sqrt(220.0/200.0);
//E=Emin(円運動) v2_0 = sqrt(110.0/200.0);
//E_min<E<0(楕円運動) v2_0 = sqrt(55.0/200.0);
double r0 = 20.0; //初期2点間の距離
double a = 10.0; //F(r)=-a/r^2
double L12 =r0; //2点間の距離
struct BALL {
double m; //ボールの質量
double r; //ボールの半径
double x, y, z;
double vx, vy, vz;
};
BALL ball1, ball2;
void SetUp(void){
ball1.r = 4.0;
ball1.m = 10.0;
ball1.x = 0.0;
ball1.y = 0.0;
ball1.z = 0.0;
ball1.vx = 0.0;
ball1.vy = 0.0;
ball1.vz = 0.0;
ball2.r = 2.0;
ball2.m = 1.0;
ball2.x = r0;
ball2.y = 0.0;
ball2.z = 0.0;
ball2.vx = v2_0 * cos(theta);
ball2.vy = v2_0 * sin(theta);
ball2.vz = 0.0;
R[0] = (ball1.m * ball1.x +ball2.m * ball2.x)/(ball1.m+ball2.m) ;
R[1] = (ball1.m * ball1.y +ball2.m * ball2.y)/(ball1.m+ball2.m) ;
R[3] = (ball1.m * ball1.z +ball2.m * ball2.z)/(ball1.m+ball2.m) ;
}
//////////////////////////////////////////
// ルンゲクッタ用
void RungeKutta4(BALL ball1[], BALL ball2[]);
void Calculate();
int main(){
SetUp();
for(int tn=0; tn <= int(t_end/dt) ;tn++){
t =dt* tn;
Calculate();
if(tn%skipDat == 0){
file1 << t << " " << L12 << endl;
}
}
return 0;
}
//--------------------------------------------------------
// 計算と物体の描画
//--------------------------------------------------------
void Calculate(){
RungeKutta4( &ball1, &ball2);
R[0] = (ball1.m * ball1.x +ball2.m * ball2.x)/(ball1.m+ball2.m) ;
R[1] = (ball1.m * ball1.y +ball2.m * ball2.y)/(ball1.m+ball2.m) ;
R[3] = (ball1.m * ball1.z +ball2.m * ball2.z)/(ball1.m+ball2.m) ;
L12 = sqrt(pow(ball2.x-ball1.x,2)+pow(ball2.y-ball1.y,2)+pow(ball2.z-ball1.z,2));
}
/////////////////////////////////////////////
// ルンゲクッタ
double fx1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vx1;
}
double fy1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vy1;
}
double fz1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vz1;
}
double fvx1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return a/m1 * (x2-x1) / pow(L12 ,3);
}
double fvy1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return a/m1 * (y2-y1) / pow(L12 ,3);
}
double fvz1(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return a/m1 * (z2-z1) / pow(L12 ,3);
}
double fx2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vx2;
}
double fy2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vy2;
}
double fz2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
return vz2;
}
double fvx2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return - a/m2 * (x2-x1) / pow(L12 ,3);
}
double fvy2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return - a/m2 * (y2-y1) / pow(L12 ,3);
}
double fvz2(double t, double m1, double x1, double y1, double z1, double vx1, double vy1, double vz1, double m2, double x2, double y2, double z2, double vx2, double vy2, double vz2){
double L12 = sqrt(pow(x2-x1,2)+pow(y2-y1,2)+pow(z2-z1,2));
return - a/m2 * (z2-z1) / pow(L12 ,3);
}
void RungeKutta4(BALL *ball1, BALL *ball2){
double k1[2][6],k2[2][6],k3[2][6],k4[2][6];
double x1 = ball1 -> x;
double vx1 = ball1 -> vx;
double y1 = ball1 -> y;
double vy1 = ball1 -> vy;
double z1 = ball1 -> z;
double vz1 = ball1 -> vz;
double m1 = ball1 -> m;
double x2 = ball2 -> x;
double vx2 = ball2 -> vx;
double y2 = ball2 -> y;
double vy2 = ball2 -> vy;
double z2 = ball2 -> z;
double vz2 = ball2 -> vz;
double m2 = ball2 -> m;
k1[0][0]=dt*fx1( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[0][1]=dt*fvx1(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[0][2]=dt*fy1( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[0][3]=dt*fvy1(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[0][4]=dt*fz1( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[0][5]=dt*fvz1(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][0]=dt*fx2( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][1]=dt*fvx2(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][2]=dt*fy2( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][3]=dt*fvy2(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][4]=dt*fz2( t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k1[1][5]=dt*fvz2(t,m1,x1,y1,z1,vx1,vy1,vz1,m2,x2,y2,z2,vx2,vy2,vz2);
k2[0][0]=dt*fx1( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[0][1]=dt*fvx1(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[0][2]=dt*fy1( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[0][3]=dt*fvy1(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[0][4]=dt*fz1( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[0][5]=dt*fvz1(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][0]=dt*fx2( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][1]=dt*fvx2(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][2]=dt*fy2( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][3]=dt*fvy2(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][4]=dt*fz2( t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k2[1][5]=dt*fvz2(t+dt/2.0,m1,x1+k1[0][0]/2.0,y1+k1[0][2]/2.0,z1+k1[0][4]/2.0,vx1+k1[0][1]/2.0,vy1+k1[0][3]/2.0,vz1+k1[0][5]/2.0, m2,x2+k1[1][0]/2.0,y2+k1[1][2]/2.0,z2+k1[1][4]/2.0,vx2+k1[1][1]/2.0,vy2+k1[1][3]/2.0,vz2+k1[1][5]/2.0);
k3[0][0]=dt*fx1( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[0][1]=dt*fvx1(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[0][2]=dt*fy1( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[0][3]=dt*fvy1(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[0][4]=dt*fz1( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[0][5]=dt*fvz1(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][0]=dt*fx2( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][1]=dt*fvx2(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][2]=dt*fy2( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][3]=dt*fvy2(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][4]=dt*fz2( t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k3[1][5]=dt*fvz2(t+dt/2.0,m1,x1+k2[0][0]/2.0,y1+k2[0][2]/2.0,z1+k2[0][4]/2.0,vx1+k2[0][1]/2.0,vy1+k2[0][3]/2.0,vz1+k2[0][5]/2.0 ,m2,x2+k2[1][0]/2.0,y2+k2[1][2]/2.0,z2+k2[1][4]/2.0,vx2+k2[1][1]/2.0,vy2+k2[1][3]/2.0,vz2+k2[1][5]/2.0);
k4[0][0]=dt*fx1( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[0][1]=dt*fvx1(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[0][2]=dt*fy1( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[0][3]=dt*fvy1(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[0][4]=dt*fz1( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[0][5]=dt*fvz1(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][0]=dt*fx2( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][1]=dt*fvx2(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][2]=dt*fy2( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][3]=dt*fvy2(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][4]=dt*fz2( t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
k4[1][5]=dt*fvz2(t+dt/2.0,m1,x1+k3[0][0],y1+k3[0][2],z1+k3[0][4],vx1+k3[0][1],vy1+k3[0][3],vz1+k3[0][5] ,m2,x2+k3[1][0],y2+k3[1][2],z2+k3[1][4],vx2+k3[1][1],vy2+k3[1][3],vz2+k3[1][5]);
ball1->x = ball1->x + (k1[0][0]+2.0*k2[0][0]+2.0*k3[0][0]+k4[0][0])/6.0;
ball1->vx = ball1->vx + (k1[0][1]+2.0*k2[0][1]+2.0*k3[0][1]+k4[0][1])/6.0;
ball1->y = ball1->y + (k1[0][2]+2.0*k2[0][2]+2.0*k3[0][2]+k4[0][2])/6.0;
ball1->vy = ball1->vy + (k1[0][3]+2.0*k2[0][3]+2.0*k3[0][3]+k4[0][3])/6.0;
ball1->z = ball1->z + (k1[0][4]+2.0*k2[0][4]+2.0*k3[0][4]+k4[0][4])/6.0;
ball1->vz = ball1->vz + (k1[0][5]+2.0*k2[0][5]+2.0*k3[0][5]+k4[0][5])/6.0;
ball2->x = ball2->x + (k1[1][0]+2.0*k2[1][0]+2.0*k3[1][0]+k4[1][0])/6.0;
ball2->vx = ball2->vx + (k1[1][1]+2.0*k2[1][1]+2.0*k3[1][1]+k4[1][1])/6.0;
ball2->y = ball2->y + (k1[1][2]+2.0*k2[1][2]+2.0*k3[1][2]+k4[1][2])/6.0;
ball2->vy = ball2->vy + (k1[1][3]+2.0*k2[1][3]+2.0*k3[1][3]+k4[1][3])/6.0;
ball2->z = ball2->z + (k1[1][4]+2.0*k2[1][4]+2.0*k3[1][4]+k4[1][4])/6.0;
ball2->vz = ball2->vz + (k1[1][5]+2.0*k2[1][5]+2.0*k3[1][5]+k4[1][5])/6.0;
}
次回はラグランジュ運動方程式から出発して、2体問題と等価な1対問題への帰着から、各種条件の導出までを行います。
























