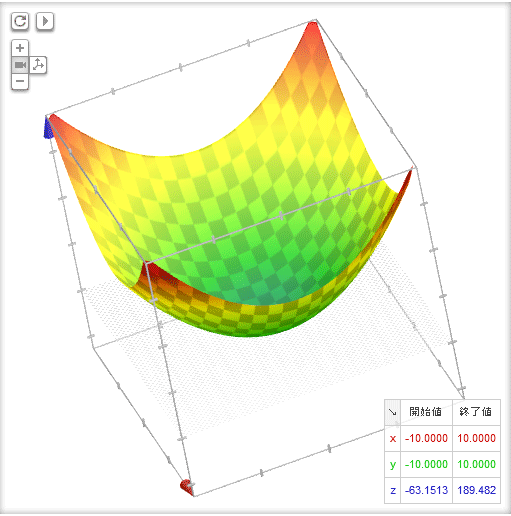
クォータニオンによる視点の移動 （WebGL（Three.js））

３次元空間中の物体を任意の軸に対して、任意の角度回転させることを考えます。 これは、コンピュータグラフィックなどの世界で、マウス操作などの入力装置を利用して３次元の物体の向きを変更させたいときに必須となります。 一般的に「回転」といえば「オイラー角」を思い浮かべるわけですが、任意の軸に対する回転は不得意であることが知られています。 それは、任意の軸に対する回転に対応する３つのオイラー角が直感的には定式化できないためです。 また、場合によってはジンバルロックと呼ばれるオイラー角を利用時に特定の条件で発生する特有の問題もあります。 そこで、コンピュータグラフィックなどで、任意の軸に対する回転を演算する際に、「クォータニオン（四元数）」と呼ばれる複素数の拡張版のような代数が利用されます。 本稿では、3次元グラフィック技術である WebGL（Three.js）にて視点をマウスで自由自在に移動することを目的に、 クォータニオンを Javascript で演算することを行います。

任意の軸に対する回転

次の図のような、座標にある物体を、回転軸ベクトルに対して角度回転させた後の座標をとなる場合を考えます。

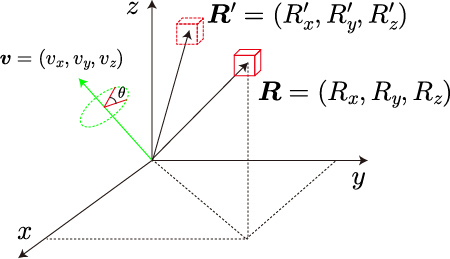
この回転は、回転軸ベクトル（３自由度）と回転角（１自由度）の４つのパラメータで指定することができます。 クォータニオンを利用すると、はに対して２回の演算で計算することができます。 具体的な演算方法は「７０秒で分る、使える、四元数・４元数・クォータニオン・ Quaternionで回転 （中田亨氏）」をご覧ください。ウェブページのタイトル通り確かに70秒で計算できました。

Javascriptによるクォータニオンを利用した回転の演算

クォータニオンはコンピュータグラフィックで非常によく利用されるため、クォータニオン演算のためのライブラリも存在します。 今回は、WebGL を使用する時に必要となる行列計算を、簡単に演算することのできる「glMatrix.js」を利用します。この中でクォータニオンの演算も定義されています。

glMatrix.jsでクォータニオンの演算

glMatrix.js でクォータニオンは

var P = new quat4.create([x,y,z,w]);

で定義することができます。x,y,z は、クォータニオンの i,j,k の係数を表し、w がクォータニオンの実数部を表します。 2つのクォータニオンの積は

var P = new quat4.create([x1,y1,z1,w1]);
var Q = new quat4.create([x2,y2,z2,w2]);
var R = quat4.multiply(P,Q, quat4.create());

で計算することできます。

クォータニオンを利用した回転の計算

座標ベクトル v = [vx, vy, vz] を 任意の回転軸 u = [ux, uy, uz]に対して、角度 theta 回転させた後の座標ベクトルを計算する関数を定義します。

function QuaternionRotation(theta, u, v){ //(回転角, 回転軸, 座標ベクトル)
  var P = new quat4.create([v[0],v[1],v[2],0]);
  var Q = new quat4.create([-u[0]*Math.sin(theta/2), -u[1]*Math.sin(theta/2), -u[2]*Math.sin(theta/2), Math.cos(theta/2)]);
  var R = new quat4.create([u[0]*Math.sin(theta/2), u[1]*Math.sin(theta/2), u[2]*Math.sin(theta/2), Math.cos(theta/2)]);
  var S0 = quat4.multiply(P,Q, quat4.create());
  var S =  quat4.multiply(R,S0,quat4.create());  
  var V = [S[0],S[1],S[2]];
  return V;
}

この関数を利用することで、簡単に回転後の座標を計算することができます。

視点のマウスによる移動

2012年3月に google が WebGL を利用したアプリケーションが注目を集めています。 google の検索窓に「z=x^2+y^2」などと入力すると、3次元グラフを描画することができ、マウスグラックを利用して視点自在に移動することができます。 下図はその3次元グラフのキャプチャです。

視点の移動は、マウスクリック時のマウスポインタの座標を基準として、 視点の位置ベクトルと視点の上の向きを表すベクトルが、マウスの移動量 dx, dy に応じて変更することで実現することができます。 本稿では、上記のクォータニオンを利用して、2次元平面の canvas 上をマウスドラックすることで視点の移動させることを考えます。

視点移動の模式図

canvas 上を横方向（移動量 dx）と縦方向（移動量 dy）にマウスドラックさせることで視点を回転させることを考えます。 ただし、視点は原点（0,0,0）を向いているとします。 一般に視点の自由度は、視点の位置ベクトル（3自由度）と視点の上の向きを表すベクトル（3自由度）の計6自由度ですが、視点は原点（0,0,0）を向いていると条件を課すと、視点の上の向きを表すベクトルは位置ベクトルと垂直となり、実質的には１自由度となりますが、 演算の都合上ベクトルで表しておきます。

次に、マウスの移動量 dx, dy と具体的な視点の移動量との関係を、視点の位置ベクトルと上向きベクトルから一意に決定する軸による回転として得られると考えます。 視点の位置ベクトル（）と上向きベクトル（）に対する回転軸の模式図は次図のとおりです。

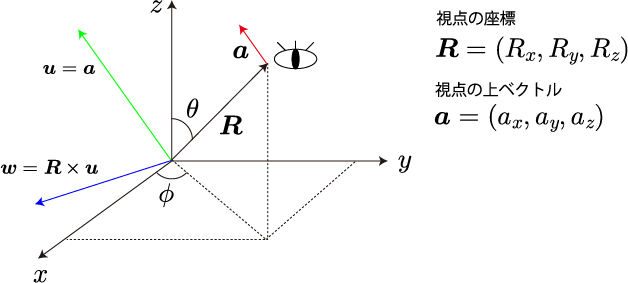
dx に対しては（緑）軸回転、dy に対しては（青）軸回転に対応させます。 図でも示しているとおり、とから上記の２軸は、 、と簡単に計算することができます。ここまでくればあとは前節で触れたクォータニオンを利用して軸回転後の座標を計算することで、回転後の視点の位置ベクトルがわかります。 本稿では次のステップで計算します。

１．クリック時の視点の位置ベクトル、視点の上向きベクトルを取得する。
２．とから、２つの回転軸ベクトル,を計算する。
３．マウス移動量 dx, dy から回転角度、を計算する。
４．クォータニオンを利用して、, 軸周りに、回転後の位置ベクトルを計算する。
５．クォータニオンを利用して、視点の上方向ベクトルを計算する。

次は、本稿で作成した視点の移動のサンプルです。

クオータニオンを用いた視点の移動テスト

HTML5 canvas 要素の WebGL（Three.jsライブラリ）を用いて、表題のテストを行います。 WebGLを利用可能な環境で下のフレーム内の図をドラックしてみてください。 視点を移動することができます。

※上記のサンプルプログラムは、HTML5 のcanvas 要素を利用した WebGL を簡単に利用するためのライブラリである Three.js を利用しています。

１．クリック時の視点の位置ベクトル、視点の上向きベクトルを取得する。

R = new vec3.create([camera.position.x,camera.position.y,camera.position.z]); // 視点の位置ベクトルの取得
a = new vec3.create([camera.up.x, camera.up.y, camera.up.z]);                 // 視点の上向きベクトルの取得

ただし、vec3 は glMatrix.js で定義されている３次元ベクトルです。 とが得られました。

２．とから、２つの回転軸ベクトル,を計算する。

u = vec3.set(a, vec3.create());       // a のコピー
u = vec3.normalize(u, vec3.create()); // u の規格化
w = vec3.cross(R, u ,vec3.create());  // R × u の演算
w = vec3.normalize(w, vec3.create()); // w の規格化

glMatrix.js には vec3 で定義された３次元ベクトルの演算が定義されています。
上記は「vec3.set：コピー」「vec3.normalize：規格化」「vec3.cross：外積」を意味します。 この他にも、必要な演算が定義されています。

３．マウス移動量 dx, dy から回転角度、を計算する。

theta_u =  dx / 100;
theta_w = -dz / 100;

これは適当に決めます。もし、マウスの移動量に対して速く回転させたければ、100 → 50 とし、逆に遅くしたければ 100 → 200 としてください。

４．クォータニオンを利用して、, 軸周りに、回転後の位置ベクトルを計算する。

視点の位置ベクトルを、回転軸ベクトルで回転後、 さらにで回転させます。

S = QuaternionRotation(theta_u, u, [camera.position.x, camera.position.y, camera.position.z]);
S = QuaternionRotation(theta_w, w, [S[0],S[1],S[2]]);

５．クォータニオンを利用して、視点の上方向ベクトルを計算する。

４までで視点の移動は完了していますが、このままでは「google 3Dグラフ」のような操作性は実現できません。 上の模式図を見ればわかりますが、回転軸で視点を回転させると、視点の上ベクトルも回転することがわかります。つまり、

S = QuaternionRotation(theta_w, w, [camera.up.x,camera.up.y,camera.up.z]);
camera.up.set(S[0],S[1],S[2]);

で視点の上ベクトルを計算することができます。 本稿では、クオータニオンを用いて視点の回転を計算しましたが、物体そのもの姿勢制御でもクオータニオンはオイラー角に比べて簡単に実装することができます。また、以上の計算は、WebGLだけでなくどのようなプログラムにも適用することができます。 今回はこんな程度で終わりにします。