HOME > natural science Laboratory > コンピュータ・シミュレーション講座 > ゼロから作るDeep Learning

【量子力学再入門2】
自由空間中の相互作用しない量子粒子２個の運動

文責：遠藤 理平 （2018年4月21日） カテゴリ：ゼロから作るDeep Learning(49)

　量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。 メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。第一のテーマとして、下の図のような量子粒子の衝突をシミュレーションします。

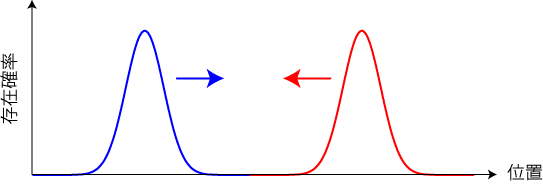
量子力学における粒子（量子粒子）は確率振幅と呼ばれる波で表されます。また、量子粒子は同じ種類の粒子の場合には衝突の前後で粒子の見分けがつかないという特徴があります。 前回は量子粒子１個の運動をシミュレーションしました。次に自由空間中の相互作用しない量子粒子２個の運動をシミュレーションします。


自由空間の量子粒子の運動

位置表示のハミルトニアン

自由空間中の相互作用しない量子粒子２個に対応するハミルトニアンは次のとおりです。

{\cal H} (\mathbf{x}_1,\mathbf{x}_2 ) = -\frac{\hbar^2}{2m} \nabla_1^2 -\frac{\hbar^2}{2m} \nabla_2^2

このハミルトニアンは\mathbf{x}_1, \mathbf{x}_2を分離することができるので、解はそれぞれの位置変数に対する解の積で表されます。同種粒子の波動関数は対称あるいは反対称を取る必要があるため、波動関数の位置依存性は以下の通りになります。

\psi (\mathbf{x}_1,\mathbf{x}_2;t )= \frac{1}{\sqrt{2}} \left[ \varphi_1(\mathbf{x}_1,t)\varphi_2(\mathbf{x}_2,t) \pm \varphi_1(\mathbf{x}_2,t)\varphi_2(\mathbf{x}_1,t) \right]

「＋」符号は対称、「－」は反対称の波動関数を表します。なお、各位置変数に対する解と分散関係は以下のとおりです。

\varphi_1(\mathbf{x}_1,t) =\sum\limits_{n_1} c_{n_1} e^{i\mathbf{k}_{n_1}\cdot\mathbf{x}_{1}} e^{-i\omega_{n_1}t}
\varphi_2(\mathbf{x}_2,t) =\sum\limits_{n_2} c_{n_2} e^{i\mathbf{k}_{n_2}\cdot\mathbf{x}_{2}} e^{-i\omega_{n_2}t}

E_{n_1} =\hbar \omega_{n_1} = \frac{\hbar^2k_{n_1}^2}{2m} , E_{n_2} =\hbar \omega_{n_2} = \frac{\hbar^2k_{n_2}^2}{2m}

このc_{n_1}, c_{n_2}を前項と同じガウシアンとすることで、２つの波束を運動させることができます。

粒子の確率密度の定義

ある位置\mathbf{x}に粒子１あるいは粒子２が存在する確率密度を次のとおりに定義します。

\rho(\mathbf{x},t)= \rho_1(\mathbf{x},t) + \rho_2(\mathbf{x},t)

ただし、

\rho_1(\mathbf{x},t) = \int |\psi(\mathbf{x},\mathbf{x}_2;t)|^2 d\mathbf{x}_2
\rho_2(\mathbf{x},t) = \int |\psi(\mathbf{x}_1,\mathbf{x};t)|^2 d\mathbf{x}_1

です。

シミュレーション結果

初期状態として左から右向きに運動する波束と原点で静止した波束を配置した結果（対称の波動関数）です。相互作用が無いため、そのまますり抜けます。
なお、反対称波動関数の場合でも結果は変わりません。

計算パラメータ

波束の中心エネルギー（左波束）：E0 = 10.0 * eV;
空間スケール 1E-11[m];//横軸の値
時間スケール 1E-16[s];//動画１コマの時間間隔


考察と次の課題

・相互作用の無い２粒子の運動は問題なく計算できているように思える。
・対称波動関数と反対称波動関数で結果が同じになるのはちょっと意外だった。
・また、\rho_1と\rho_2も同じ空間分布となった。
→ 粒子の区別は本質的に不可能であることをを意味していると考えられる、
→ 解釈が間違っていたらご指摘ただければ幸いです。
・２粒子に相互作用を加えた途端、波動方程式の解は単純な積では与えられず簡単には得られなくなるので、シュレディンガー方程式そのものの数値解を得る必要がある。
→ もっと基礎的な系から順番にやっていく。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics2.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。



▲このページのトップ ｜ NPO法人 natural science トップ

関連記事

ゼロから作るDeep Learning

【ニューラルネットワークの基礎研究31】ニューラルネットワークによる関数近似の検証（中間層１層の場合） 2018.08.02 【遠藤 理平｜ゼロから作るDeep Learning】

【ルンゲ・クッタで行こう！】水平自由単振子運動シミュレーション 2018.05.30 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】


【ニューラルネットワークの基礎研究30】任意の初期条件に対する運動を学習（重力＋空気抵抗力） 2018.05.26 【遠藤 理平｜ゼロから作るDeep Learning】

【ルンゲ・クッタで行こう！】単振子強制振動運動シミュレーション 2018.05.25 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】


【ニューラルネットワークの基礎研究29】放物運動の初期位置と初速度と経過時間から位置と速度を学習 2018.05.23 【遠藤 理平｜ゼロから作るDeep Learning】

【ニューラルネットワークの基礎研究28】放物運動の現在の位置と速度から未来の位置と速度を学習 2018.05.22 【遠藤 理平｜ゼロから作るDeep Learning】


【ニューラルネットワークの基礎研究27】放物運動の粘性抵抗係数と初速度と投射角度から飛距離を学習してみる 2018.05.10 【遠藤 理平｜ゼロから作るDeep Learning】

【ニューラルネットワークの基礎研究26】放物運動の軌跡から粘性抵抗係数と慣性抵抗係数を見積もる 2018.05.08 【遠藤 理平｜ゼロから作るDeep Learning】


【ニューラルネットワークの基礎研究25】放物運動の軌跡から空気抵抗係数を学習してみる 2018.05.07 【遠藤 理平｜ゼロから作るDeep Learning｜仮想物理実験室】

【ニューラルネットワークの基礎研究24】LASSO回帰因子を損失値に応じて小さくしてみる 2018.05.05 【遠藤 理平｜ゼロから作るDeep Learning】



▲このページのトップ ｜ NPO法人 natural science トップ




Warning: mysqli_connect(): (28000/1045): Access denied for user 'xsvx1015071_ri'@'sv102.xserver.jp' (using password: YES) in /home/xsvx1015071/include/natural-science/include_counter-d.php on line 8
MySQL DBとの接続に失敗しました