【ニューラルネットワークの基礎研究29】
放物運動の初期位置と初速度と経過時間から位置と速度を学習

「解析解は得られないが数値解が容易に得られる系で、学習の成果を簡単に検証できる問題」として、空気抵抗力が存在する放物運動を対象として物理的な運動を学習させています。
・ここまでの学習でできることをまとめると以下のとおりです。
（１）軌跡から粘性抵抗係数を見積もることができる。
（２）その粘性抵抗係数を用いて初速度と投射角度を与えるとその飛距離がわかる。
→ その結果、最大飛距離となる初速度に対する投射角度を予測できる。
（３）粘性係数と現時点での位置と速度からその後の位置と速度がわかる

本稿では視点を変えて、粘性係数と初期位置と初期速度と経過時間をからその後の位置と速度を学習させてみます。

ニューラルネットワークの基本パラメータ

・ニューラルネットワークの構造：順伝播型ニューラルネットワーク（FFNN）
・学習方法：通常の勾配法（学習率固定、逆誤差伝搬法）
・学習率：eta = 0.01;
・ミニバッチ数：100 （サンプルは無限に用意できるためミニバッチという概念は存在しませんが、ランダムに用意したミニバッチ数分のサンプルに対する平均を用いて学習を進める）
・活性化関数（中間層）：ReLU（ランプ関数）
・活性化関数（出力層）：恒等関数
・損失関数：２乗和
※独立したネットワークを１０個用意してそれぞれ個別に学習させて、学習効果の高かった上位５つの「学習回数」vs「損失値」をグラフ化します。

中間層２層のニューラルネットワーク（6-500-500-4）

初速度、投射角度、粘性抵抗係数を毎回ランダムに与えて、１秒間の軌跡を0.01秒刻みで学習させた結果です。

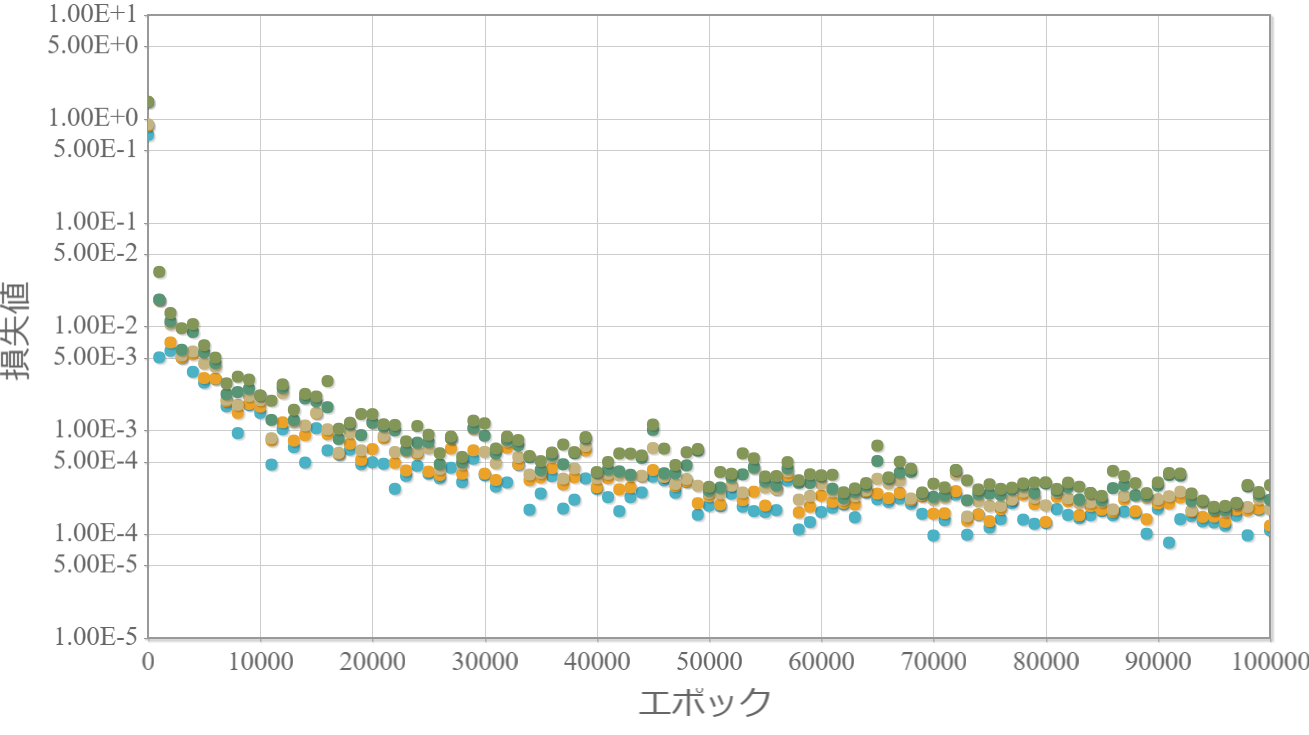
（追記）初速度、投射角度、粘性抵抗係数を毎回ランダムに与えて、３秒間の軌跡を0.01秒刻みで学習させた結果です。

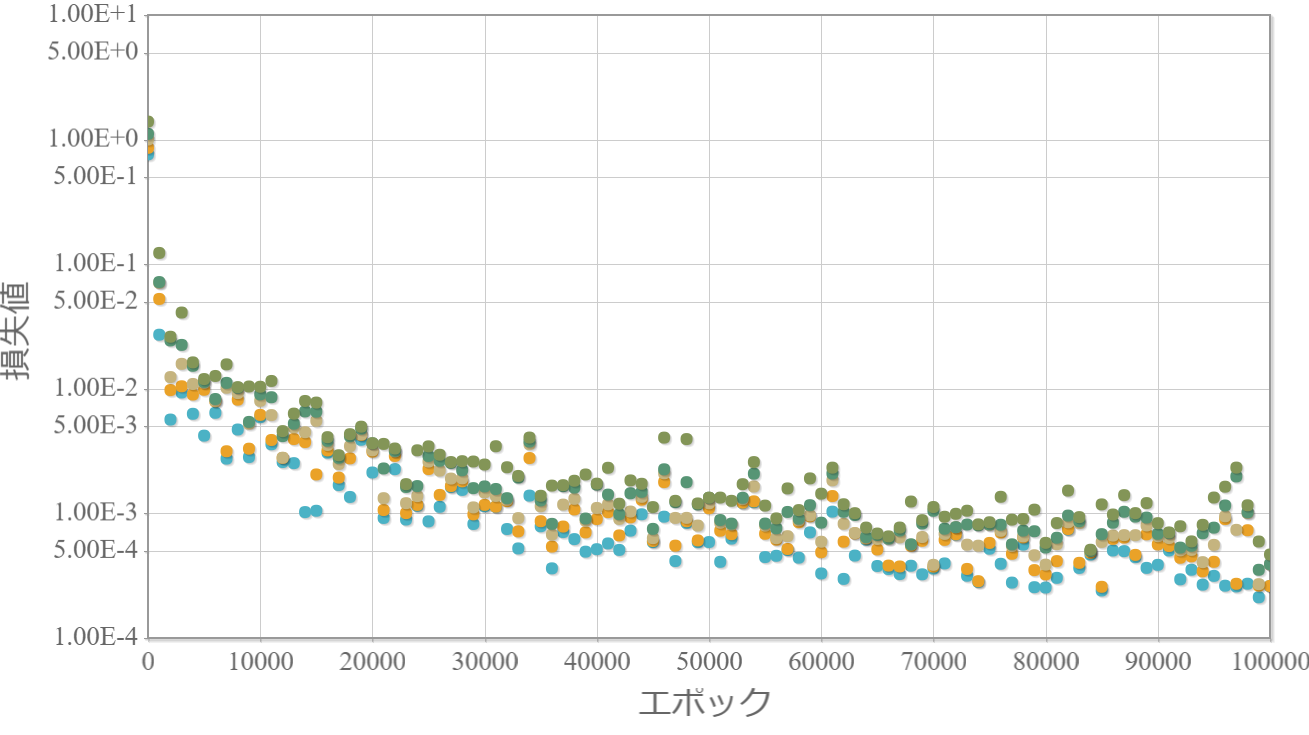
100,000回学習後のチェック

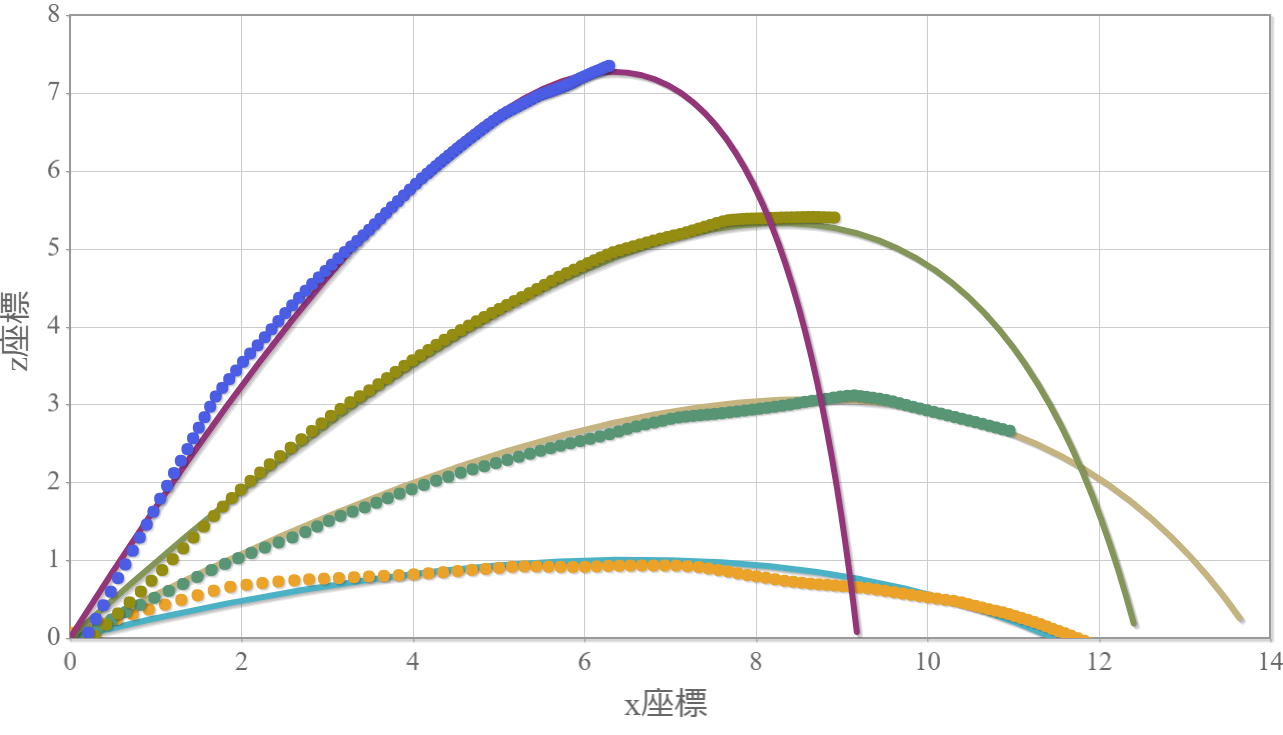
初速度20、粘性抵抗係数を1.0として、投射角度を１５°、３０°、４５°、６０°、７５°の軌跡の数値計算結果（実線）と、ネットワークで計算した１秒間の軌跡（黒丸）を重ねて描画しています。概ね数値解の上に乗っていることが確認できます。

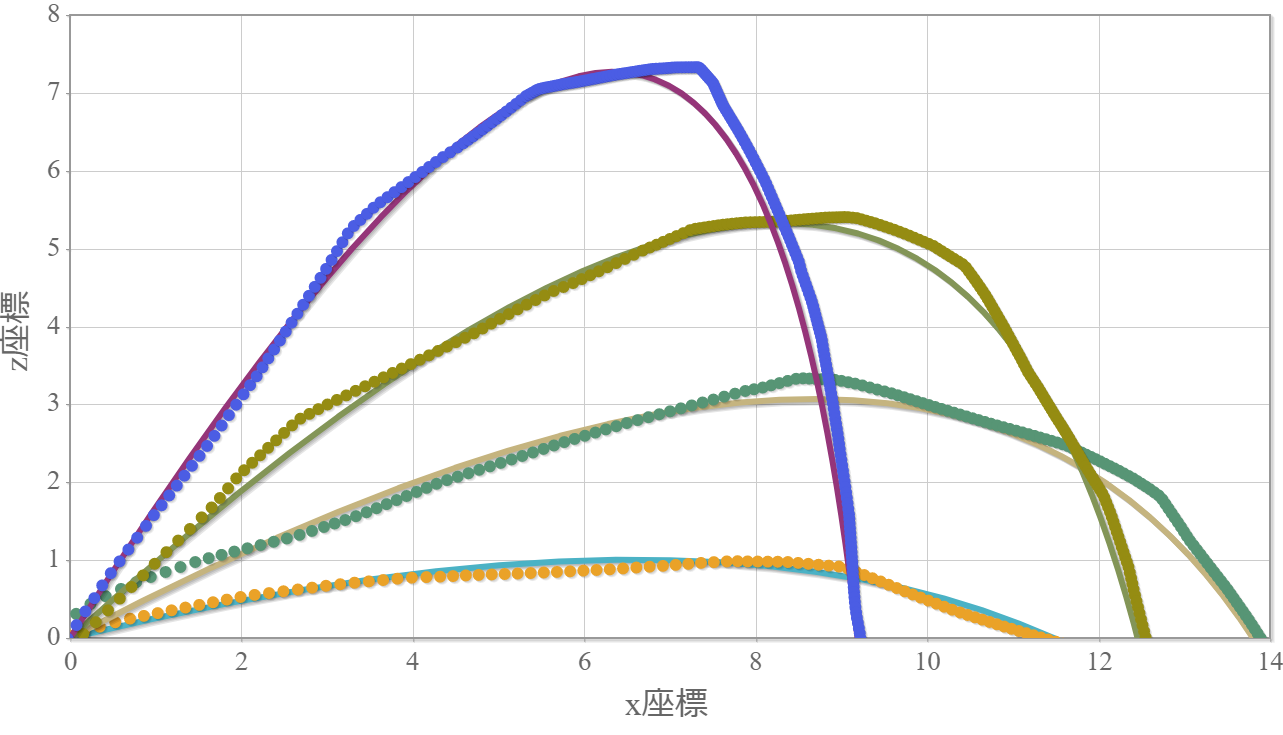
（追記）上記と同じ条件で３秒間の軌跡を学習させた場合の結果です。

考察と次の課題

・学習方法で一つ失敗だったのが、初期状態の学習（時刻t=0）を怠ったため、原点での誤差が大きくなってしまった。
→ 次回は初期状態も学習させる
・この方法が良いのは、「粘性抵抗係数と初速度と投射角度から飛距離を学習」する場合は１回の投射で１個のデータしか得られないが、軌跡をまるごと学習対象とすることでデータ数が時間刻み数個分取得できる。
・さらに、入力データを「投射角度」ではなく「初期速度」とすることで放物運動の一般的な状態を初期状態として扱うことができる。
→ つまり、投射運動以外にもそのまま適用できる。自分がやりたい方向に少し近づいた気持ち。
（追記）学習対象が１秒間から３秒間と伸ばすと学習は難しくなることがわかる。

・投射運動に限らずどんな初期条件でも１秒間の軌跡を追随する学習を行ってみる。
→これができれば、次の１秒後の軌跡もつなげていくことで予測できる

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/FFNNs_epoch_ProjectileMotion_AirResistance4.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。