HOME > natural science Laboratory > コンピュータ・シミュレーション講座 > 仮想物理実験室

【量子力学再入門14】
複素ポテンシャルによる吸収と放出

文責：遠藤 理平 （2018年5月24日） カテゴリ：仮想物理実験室(325)

スペクトル法による数値計算は少し置いておいて、シュレディンガー方程式のポテンシャル項が複素数の場合の一般解を調べてみます。 通常、シュレディンガー方程式のポテンシャル項はハミルトニアンがエルミートである必要性から実数を取る必要があります。しかしながら、光学系における複素屈折率とのアナロジーで、複素数のポテンシャル項を導入することで吸収・放出を現象論的に表現することができます。本稿では、ポテンシャル項に複素数が含まれる場合の一般論を議論し、吸収・放出層が存在する系における単一平面波の様子を調べます。

空間一様な媒質中の平面波

複素ポテンシャルが空間的に均一な場合の平面波の表式と分散関係を導出します。シュレディンガー方程式におけるポテンシャルVとエネルギーE、波数kを実部と虚部に分けて、それぞれが満たす関係式を示します。

V=V_{\rm r} +iV_{\rm i}, E=E_{\rm r} +iE_{\rm i}
k=k_{\rm r} +ik_{\rm i}, \omega = \omega_{\rm r} +i\omega_{\rm i}

ただし、V_{\rm r}, V_{\rm i}, E_{\rm r}, E_{\rm i}, k_{\rm r}, k_{\rm i}, \omega_{\rm r}, \omega_{\rm i}はすべて実数とします。平面波の解

\varphi(x,t)=e^{ikx -i\omega t} = e^{ (ik_{\rm r}-k_{\rm i})x + (\omega_{\rm i}-i\omega_{\rm r} )t }

をシュレディンガー方程式に代入して整理すると

\frac{\hbar^2(k_{\rm r}+ik_{\rm i})^2}{2m} +V_{\rm r} + iV_{\rm i} = E_{\rm r} +iE_{\rm i}
E_{\rm r} +iE_{\rm i} =\hbar(\omega_{\rm r} +i\omega_{\rm i})

となり、実数部と虚数部を比較すると次の連立方程式が得られます。

\frac{\hbar^2(k_{\rm r}^2-k_{\rm i}^2)}{2m} +V_{\rm r} =E_{\rm r}
\frac{\hbar ^2k_{\rm r}k_{\rm i}}{m} + V_{\rm i} = E_{\rm i}
E_{\rm r} =\hbar\omega_{\rm r}
E_{\rm i} =\hbar\omega_{\rm i}

EとVは与えられているとして、波数の実部と虚部を求めてみましょう。 k_{\rm i} を消去すると、４次方程式

k_{\rm r}^4-\frac{ 2m(E_{\rm r} - V_{\rm r} )}{ \hbar^2 }k_{\rm r}^2 -\frac{ m^2(E_{\rm i} - V_{\rm i} )^2}{ \hbar^4 } =0

が得られ、２次方程式の解の公式から

k_{\rm r}^2= \frac{ m}{ \hbar^2 } \left[ E_{\rm r} - V_{\rm r} \pm\sqrt{(E_{\rm r} - V_{\rm r} )^2+(E_{\rm i} - V_{\rm i} )^2} \right]

となります。k_{\rm r}は実数なのでk_{\rm r}^2 \geq 0から第二項目の符号は正のみが解に対応し、全体の平方根を取ることでk_{\rm r}が得られます。そして直ちにk_{\rm i}も得られます。

k_{\rm r}= \pm\frac{ \sqrt{m}}{ \hbar } \sqrt{ E_{\rm r} - V_{\rm r} + \sqrt{(E_{\rm r} - V_{\rm r} )^2+(E_{\rm i} - V_{\rm i} )^2} }
k_{\rm i}= \frac{ \pm\sqrt{m}(E_{\rm i} - V_{\rm i} )}{ \hbar\sqrt{ E_{\rm r} - V_{\rm r} + \sqrt{(E_{\rm r} - V_{\rm r} )^2+(E_{\rm i} - V_{\rm i} )^2} } }

ポテンシャルに複素数が存在する均一媒質中では、どのようなV_{\rm i}と E_{\rm i}を与えても波動関数の指数部に実数が現れてしまい、xの方端ないしtの方端で発散してしまうため、定常状態は存在しえないことがわかりました。


吸収・放出層が存在する系


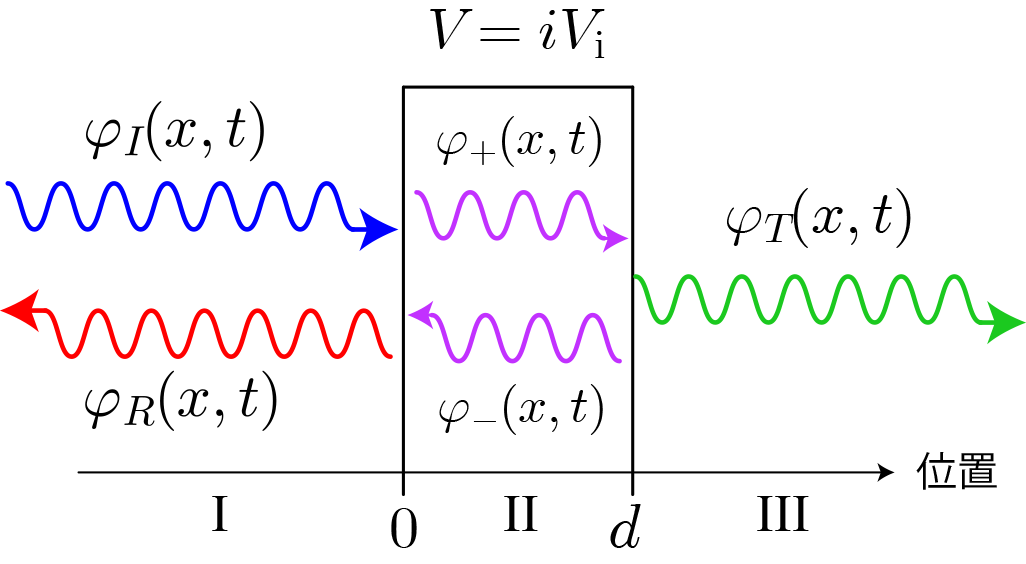
上図のような自由空間に吸収・放出層が１層ある場合を考えます。自由空間におけるエネルギーE、振動数\omegaは実数なので、境界面における接続条件から吸収・放出層のEと\omegaも必ず実数となる必要があります。そのため、 E_{\rm i}=0 、\omega_{\rm i} =0から吸収・放出層（II）の波数の実部と虚部は次のとおりになります。

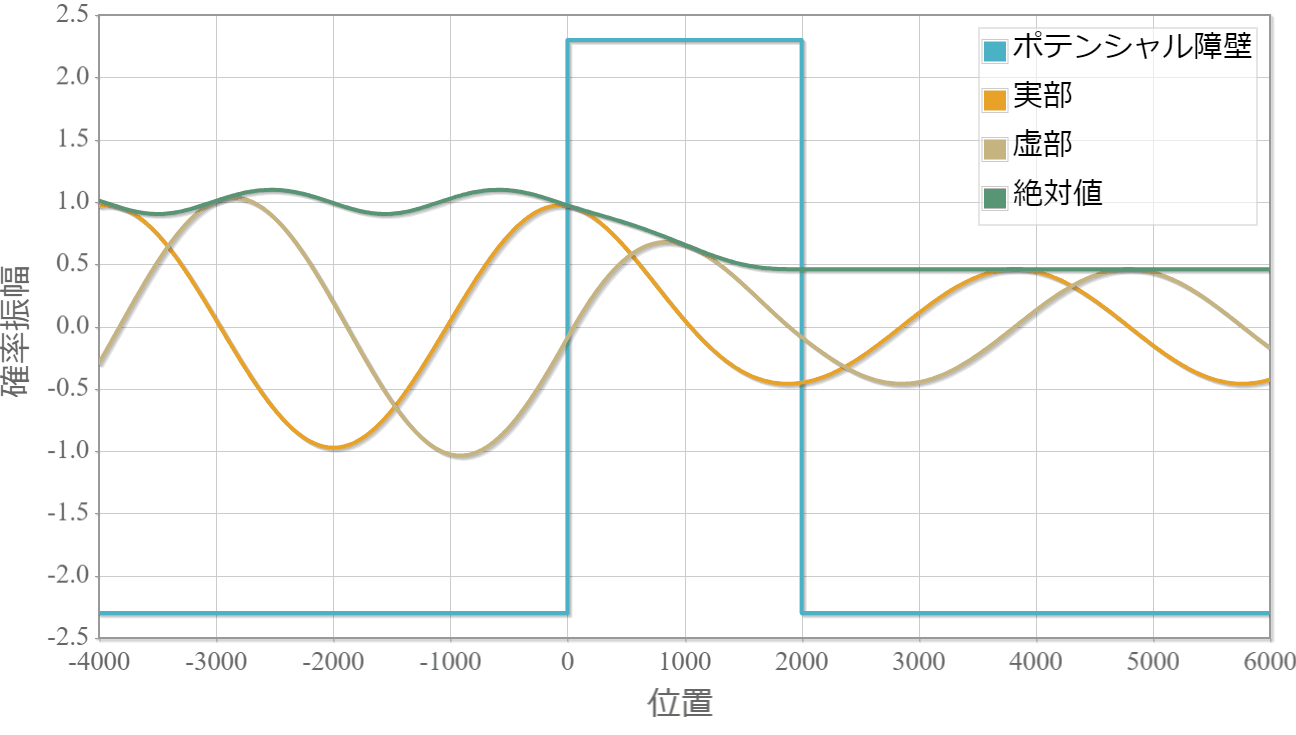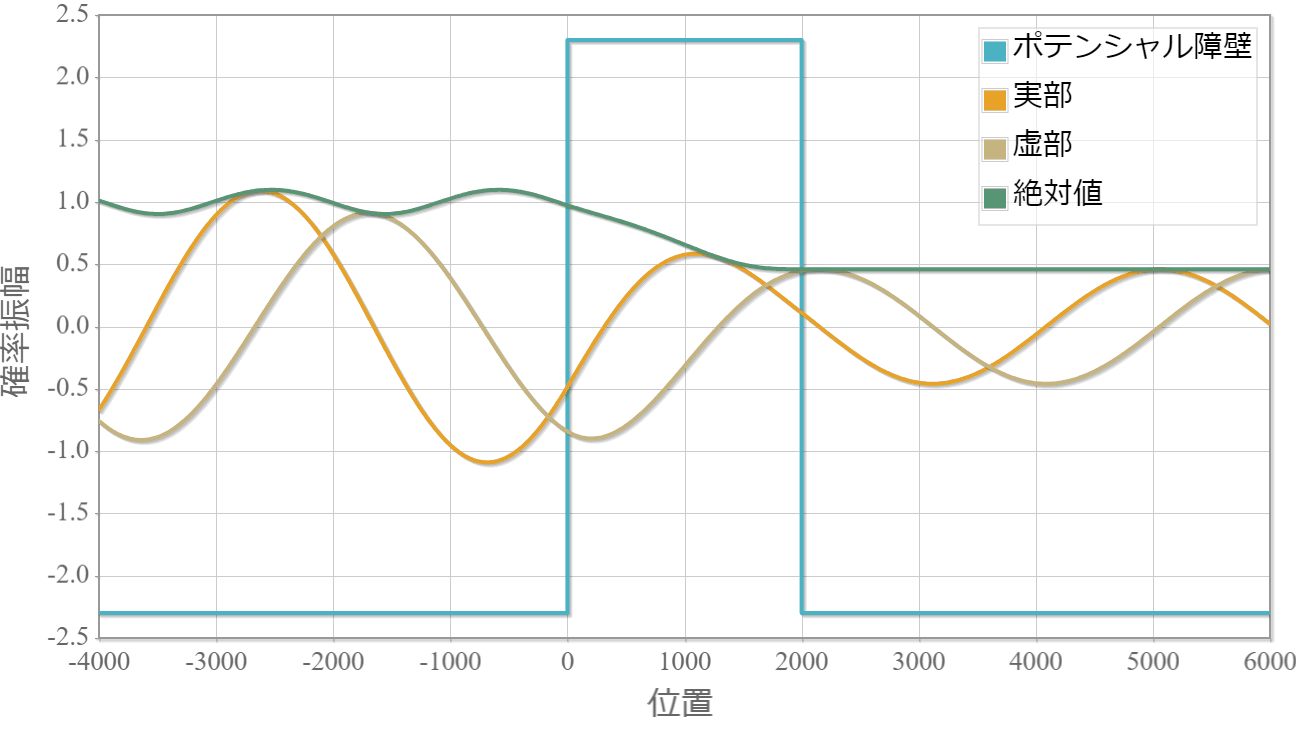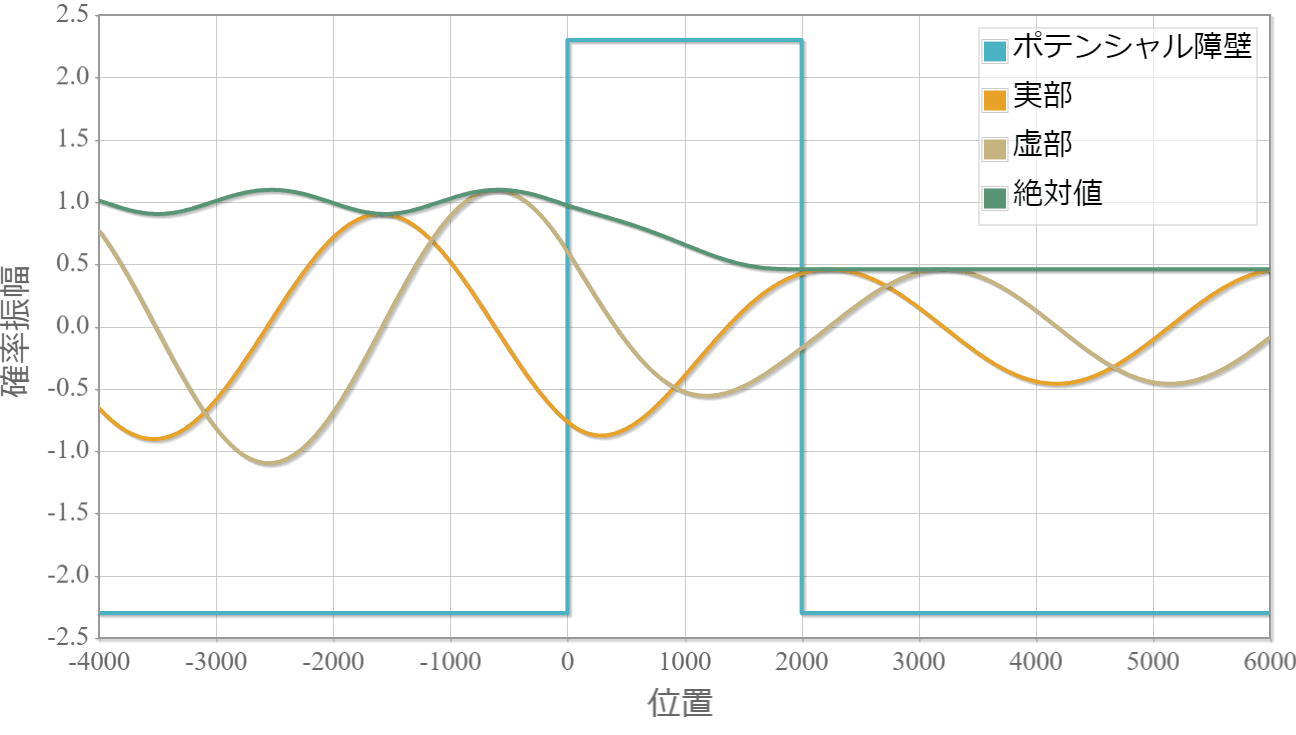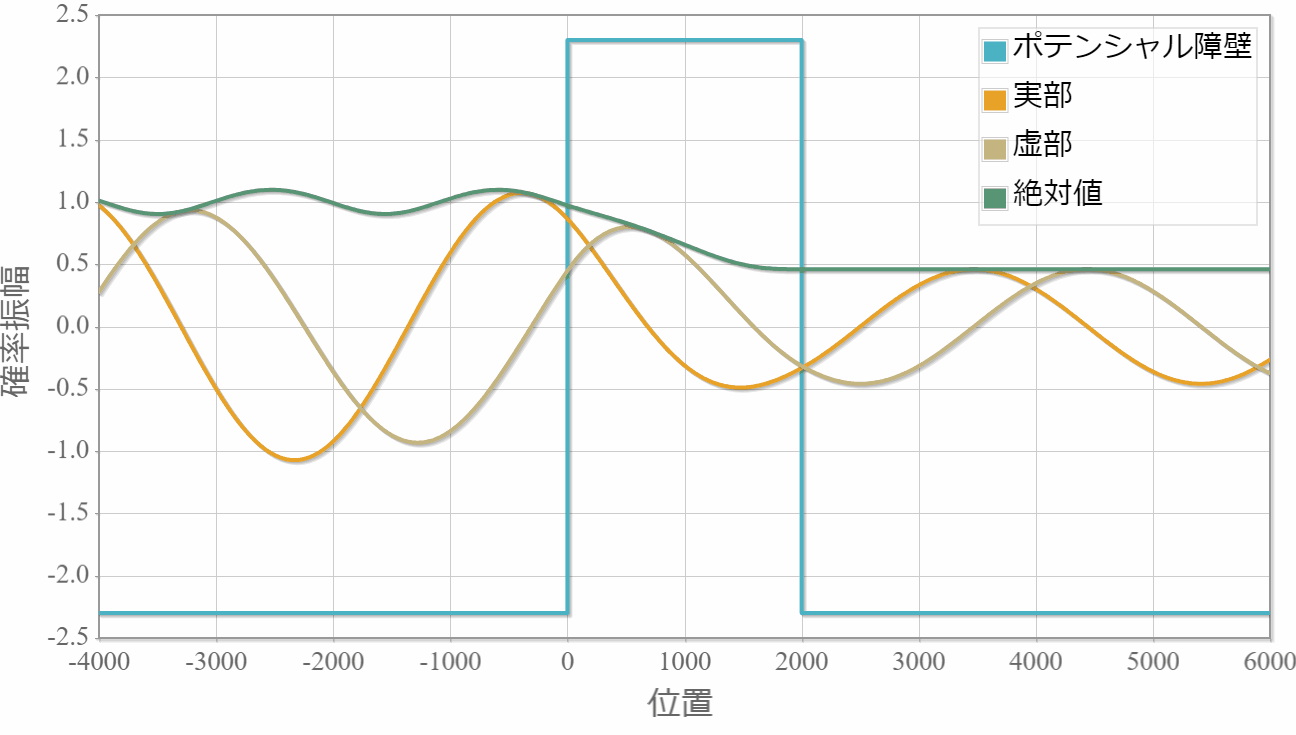
k_{\rm IIr}= \pm\frac{ \sqrt{m}}{ \hbar } \sqrt{ E - V_{\rm r} + \sqrt{(E - V_{\rm r} )^2+V_{\rm i} ^2} }
k_{\rm IIi}= \frac{ \mp\sqrt{m}\, V_{\rm i} }{ \hbar\sqrt{ E - V_{\rm r} + \sqrt{(E - V_{\rm r} )^2+V_{\rm i}^2} } }

後はこの波数を転送行列に適用することで自由空間に吸収・放出層が１層ある系の平面波の運動を調べることができます。 次の図は10eVのエネルギーの平面波を複素ポテンシャルへ入射した際の運動です。複素ポテンシャルの複素数値の正負が放出と吸収にそれぞれ対応する様子がわかります。

V=5.0i[\rm eV]


V=-5.0i[\rm eV]


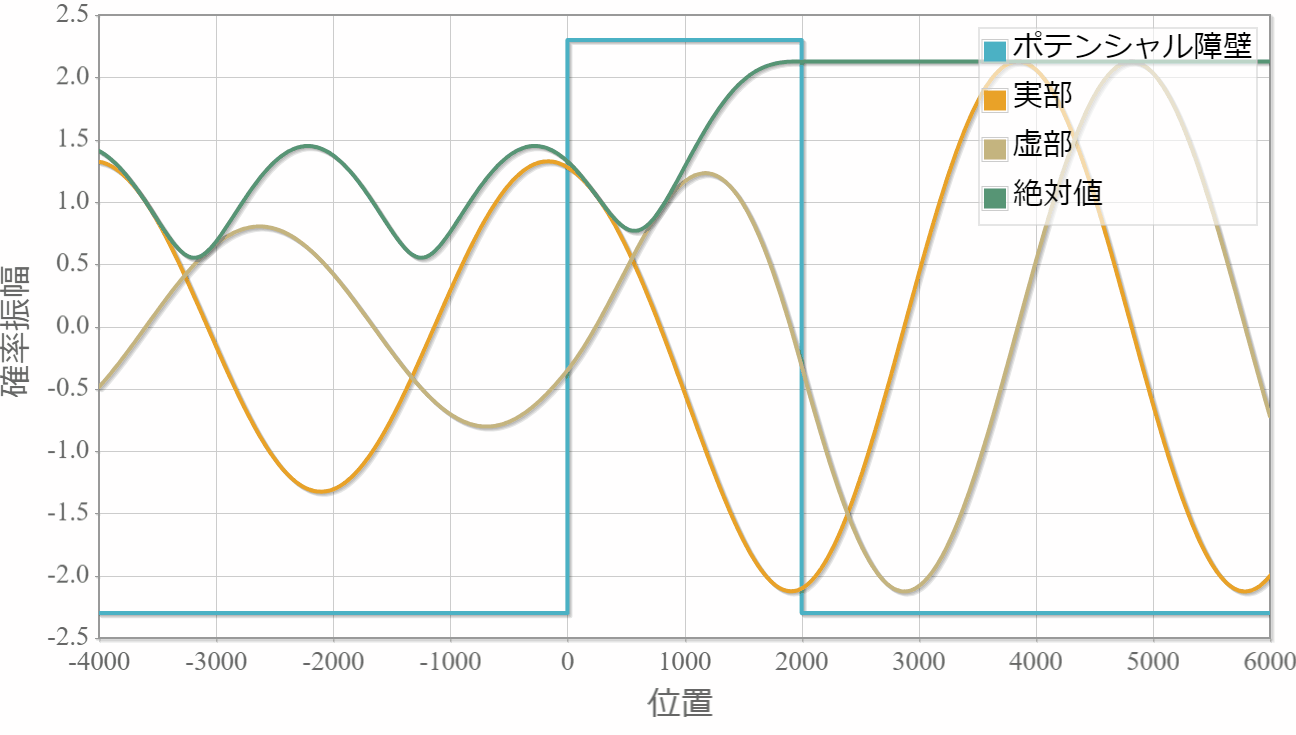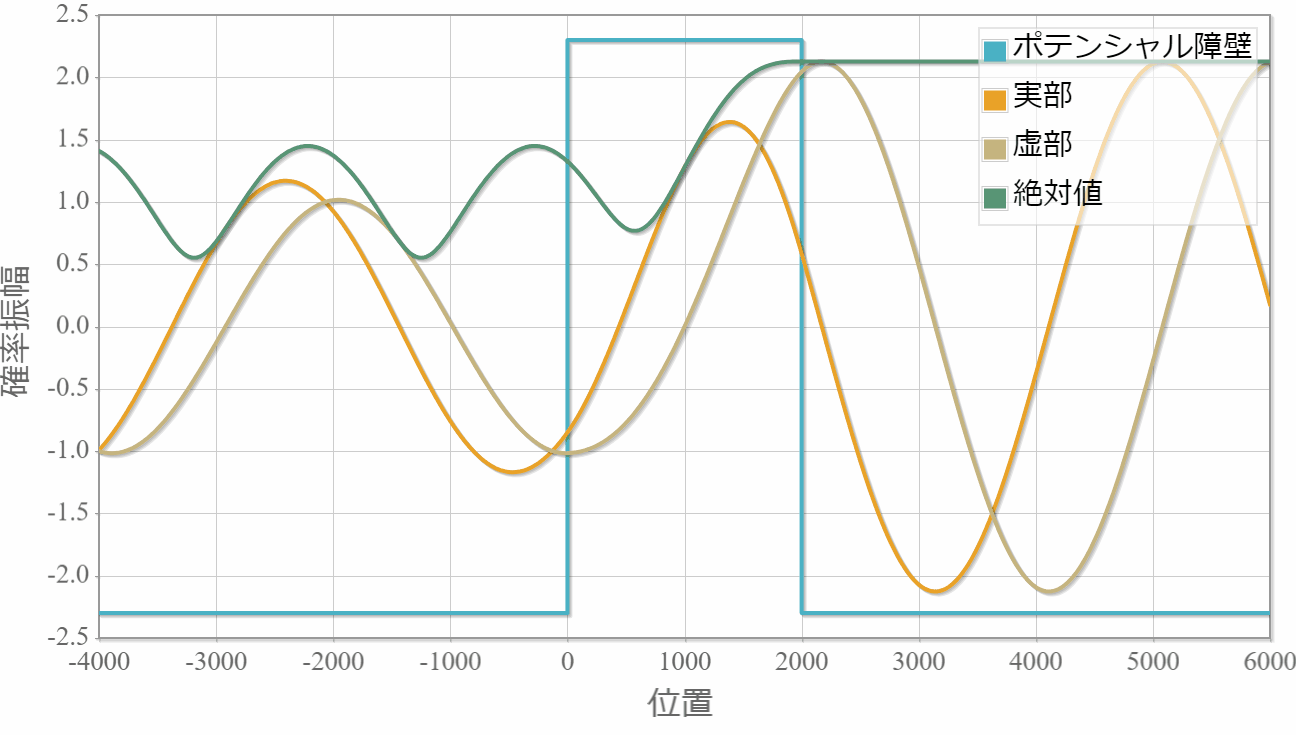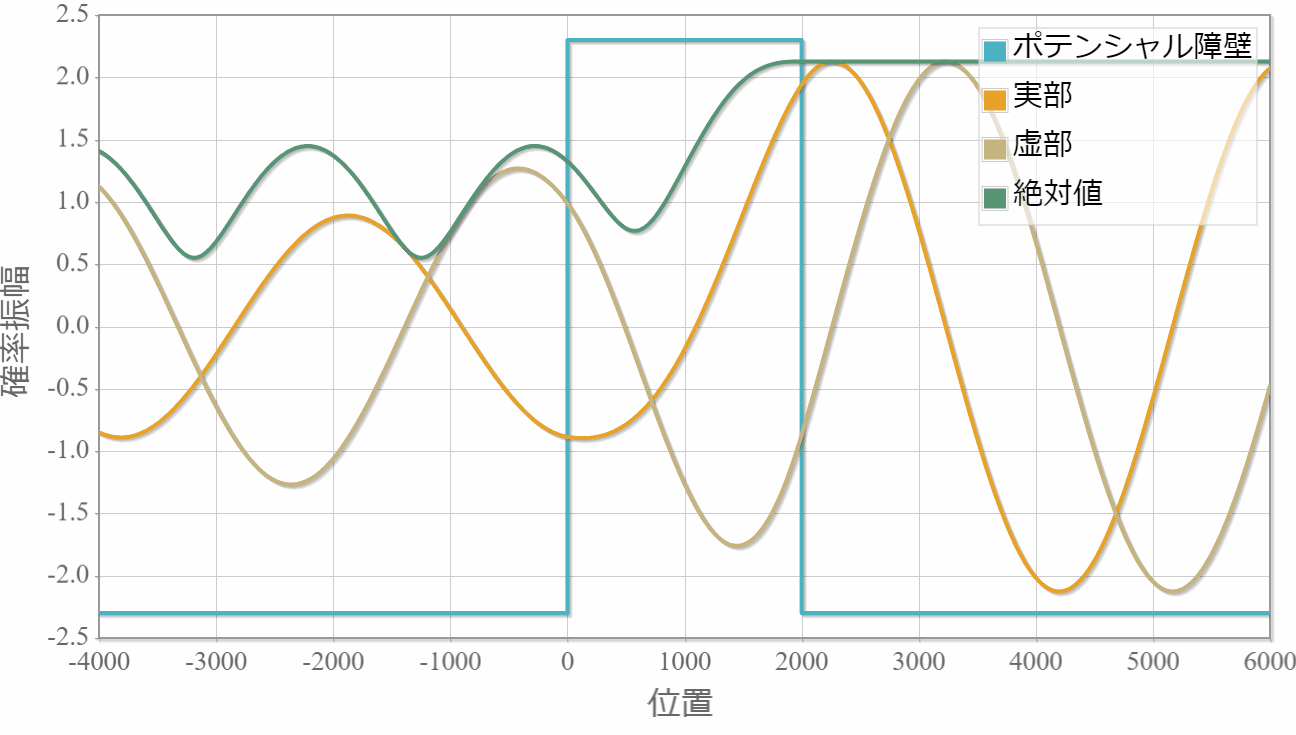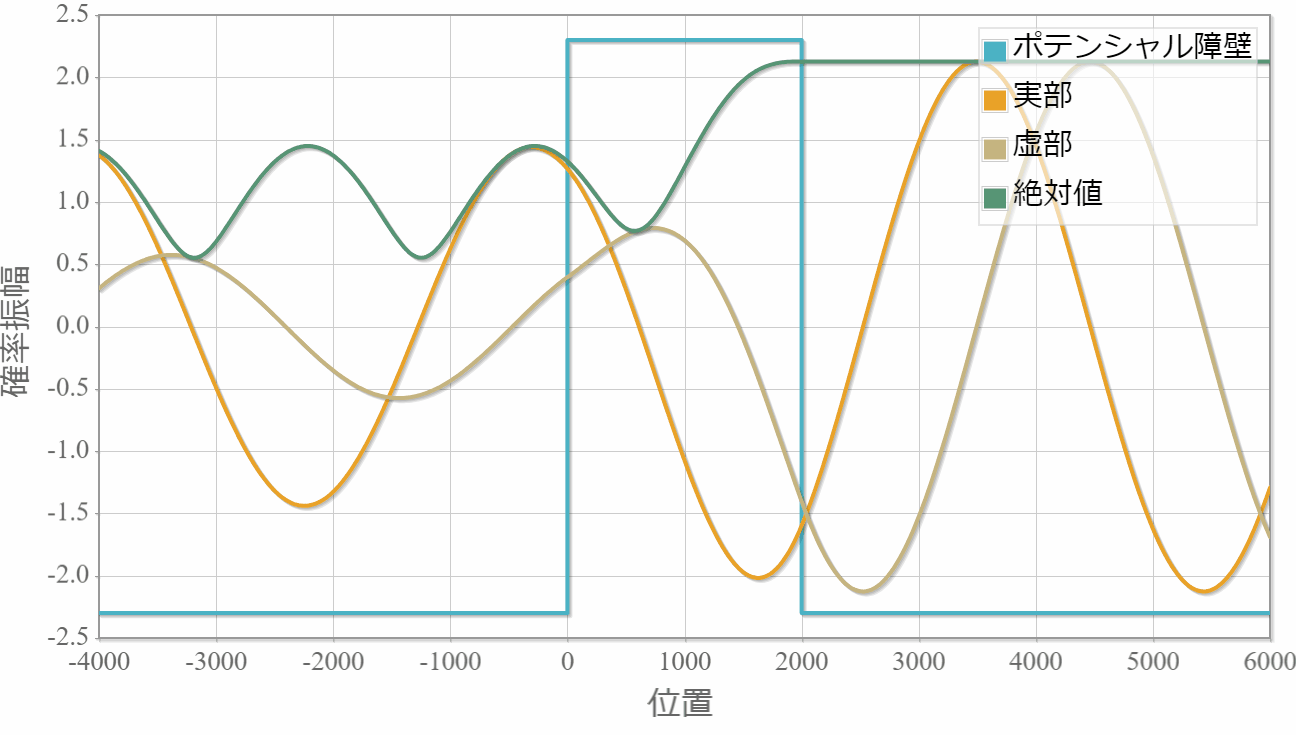
プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics14.cpp
※VisualC++、GCC（MinGW）で動作確認しています。



▲このページのトップ ｜ NPO法人 natural science トップ

関連記事

仮想物理実験室

【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤 理平｜仮想物理実験室】

【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤 理平｜仮想物理実験室】


【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤 理平｜仮想物理実験室】

【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤 理平｜仮想物理実験室】


【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤 理平｜仮想物理実験室】

【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤 理平｜仮想物理実験室】


【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤 理平｜仮想物理実験室】

【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤 理平｜仮想物理実験室】


１０日で作る量子ドットコンピュータ～動作原理を数値シミュレーション！～【５日目】１量子ビット万能量子ゲートを設計しよう！ 2019.09.06 【遠藤 理平｜仮想物理実験室】

１０日で作る量子ドットコンピュータ～動作原理を数値シミュレーション！～【４日目】量子井戸の電子状態の基礎実験３：２重量子井戸で量子ビットを改良！ 2019.08.27 【遠藤 理平｜仮想物理実験室】



▲このページのトップ ｜ NPO法人 natural science トップ




Warning: mysqli_connect(): (28000/1045): Access denied for user 'xsvx1015071_ri'@'sv102.xserver.jp' (using password: YES) in /home/xsvx1015071/include/natural-science/include_counter-d.php on line 8
MySQL DBとの接続に失敗しました