【機械学習基礎研究1】
強制振動運動の最適化学習の準備

単振子運動とは伸び縮しないひもに結び付けられたおもり（単振り子）が重力中で振動する運動です。単振り子の強制振動運動とはひもの反対側の支点を振動させることで、振り子を強制的に振動させる運動を指します。単振り子の周期は振幅（振動の大きさ）によって異なるため、振り子がよく触れる支点の振動数（共鳴振動数）も振幅によって異なります。つまり、単一の振動数だけで強制振動させてもある程度以上の振幅は得られません。そこで、振り子が最もよく触れる支点の振動の与え方を機械学習で学習させることを考えます。本稿ではその一つ前に、機械学習との比較検証用として物理的な方法論で振動の与え方を考えてみます。

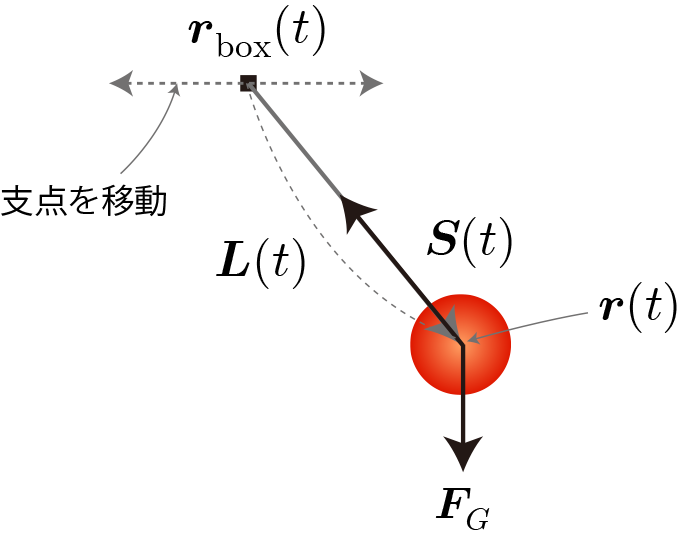
支点の振動方向（水平）をx軸方向、上方をz軸方向とします。支点の振動の時間依存性を次式のように角振動数に分解します。

\begin{align} \boldsymbol{r}_{\rm box}(t) = l \sum_{n} b_n\sin(\omega_n t)\, \hat{\boldsymbol{e}}_x \end{align}

これは支点の振動運動の時間依存性に対するフーリエ級数展開に対応しています。$l$は振動の振幅の大きさ、$b_n$はフーリエ級数の展開係数、$\omega_n$ は角振動数で$\omega_n = 2\pi n/T $、$T$はフーリエ級数展開の周期です。フーリエ級数の項数が大きいほど細かな運動を表現できます。今回の条件はひもの長さ$L = 1$、支点の振幅$l=0.2$、フーリエ級数の周期と項数はそれぞれ$T=100$、$N=100$とします。また、展開係数には$\sum_n |b_n|=1$の条件を課すことにします。ちなみに強制振動運動シミュレーションに必要な支点の速度ベクトルと加速度べクルはそれぞれ次のとおりです。

\begin{align} \boldsymbol{v}_{\rm box}(t) &= l \sum_{n} b_n\omega_n\cos(\omega_n t)\, \hat{\boldsymbol{e}}_x\\ \boldsymbol{a}_{\rm box}(t) &=-l \sum_{n} b_n\omega_n^2\sin(\omega_n t)\, \hat{\boldsymbol{e}}_x \end{align}

制限時間内（30秒）で振り子の力学的エネルギーが最大となるb_nの分布を導くことを目的とします。

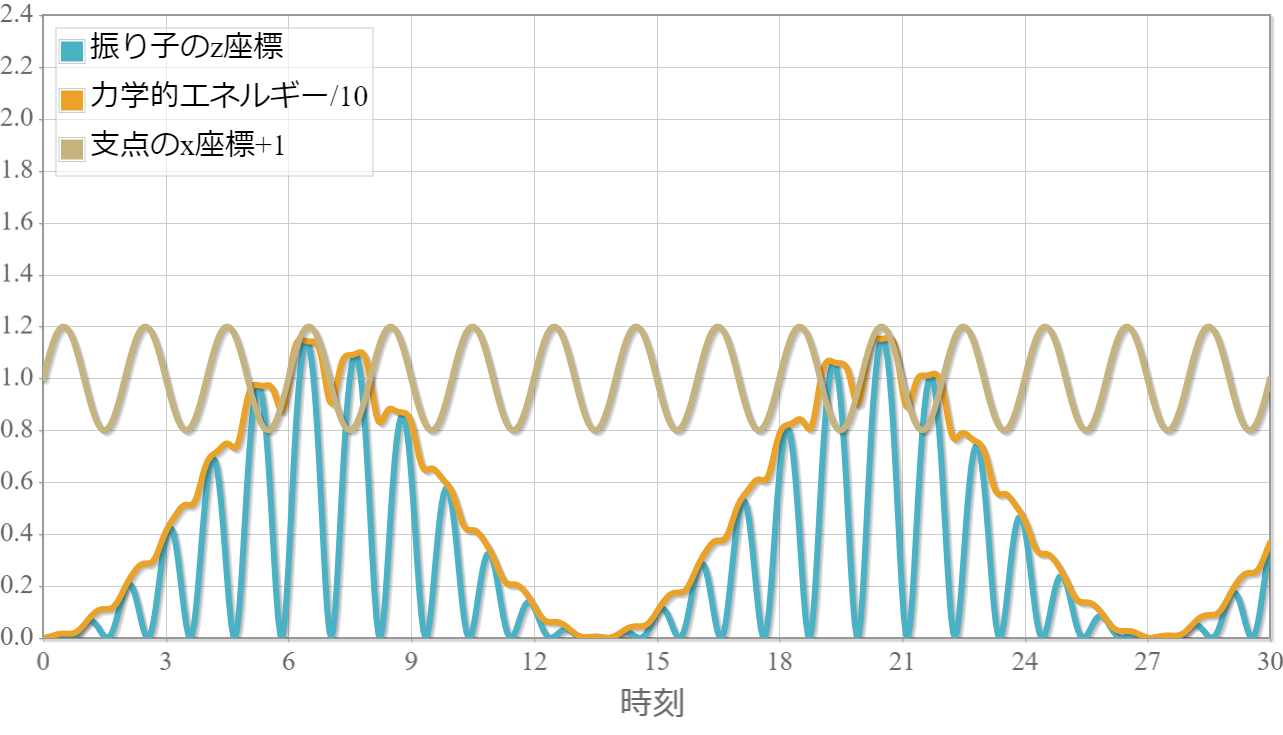
比較対象：静止時の共鳴角振動数を与えた場合

下図は静止時の共鳴角振動数 $\omega = \sqrt{g/L} \simeq 3.162 $（$g=10$として計算）に一番近い展開係数$b_{50}=1$（それ以外０）を与えた場合の振り子の運動の様子です（横軸は時刻）。青線はおもりのz座標、橙線は力学的エネルギーを１０で割った値、茶線は支点のx座標です（$x=1$を中心にプロットしています）。ひもの長さが１なので、おもりのz座標が1で振り子が水平、おもりのz座標が2で振り子が真上を意味します。重力加速度を$g=10$としているため、「力学的エネルギー/10 - おもりのz座標」が運動の大きさを表します。静止時の共鳴角振動数を与えた場合、だいたい振り子は水平程度まで触れた後にもとに戻るという運動となることを表しています。

共鳴角振動数を与えた際の強制振動運動の様子

$b_n$の導出方法

力学的エネルギー$E$を時刻$t$と展開係数$b_n$の関数$ E(t,{b_1,b_2,\cdots,b_N}) $と考えます。単純な$b_n$の更新方法は

\begin{align} b_n\leftarrow b_n+\eta \,\frac {\partial E(t,b_1,b_2,\cdots ,b_N)}{\partial b_n} \end{align}

ですが、これだけでは$\sum_n |b_n|=1$の条件が考慮されないため、一方的に大きな値へ発散していきます。そこで、１つの展開係数を上記の式で更新後、$\sum_n |b_n|=1$となるように全部の展開係数を規格化します。そして規格化後の展開係数を用いて$E$を計算後、元の$E$よりも大きければ「採用」とします。この操作をすべての展開係数に対して実行して、b_nを更新していきます。そして、すべての展開係数を更新後に規格化を行います。この方法の場合、最後にまた規格化を行うために、実際に$E$が大きくなるかはやってみなければわかりませんが、まずは試してみます。ちなみに、このようなまどろっこしい操作が必要な理由は、$\sum_n |b_n|=1$を拘束条件として与えながらの偏微分が簡単には計算できないことに起因します。もし、自動的に拘束条件を満たすようにするには、統計力学で用いるようなラグランジュ未定乗数法を用いて力学的エネルギーの自由度を増やした自由エネルギーの最大化を考える必要があります。

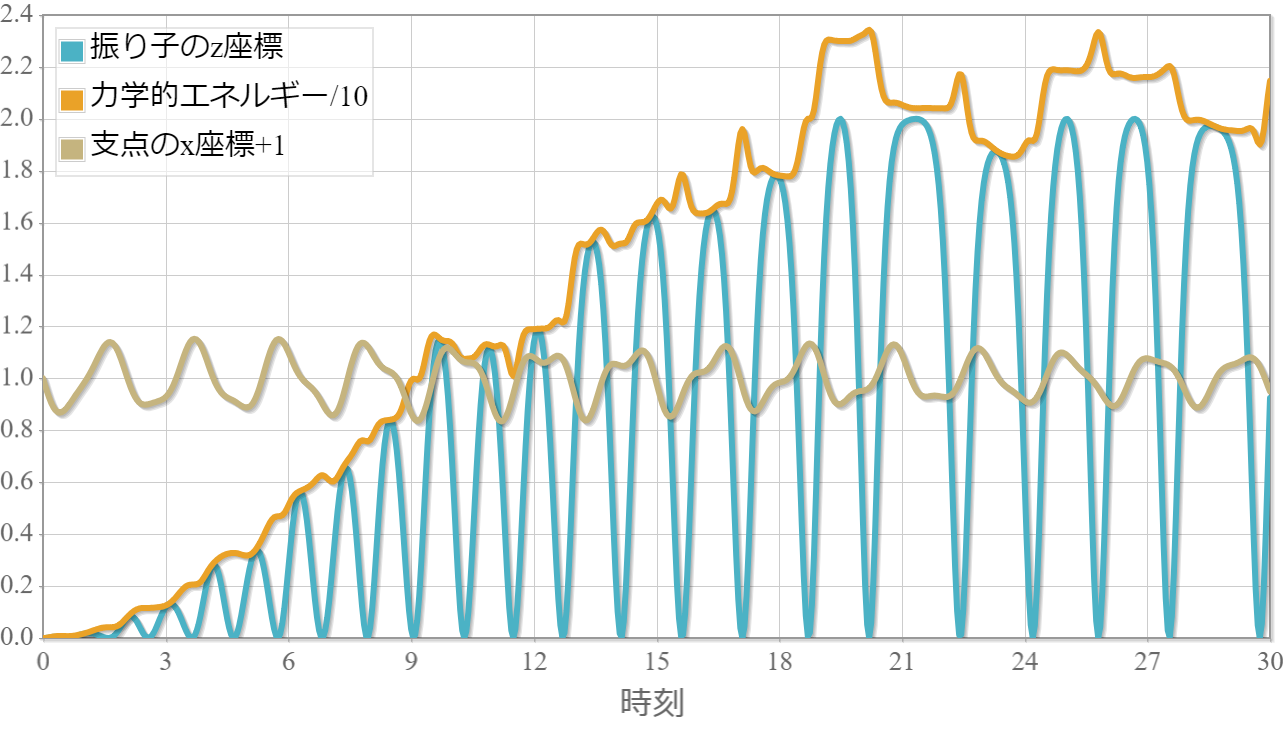
強制単振子の力学的エネルギーが最大となった運動

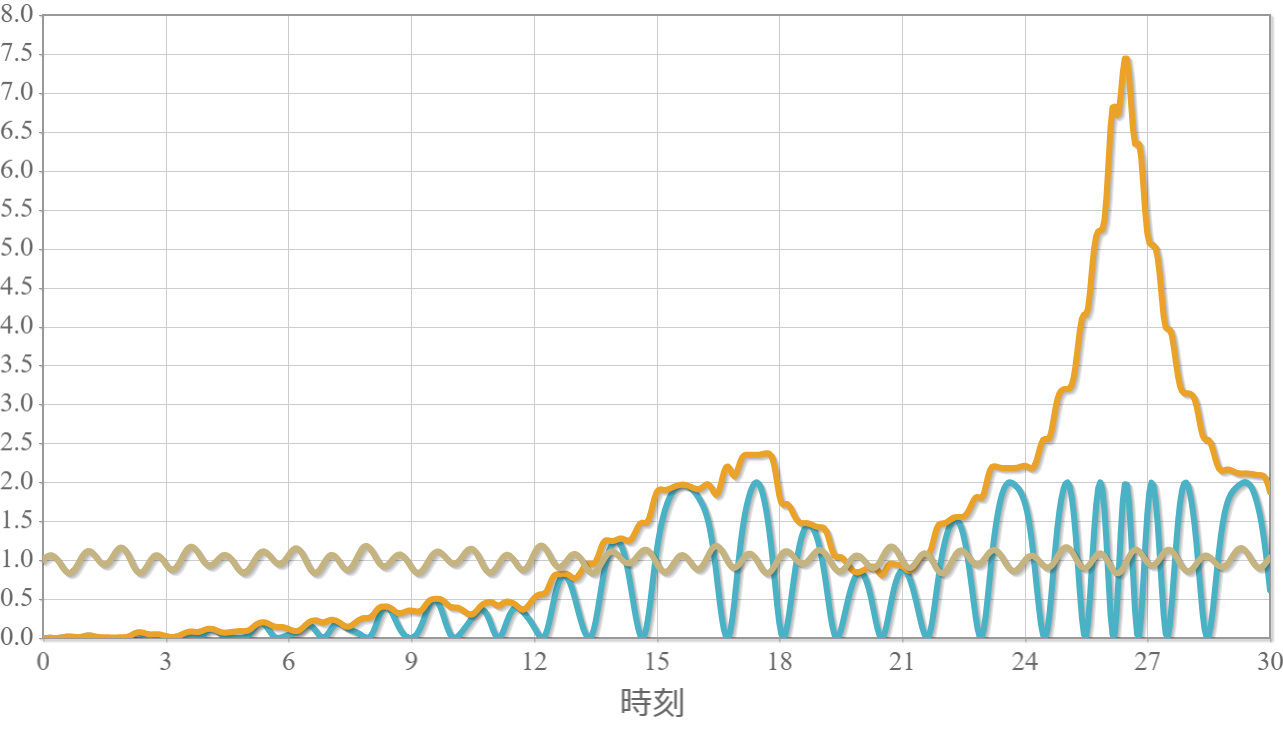
次の図は強制単振子の力学的エネルギーが最大となった運動の様子です。19.5秒後あたりで振り子が回転している様子が確認できます。

強制単振子の力学的エネルギーが最大となった運動

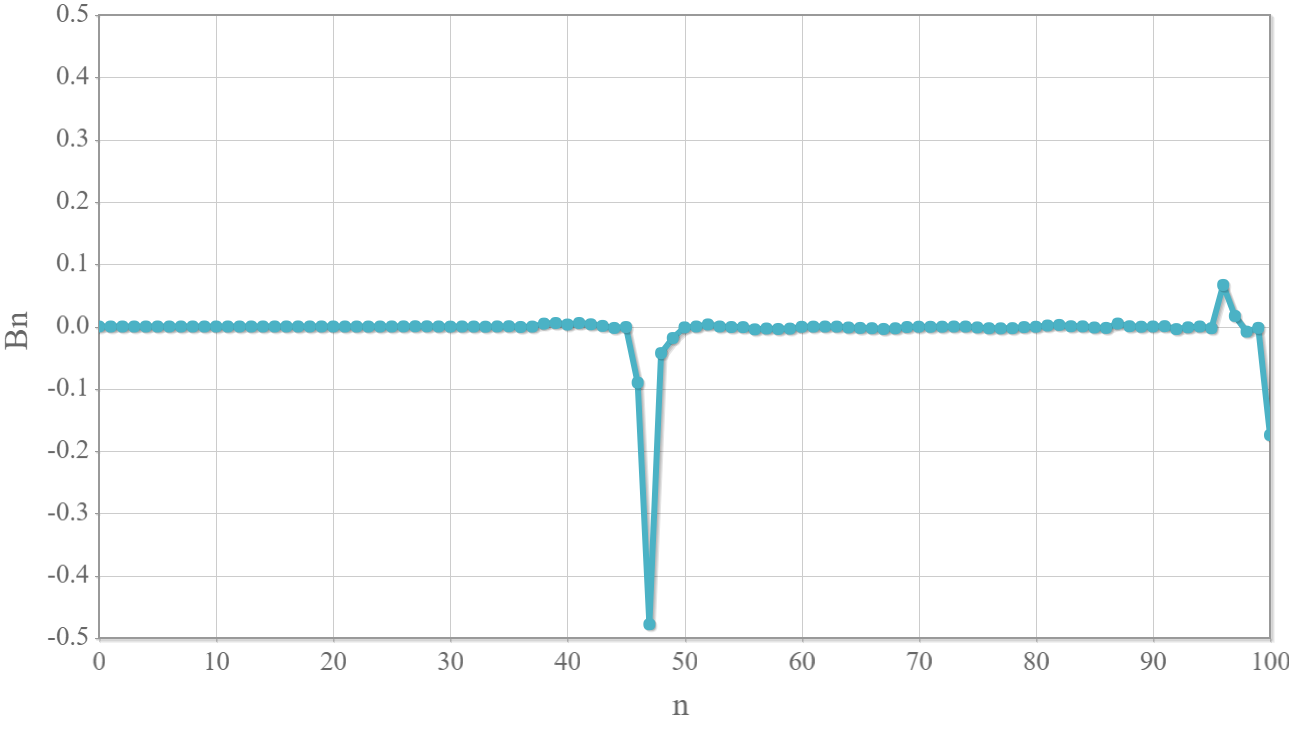
下図はこのときの展開係数の分布です。$n=47$、$n=96$、$n=100$を中心としたピークがあり、それ以外はほぼ０となっている様子がわかります。$n=47$は静止時の共鳴角振動数近傍、$n=96, 100$は大きな振動数を表しています。今回の計算で気がついたことですが、展開係数の項数を100個としたことは適切ではなく、もっと高振動数成分も必要なので展開係数の個数を増やす必要があることがわかりました。

展開係数の値

とりあえずこれを比較対象として、次回は機械学習に取り組みます。

（追記）フーリエ級数の項数を２００まで増やした結果

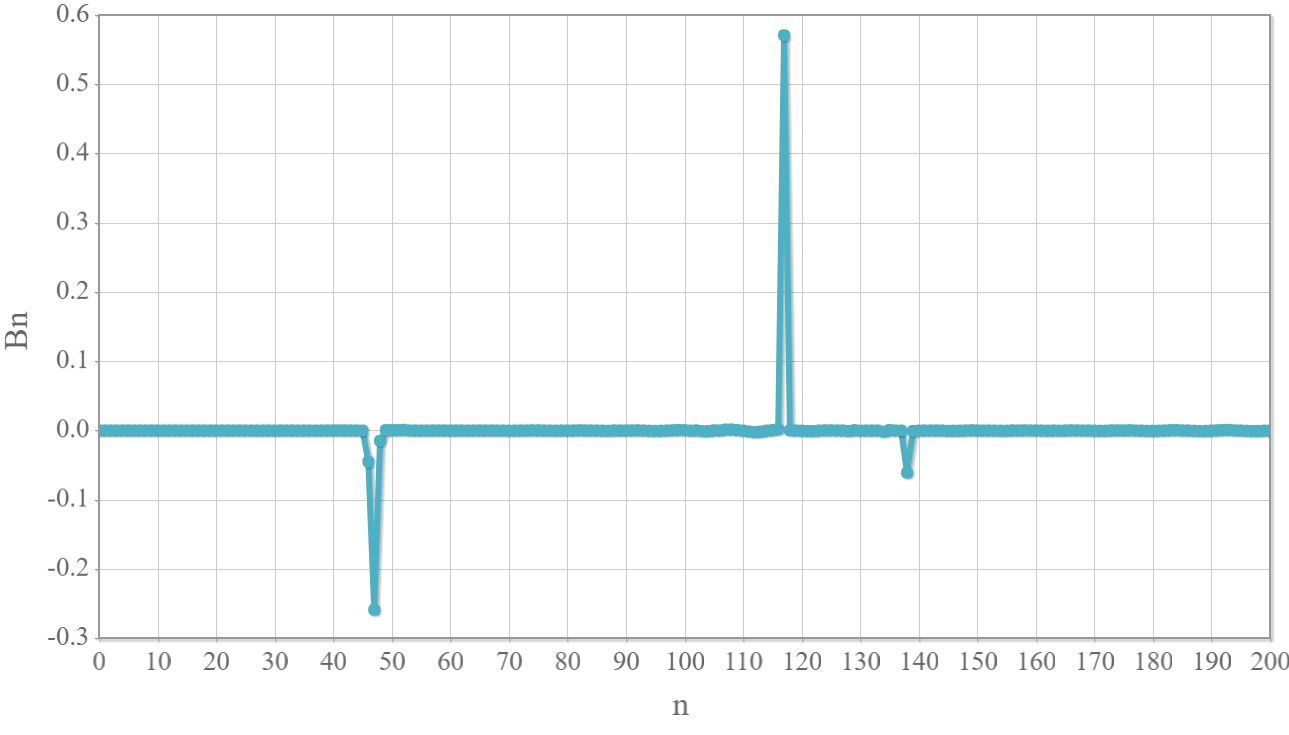
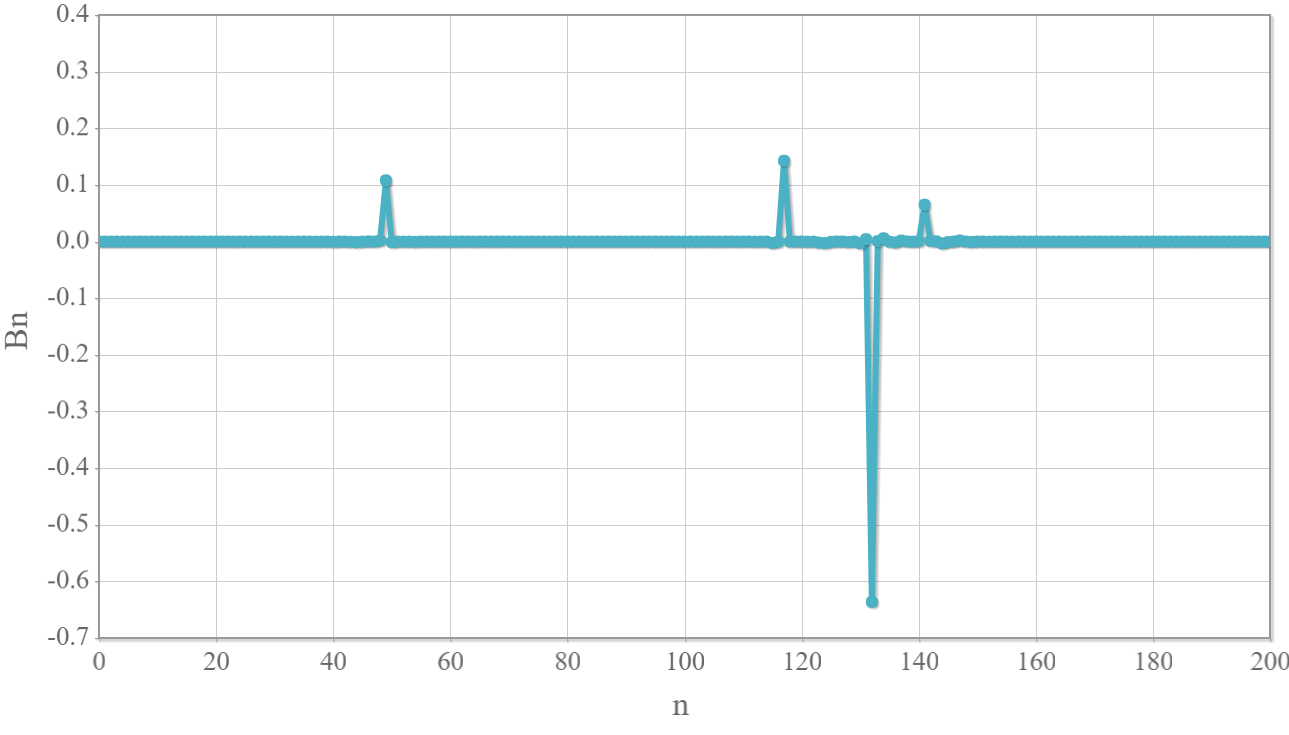
200項まで増やした結果、かなり強い回転運動を実現することができました。 展開係数の値を調べると、$n=117$に大きなピークと$n=47$と$n=138$に小さめのピークがあり、この３つだけで９０％程度を締めていることが確認できました。

強制単振子の力学的エネルギーが最大となった運動

展開係数の値

（追記２）振動の振幅を半分にした場合

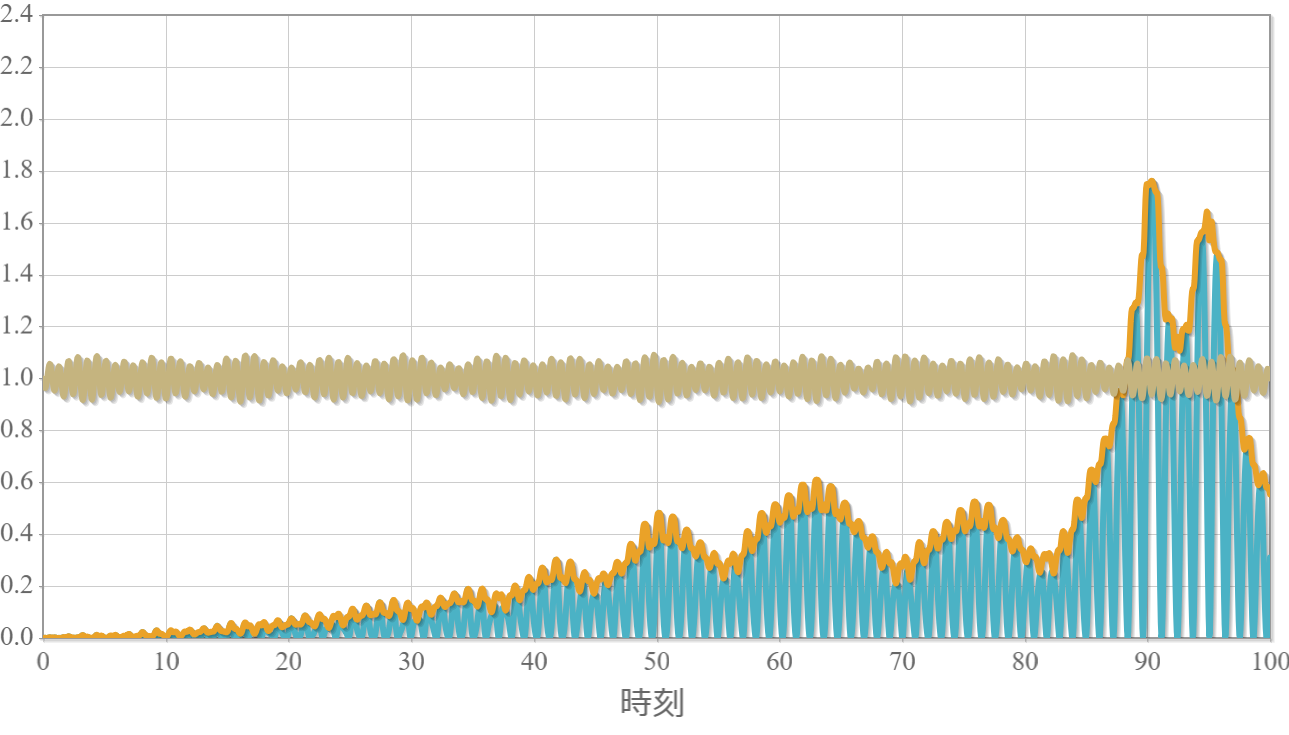
上記のアルゴリズムを用いて、$l=0.1$の場合でも回転する条件があるかを調べました。計算時間を１００秒までとして、一番力学的エネルギーが高くなった運動と展開係数は次のとおりです。$l=0.1$の場合には回転まで至ることはできませんでした。

強制単振子の力学的エネルギーが最大となった運動

展開係数の値

プログラムソース（C++）

・ForcedVibrationSinglePendulumMotion_20060601.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。