【機械学習基礎研究9】
倒立状態維持の強化学習（ランダムな外力を与えた場合）

前回、環境としておもりの位置に加えて速度も定義した結果、行動時間間隔0.05[s]（20Hz）で成功率１００％を達成することができました。 今回は、おもりにランダムな外力（撃力）$\boldsymbol{f}_{\rm ext} $を１秒に１回程度の頻度で与えることで難易度を高めてみます。

Q学習のパラメータ

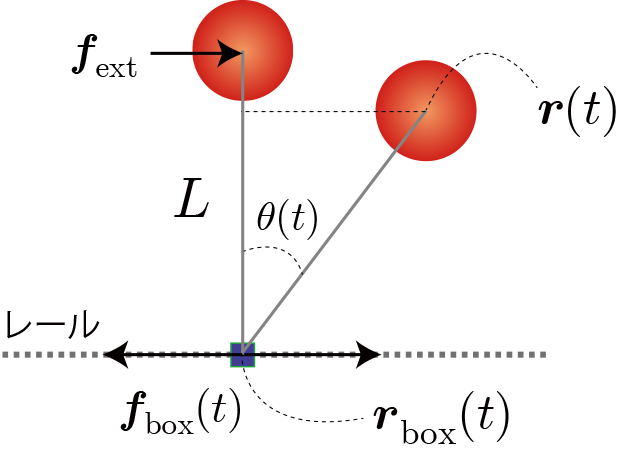
環境と行動と利得の定義（行動価値関数の定義）

・角度の分割数：４
・角速度の分割数：４
→ 環境数４×４
・力の分割数（行動数）：３
→ 最適行動価値関数：４×４×３

利得はおもりの位置エネルギーから運動エネルギーを引いた値（$mgz-1/2 mv^2$）とし、目標達成時（５秒間落下しない）やペナルティー（５秒以内に落下）は与えないことにします。

Q学習の表式とパラメータの値

\begin{align} Q^{(i+1)}(s,a) \leftarrow Q^{(i)}(s,a)+\eta\left[ r+\gamma \max\limits_{a'} Q^{(i)}(s',a') -Q^{(i)}(s,a) \right] \end{align}

$s$ ： 時刻tにおける状態。$s(t)$と同値。
$a$ ： 時刻tにおける行動。$a(t)$と同値。
$r$ ： 時刻tの行動で得られた利得。$r(t+1)$と同値。
$Q(s, a)$ ： 状態$s$における行動aに対する行動価値関数。上付き添字（$i$）は学習回数を表す。
$\gamma$ ： 割引率（$0< \gamma \le 1$）
$\eta$ ： 学習率（$0< \eta \le 1$）
$s'=s(t+1)$

今回の設定

行動時間間隔：0.05（20Hz）（0.05秒ごとに行動を選択・実行する）
学習回数（episode）：1000
割引率（$\gamma$）: 1.0
貪欲性（$\epsilon$）:学習回数0回から500回まで0.5から1.0まで徐々に上げる。それ以降1.0のまま
学習率（$eta$）：学習回数0回から500回まで0.1、それ以降0.01のまま。
外力（ $\boldsymbol{f}_{\rm ext}$ ）

学習結果

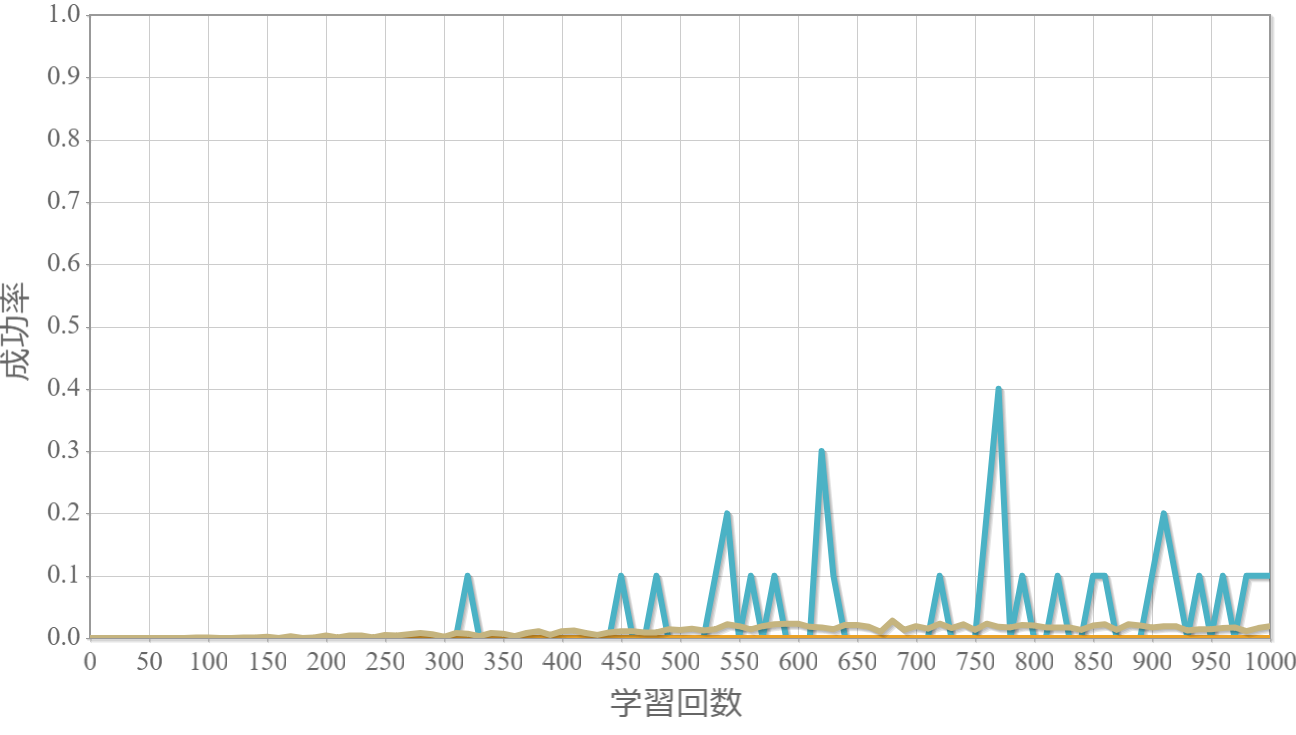
学習回数に対する成功率（100回学習ごとの平均）のグラフを示します。 同じ条件で１０回の学習し、①最も成績が良い結果（青色）、②最も成績が悪い結果（橙色）、③１０回の平均（茶色）の３つを表示します。

外力：0[N]×0.001[s] = 0 [Ns]

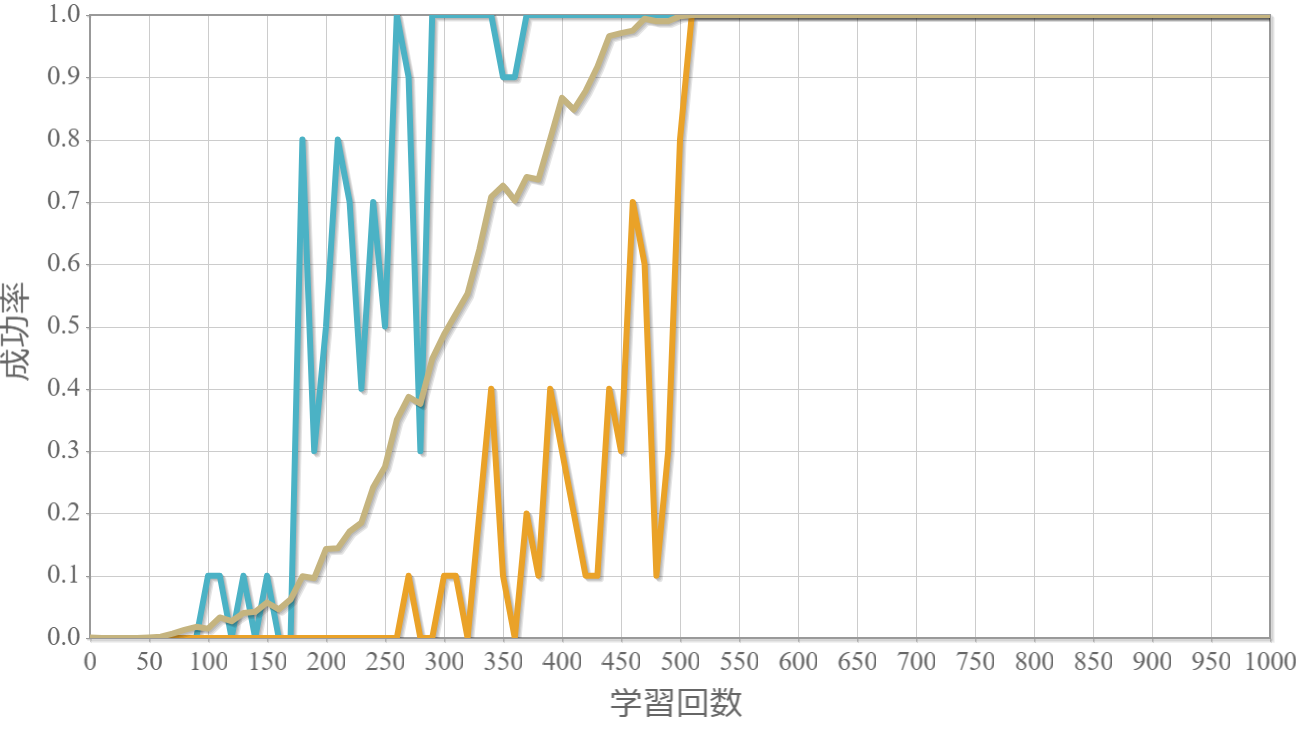
外力：10[N]×0.001[s] = 0.01 [Ns]

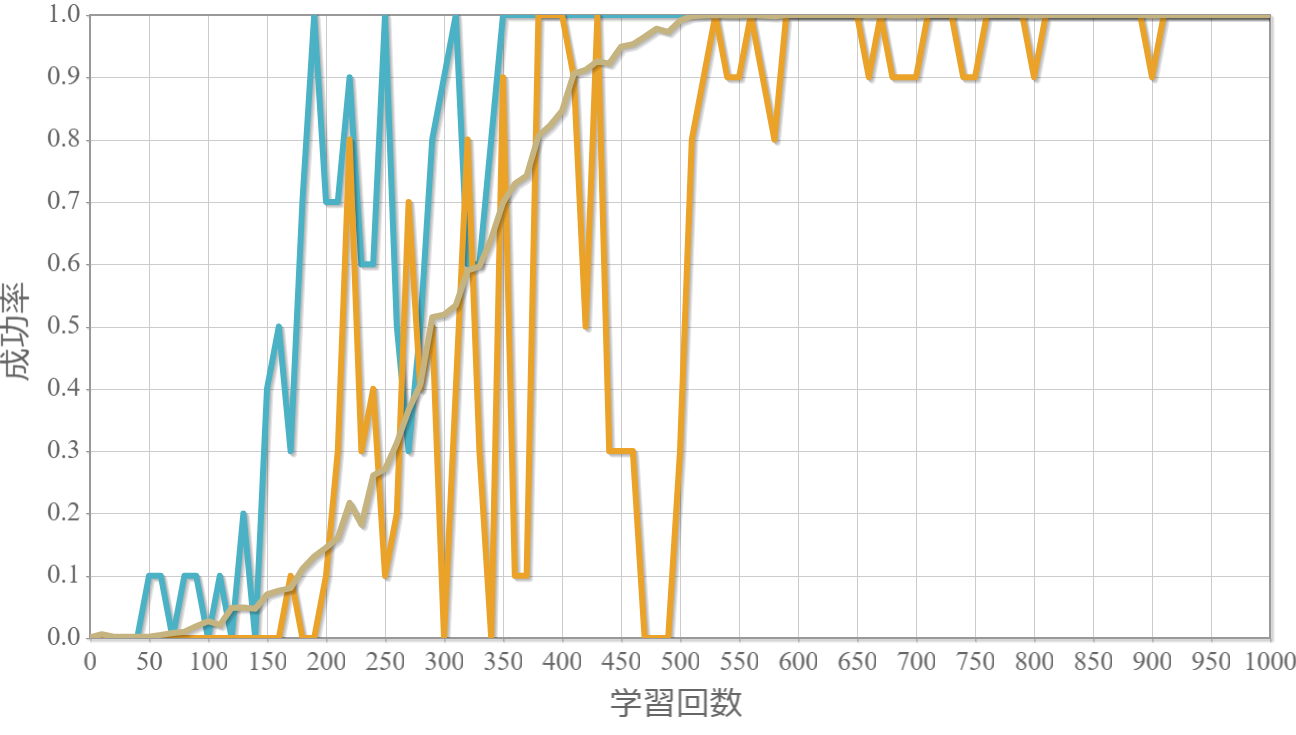
外力：100[N]×0.001[s] = 0.1 [Ns]

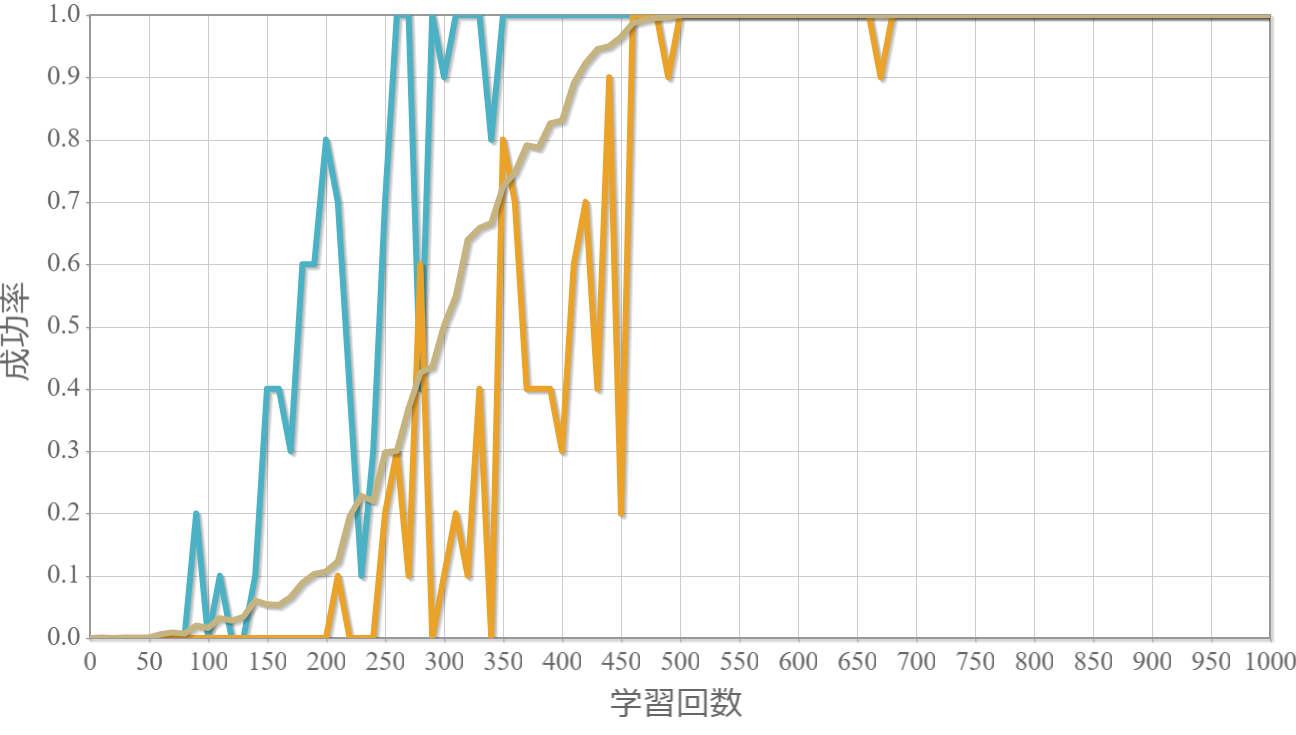
外力：1000[N]×0.001[s] = 1 [Ns]

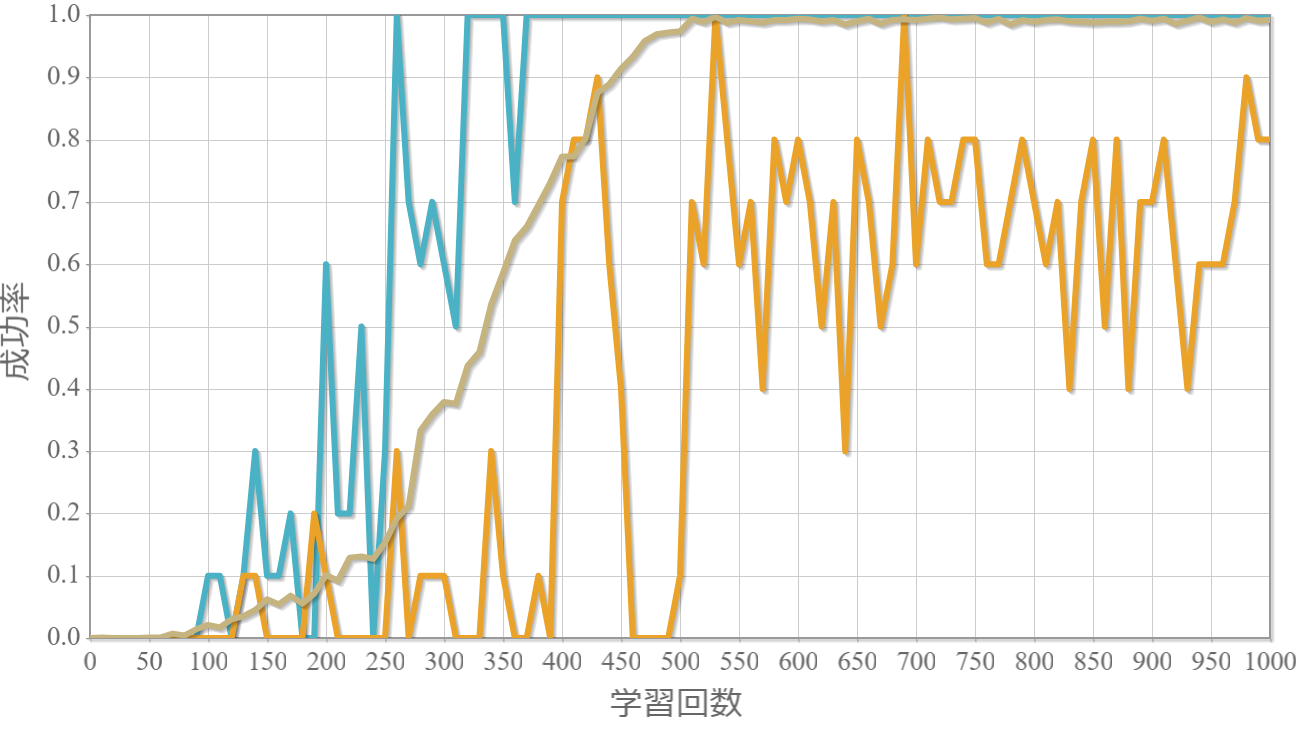
外力：5000[N]×0.001[s] = 5 [Ns]

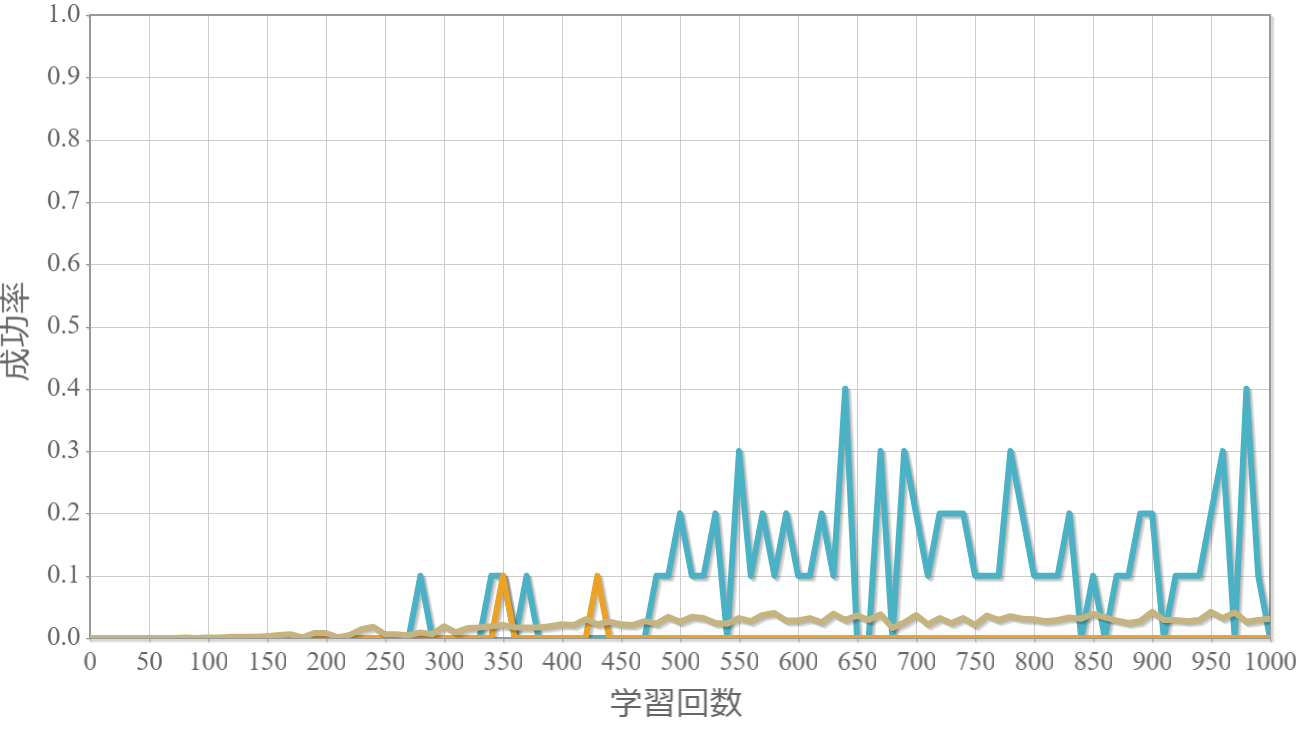
外力：10000[N]×0.001[s] = 10 [Ns]

結果と考察とメモ

外力による力積（力×時間）が5[Ns]を超えると成功率が下がる。
この力積が5[Ns]というのは、おもりの重さが[kg]なのでおもりの速度が瞬間的に5[m/s]変化することを意味します。
【メモ】滑車の位置を原点付近に留まるようにする

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/20180621-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考（物理シミュレーション）

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。