【機械学習基礎研究13】
倒立状態維持の強化学習（原点付近に留まるような環境の与え方）

前々回、振り子を原点近傍に留めるために、原点からの距離の２乗に比例する量（バネ弾性力によるエネルギーに相当）を利得から減点を行いました。が、安定性が悪かったのを改善するため、環境として滑車の速度を加えてみました。 その結果、安定性は圧倒的に改善され、ばね定数$k=1$の場合にはほぼ１００％の成功率を達成することができました。

Q学習のパラメータ

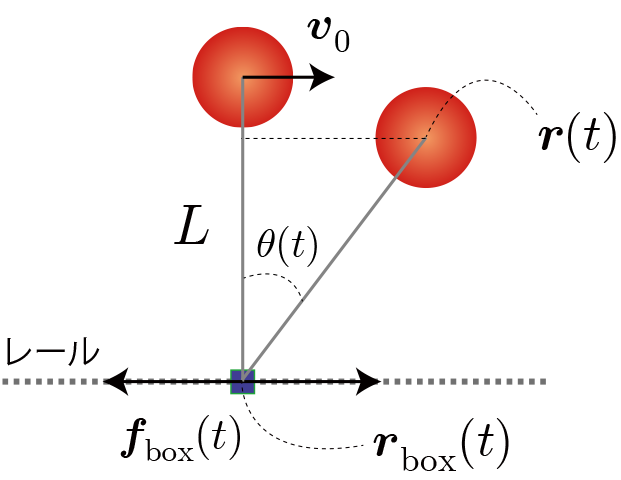
環境と行動と利得の定義（最適行動価値関数の定義）

・おもりの角度の分割数：１１
・おもりの角速度の分割数：７
・滑車の位置の分割数：７
・滑車の速度の分割数：７
→　環境数：１１×７×７×７
・力の分割数（行動数）：５

利得の定義：原点からの距離の２乗に比例する減点項

力学的エネルギー（位置エネルギー＋運動エネルギー）が増大するように、利得として力学的エネルギーをそのまま与えます。 一方、滑車ができるだけ原点近傍に留まってほしいので、原点からの距離の２乗に比例する減点項（バネ弾性力のポテンシャルに相当）を考慮します。

\begin{align} r = mgz + \frac{1}{2} m v^2 - \frac{1}{2} k x^2 \end{align}

第１項目：ポテンシャルエネルギー（加点）、第２項目：運動エネルギー（加点）、第３項目：バネ弾性力ポテンシャル（減点）
成功時や失敗時の加点・減点は行っていません。

Q学習の表式とパラメータの値

\begin{align} Q^{(i+1)}(s,a) \leftarrow Q^{(i)}(s,a)+\eta\left[ r+\gamma \max\limits_{a'} Q^{(i)}(s',a') -Q^{(i)}(s,a) \right] \end{align}

$s$ ： 時刻tにおける状態。$s(t)$と同値。
$a$ ： 時刻tにおける行動。$a(t)$と同値。
$r$ ： 時刻tの行動で得られた利得。$r(t+1)$と同値。
$Q(s, a)$ ： 状態$s$における行動aに対する行動価値関数。上付き添字（$i$）は学習回数を表す。
$\gamma$ ： 割引率（$0< \gamma \le 1$）
$\eta$ ： 学習率（$0< \eta \le 1$）
$s'=s(t+1)$

今回の設定

行動時間間隔：0.05（20Hz）（0.05秒ごとに行動を選択・実行する）
学習回数（episode）：9,000回（残りの1,000回は学習なし）
割引率（$\gamma$）: 1.0
貪欲性（$\epsilon$）:学習回数0回から9,000回まで0.5から1.0まで徐々に上げる。それ以降1.0のまま
学習率（$\eta$）：学習回数0回から9,000回まで0.1、それ以降0。
初速度（ $\boldsymbol{v}_{0}$ ）：-1～1[m/s]でランダムに与える
外力（ $\boldsymbol{f}_{\rm ext}$ ）：なし

学習回数に対する成功確率と軌跡の時系列グラフ

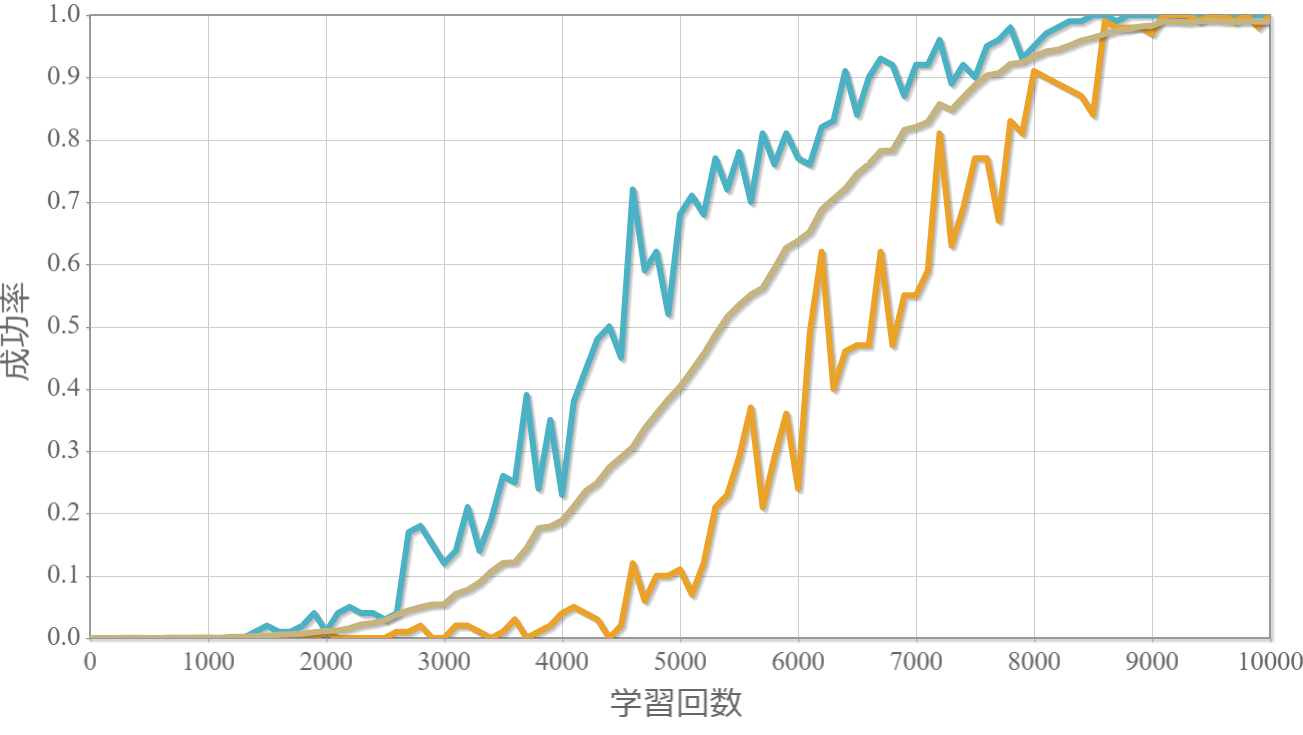
学習回数に対する成功率（100回学習ごとの平均）のグラフを示します。最後の1,000回は貪欲性１として学習結果を評価しています。同じ条件で１００回学習し、①最も成績が良い結果（青色）、②最も成績が悪い結果（橙色）、③１００回の平均（茶色）の３つを表示します。
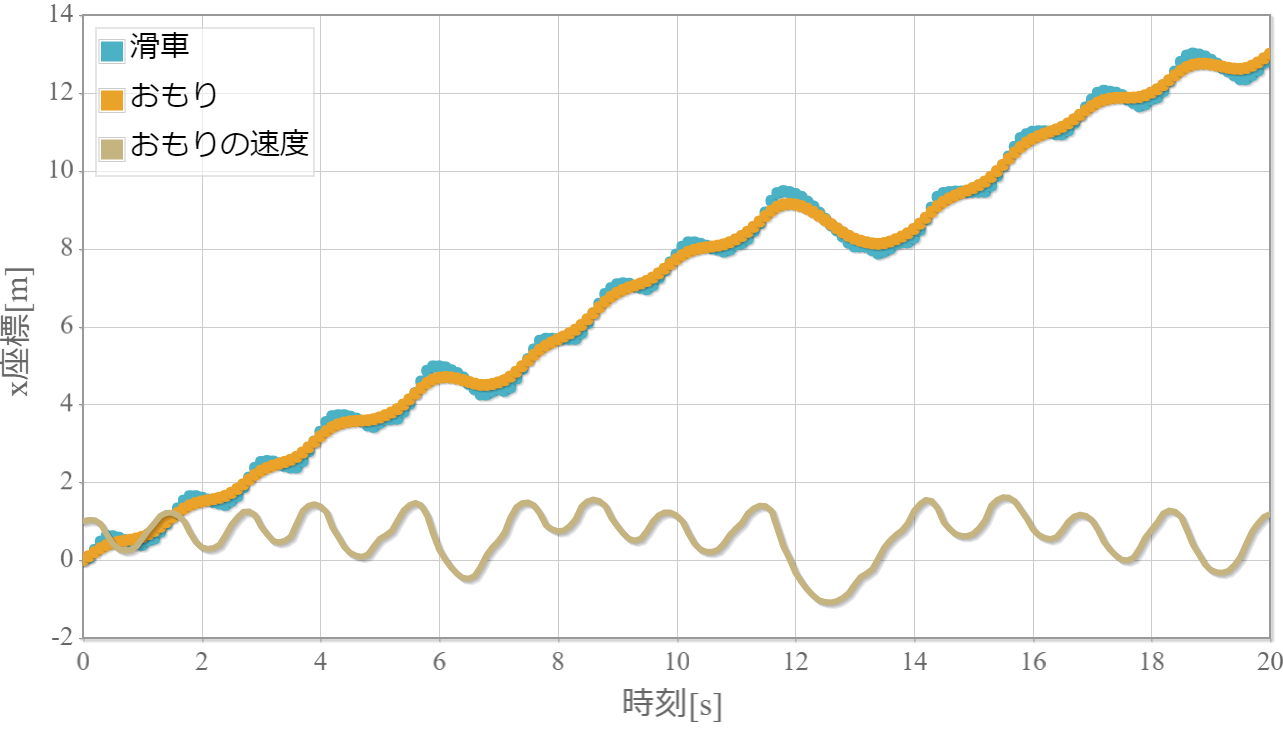
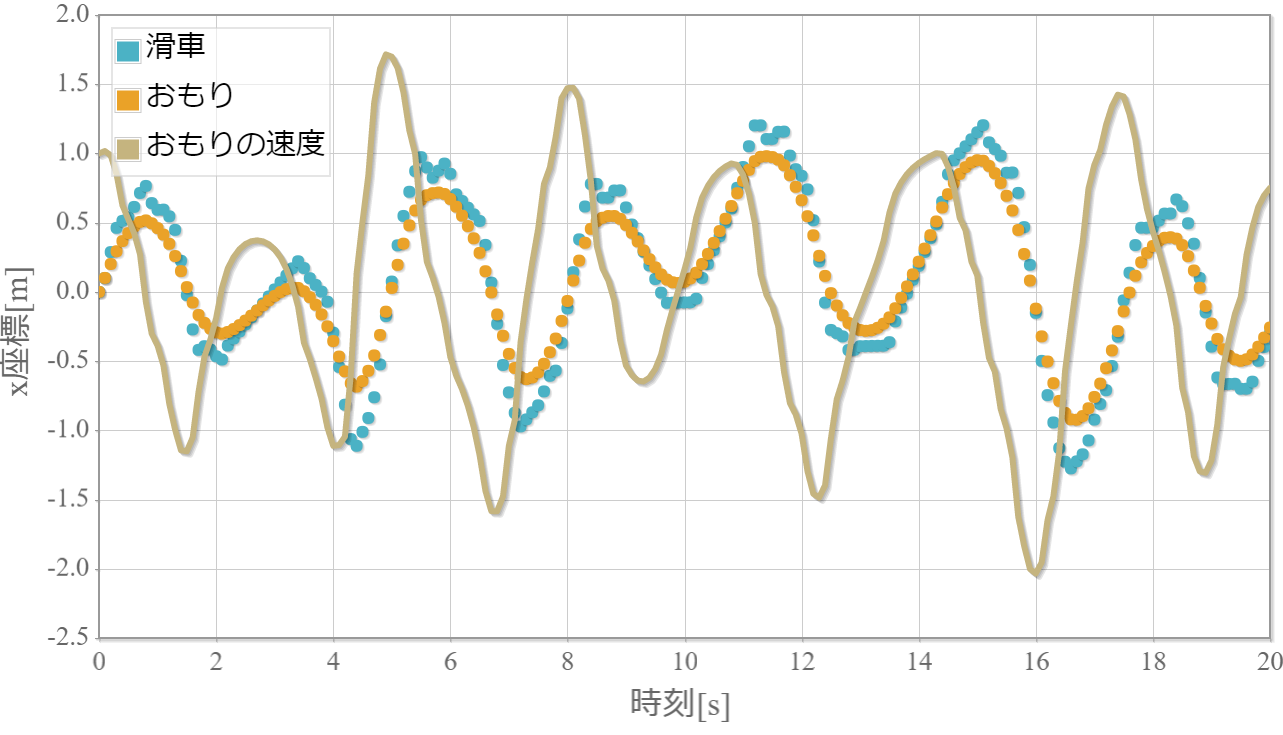
また、軌跡の時系列グラフはおもりの初速度に１を与えた際のその後のおもりと滑車の位置とおもりの速度の時間変化を示しています。

$k=0$（ばね弾性力ポテンシャルなし）の学習回数に対する成功確率

$k=0$（ばね弾性力ポテンシャルなし）のおもりの位置と速度、滑車の位置の時系列データ

$k=1$の学習回数に対する成功確率

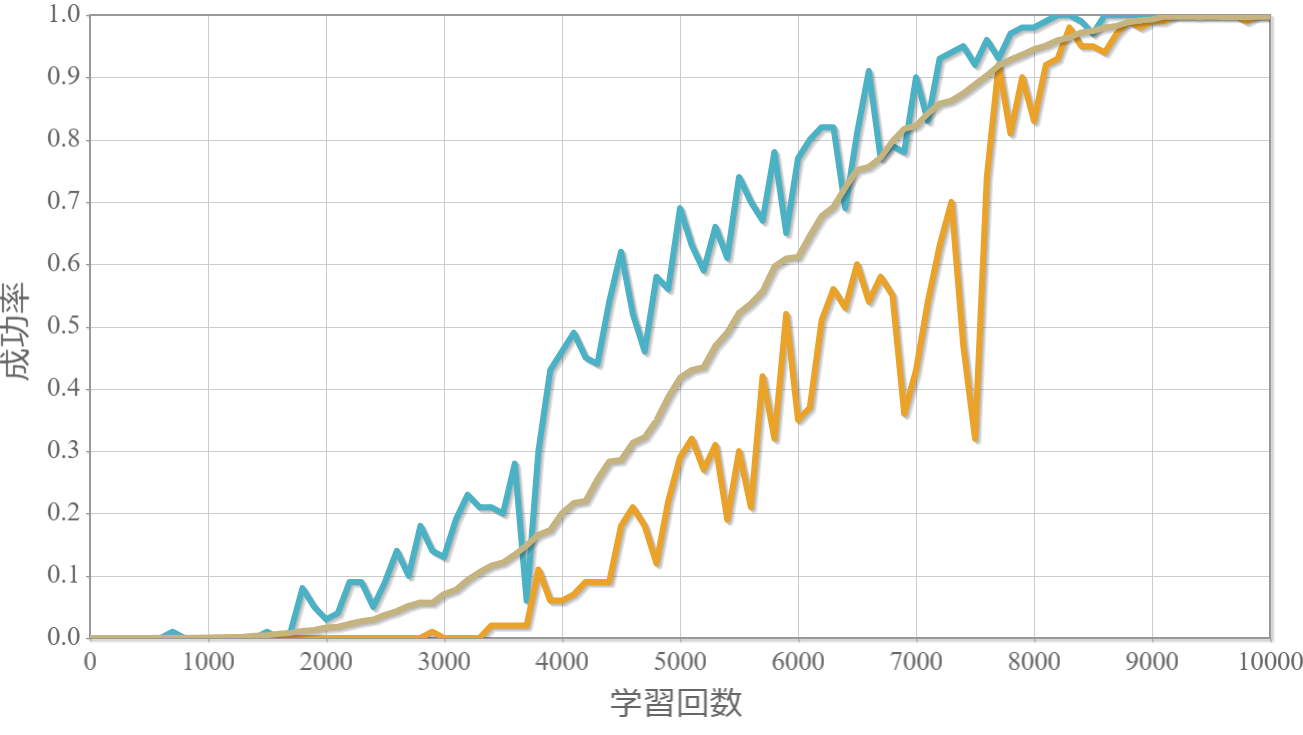
$k=1$のおもりの位置と速度、滑車の位置の時系列データ

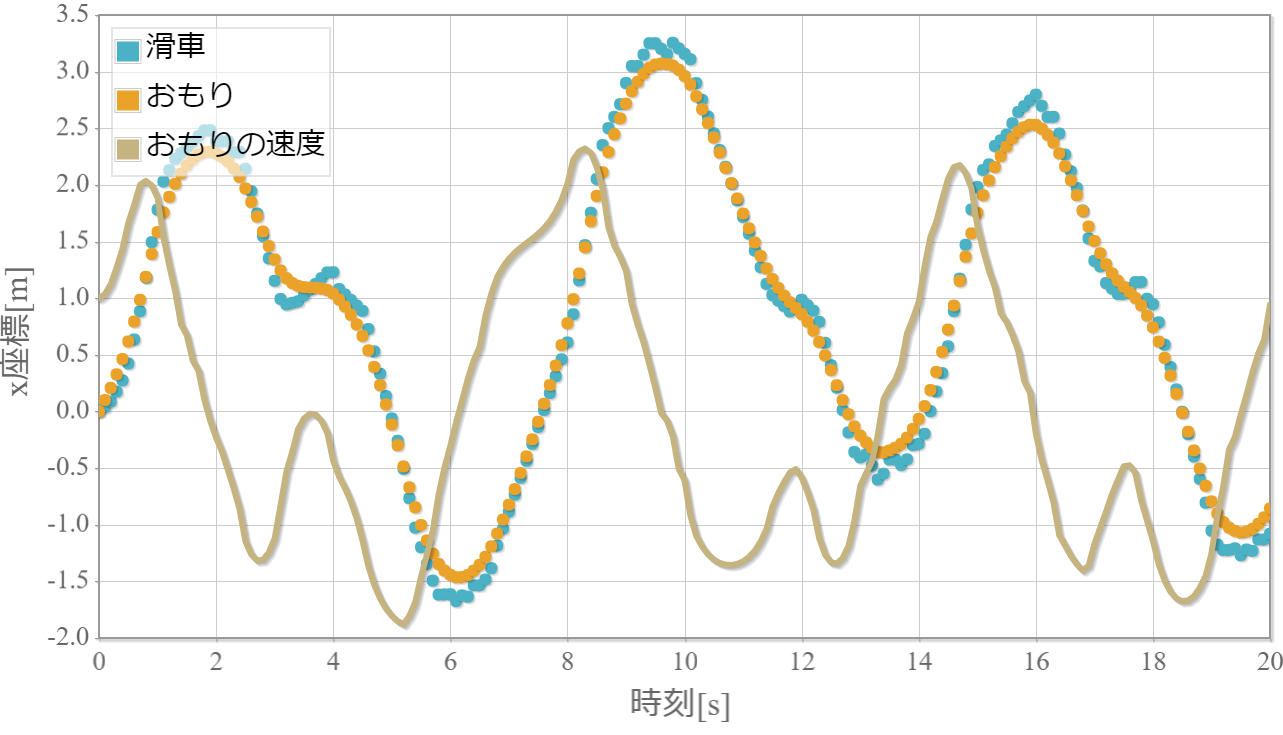
$k=2$の学習回数に対する成功確率

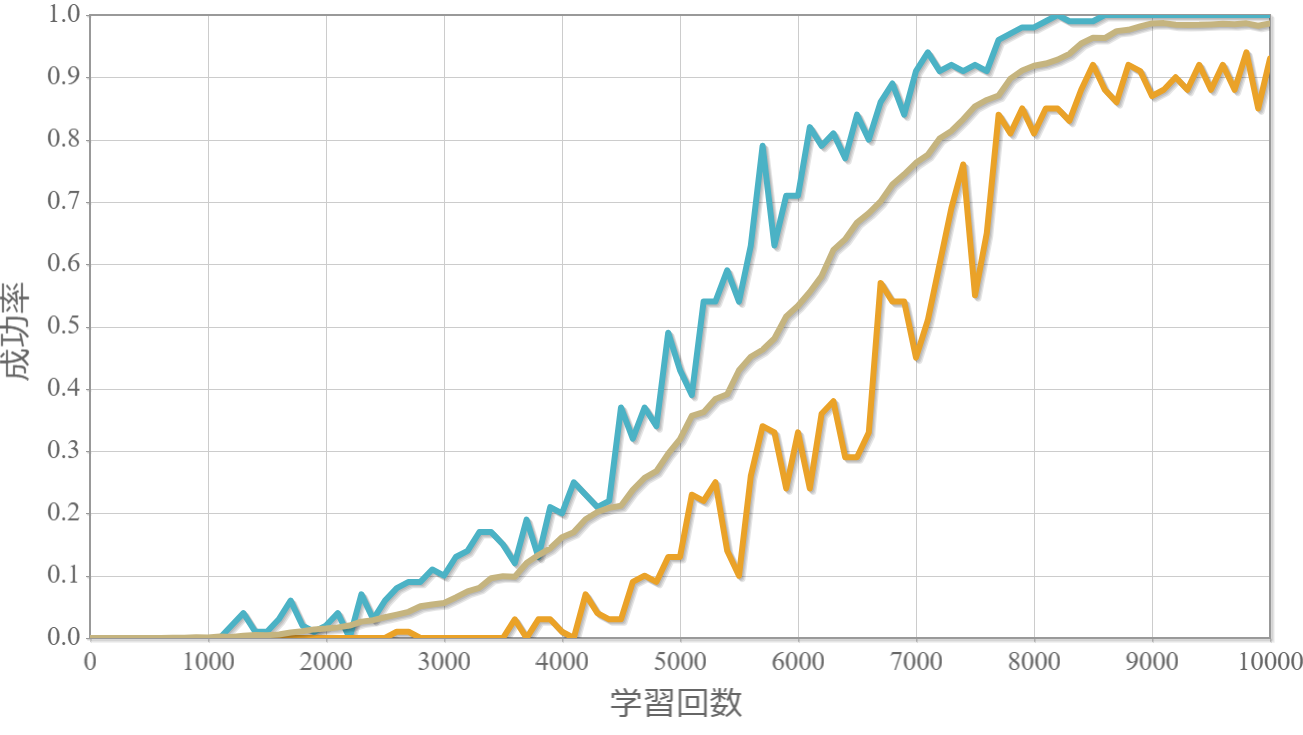
$k=2$のおもりの位置と速度、滑車の位置の時系列データ

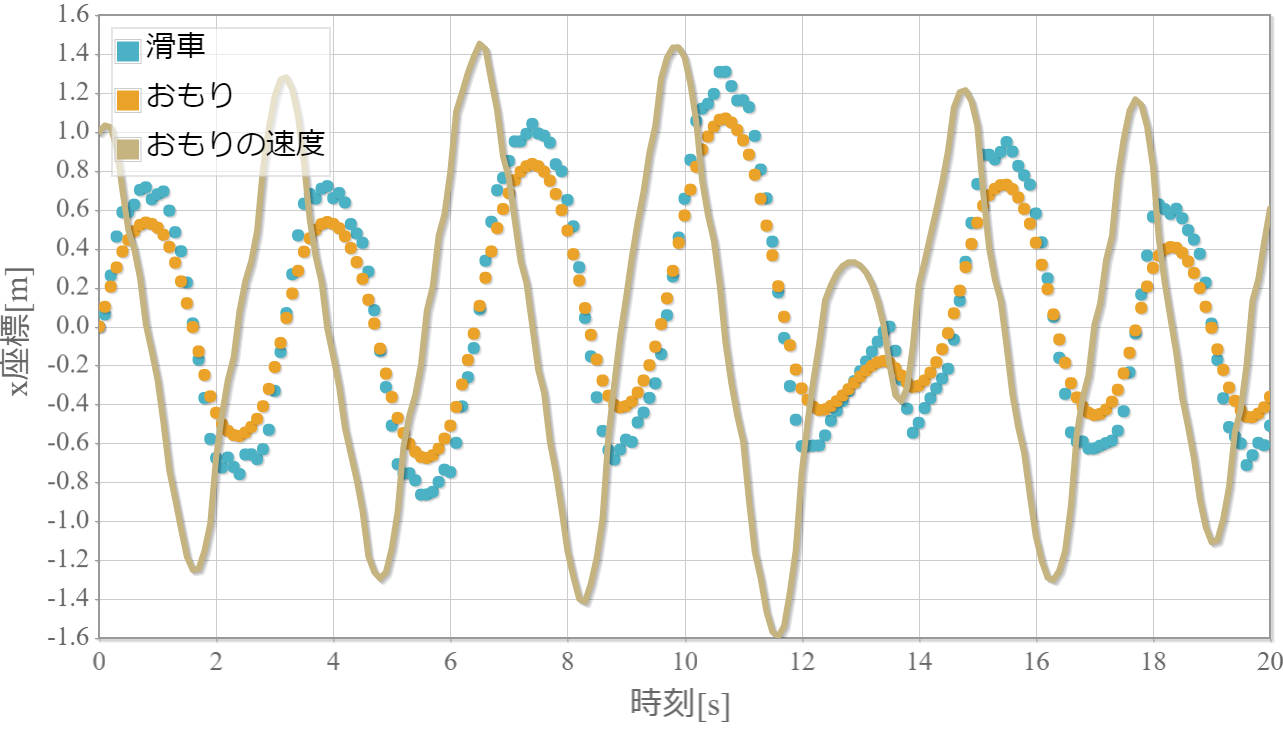
$k=5$の学習回数に対する成功確率

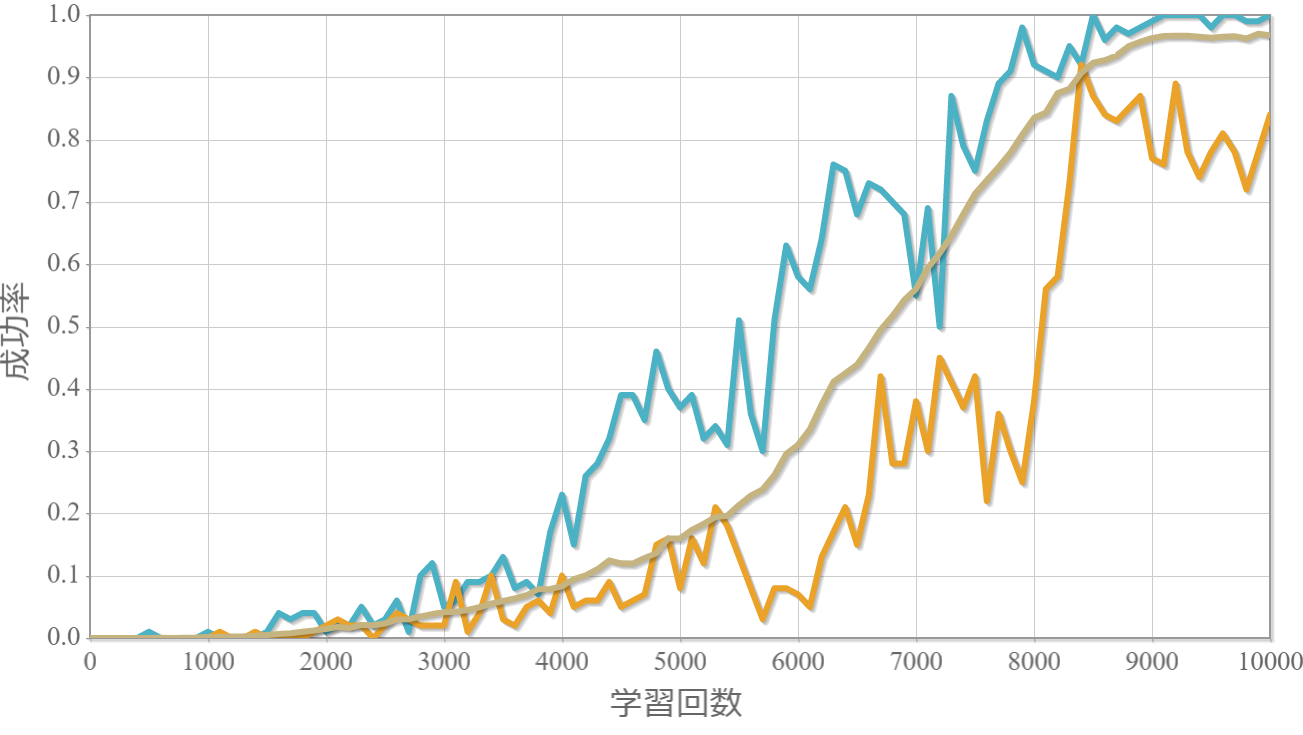
$k=5$のおもりの位置と速度、滑車の位置の時系列データ

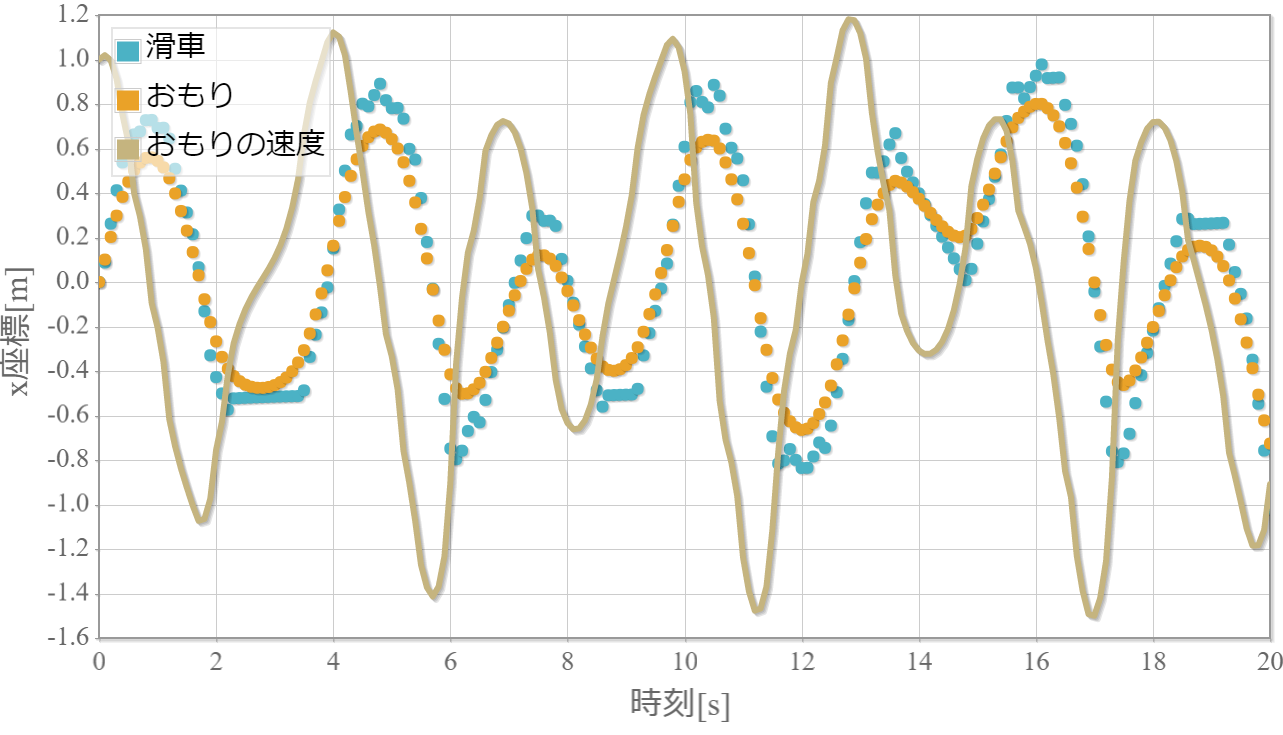
$k=10$の学習回数に対する成功確率

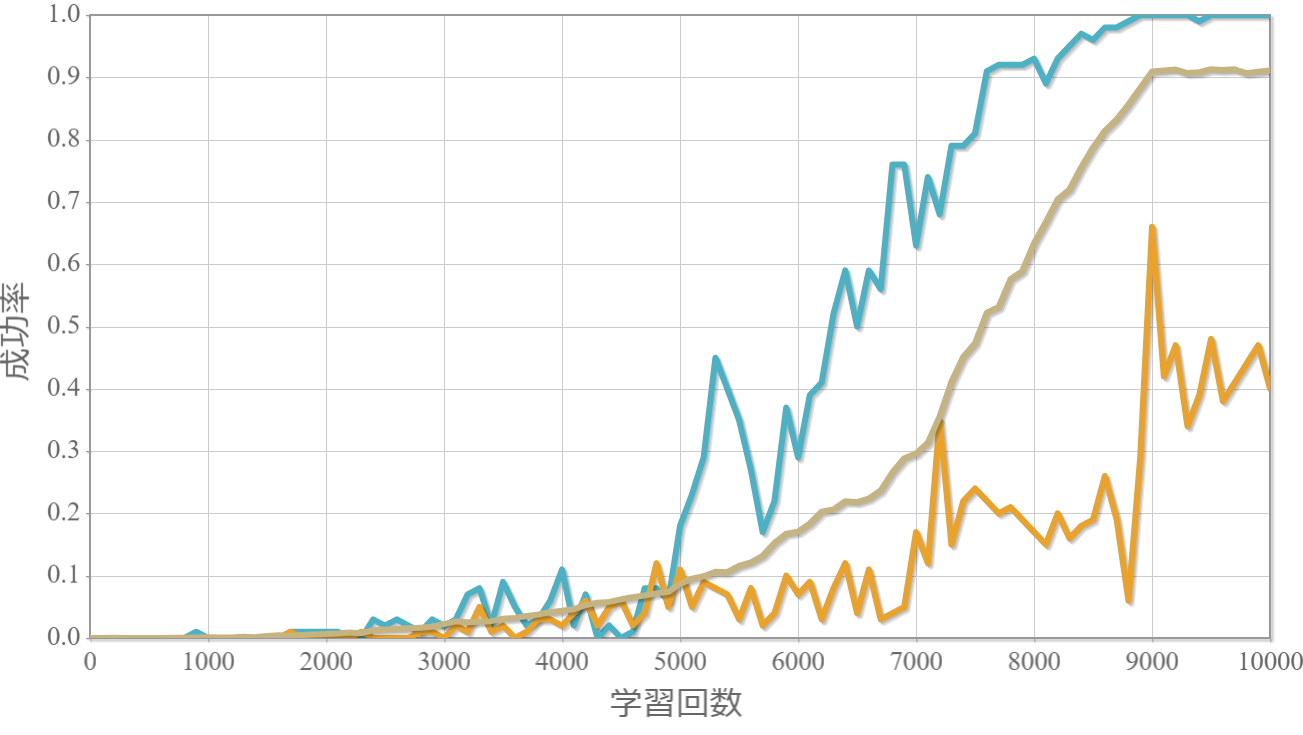
$k=10$のおもりの位置と速度、滑車の位置の時系列データ

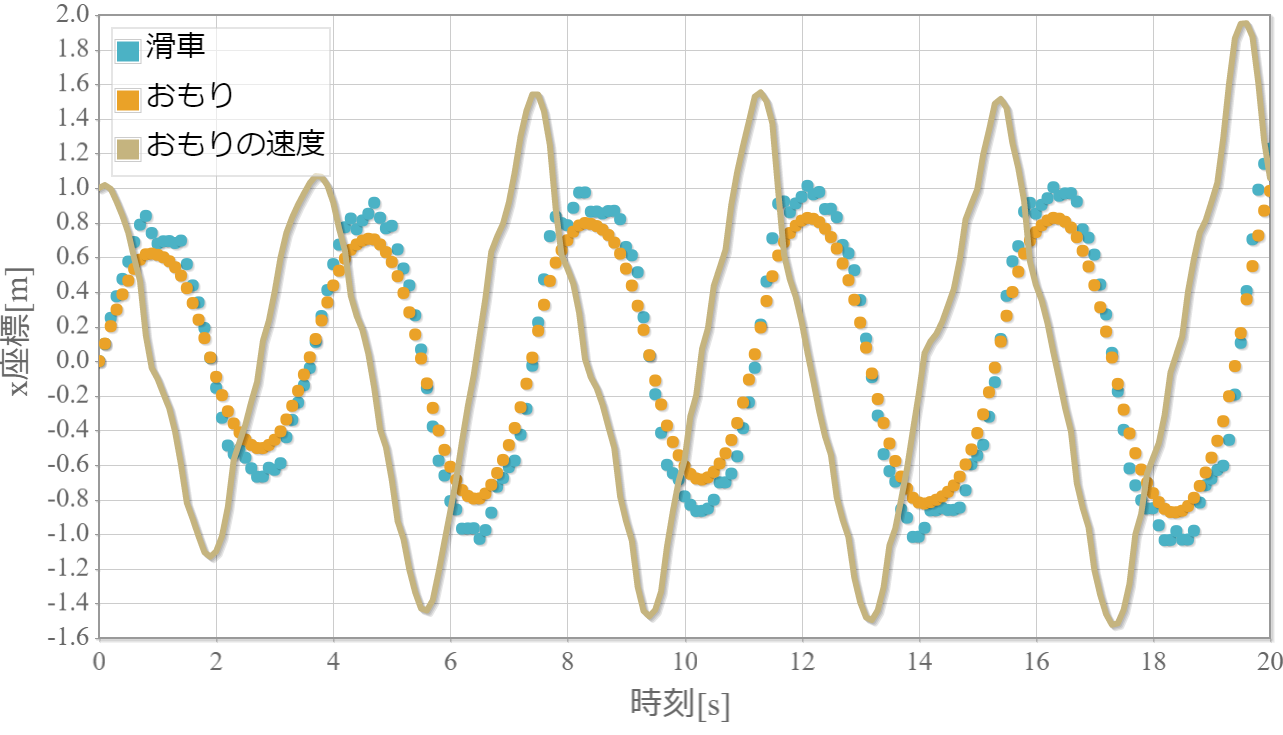
$k=20$の学習回数に対する成功確率

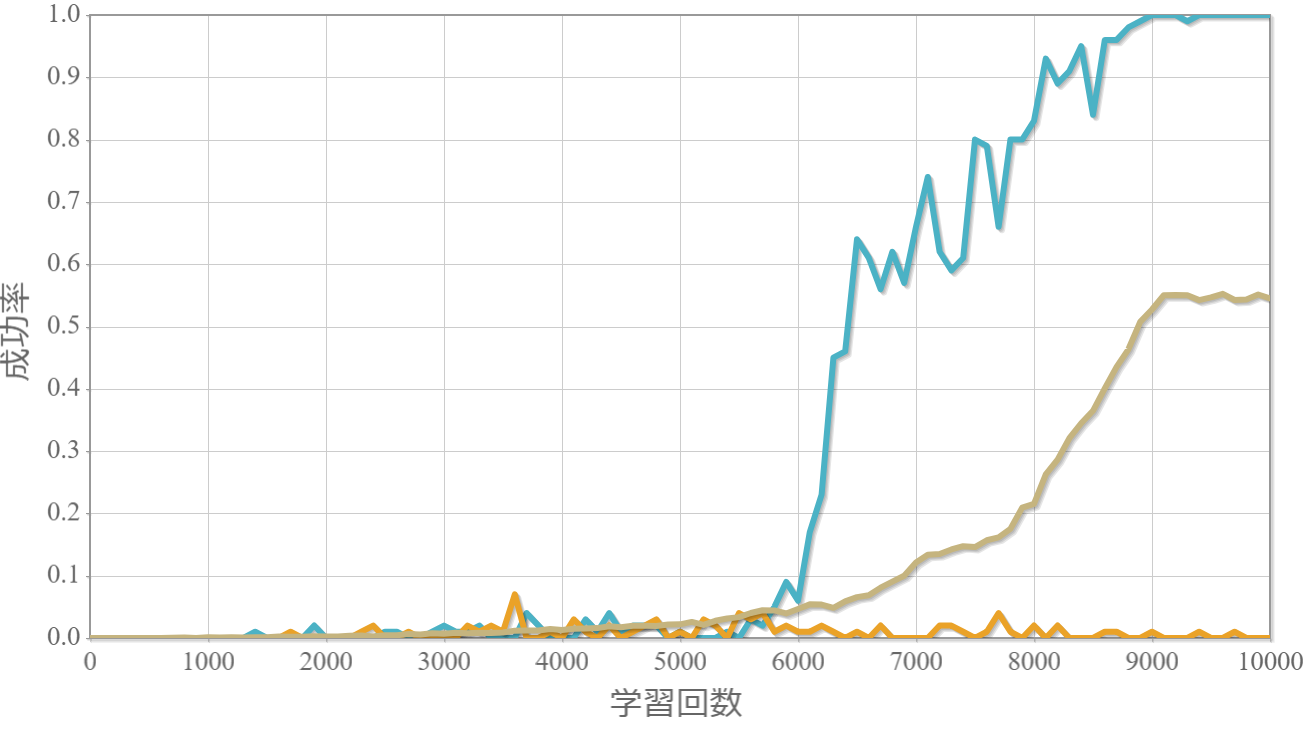
$k=20$のおもりの位置と速度、滑車の位置の時系列データ

結果と考察とメモ

・$k$が大きいほど原点近傍に留めるができる。
・$k$が大きいほど不安定化する。
　→　$k$が大きいほど倒立状態を維持する加点項よりも減点項の寄与が大きくなるため、状況に応じて落下してしまうような誤った学習を行ってしまうと考えられる。
※滑車の速度を環境に加えることでこんなにも成功率が改善されるのは意外でした。
【メモ】減点に向かって収束させるにはどのような学習が必要なのか？

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/20180724-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考（物理シミュレーション）

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。