VisualC++ と OpenGL を利用した仮想物理実験室
シュレディンガー方程式に従う粒子の時間発展：自由粒子

一般的な教科書では、定常状態における議論はなされていますが、時間発展についてはなかなか記述がありません。 シュレディンガー方程式に従う粒子（電子を想定）の時間発展の様子を可視化することを目的に、様々な系におけるシミュレーションを行います。

シュレディンガー方程式

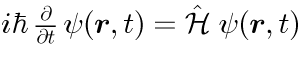
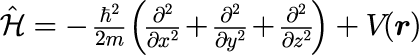
平面波解の重ねあわせ

今回は、もっとも単純な例である「自由粒子」を取り上げます。
波動関数の時間発展を、以下のように平面波の重ね合わせで記述します。

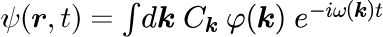
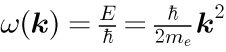
波数空間におけるガウス分布

C_k は一般的には任意ですが、 時間発展を追う上で取扱が容易な「ガウス分布」を取り扱います。 その場合、上式は次のようになります。

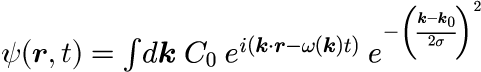
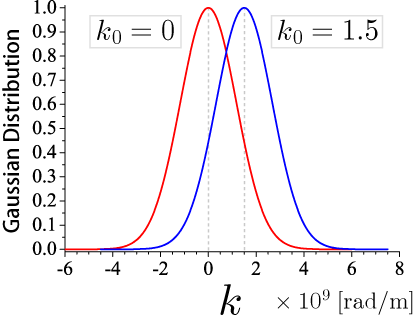
最後の因子が波数空間におけるガウス分布を表します。上式で「k_0」は中心となる波数で、粒子の平均の運動量と関係があります。 本節では、k_0 = 0 の場合と k_0 = 1.5 の場合について考えます（単位は下図を参照）。 下図はガウス分布を表す因子だけをプロットしたものです。

実空間プロット

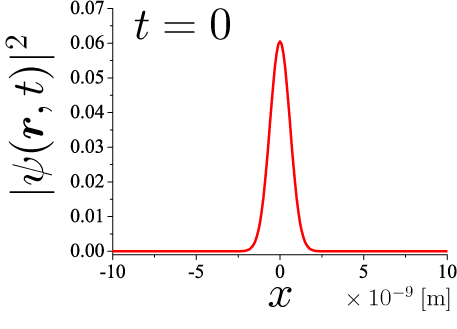
初期状態ととして、1[nm]程度の領域に電子をガウス分布させた状態をとります。
そのためにsigmaの値を調節します。
t=0 の波動関数をプロットしたものが次の図です。

k_0=0 の場合の時間発展

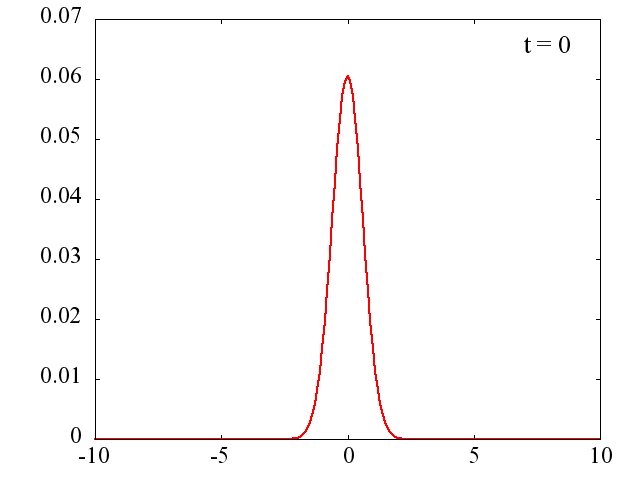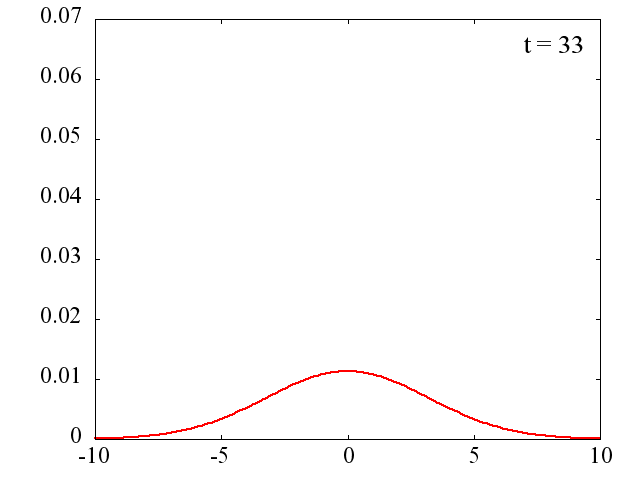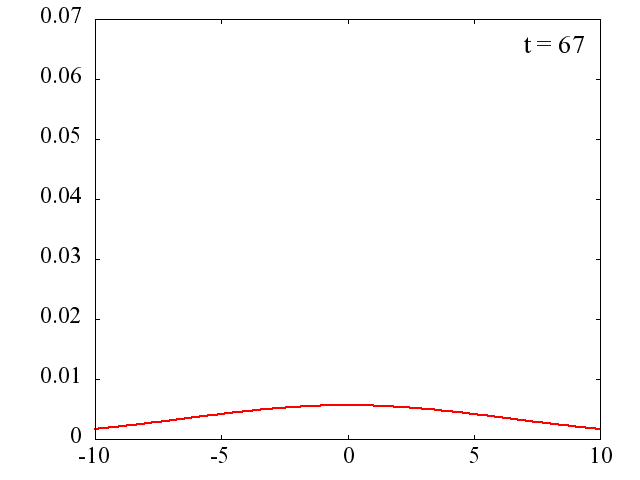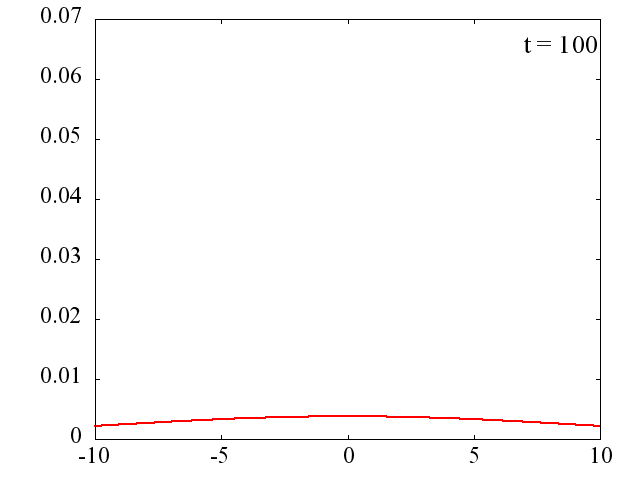
時間間隔は

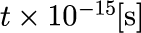
です。 波数 k は様々な値を持つのでパルスは拡散していきます。 k_0=0 、つまり平均の運動量が０の場合には，中心は移動しません。 それにしても、電子はたった 10^{-13}[s]後には拡散してしまいます。

k_0=1.5 の場合の時間発展

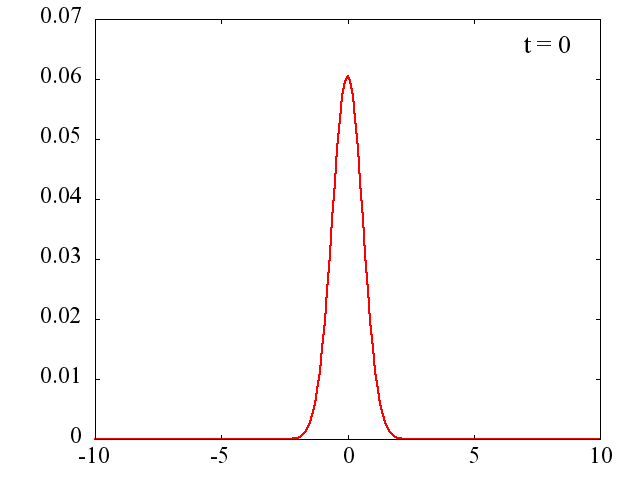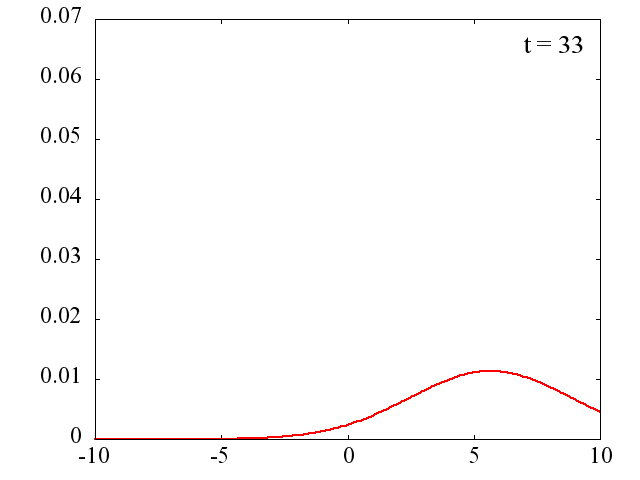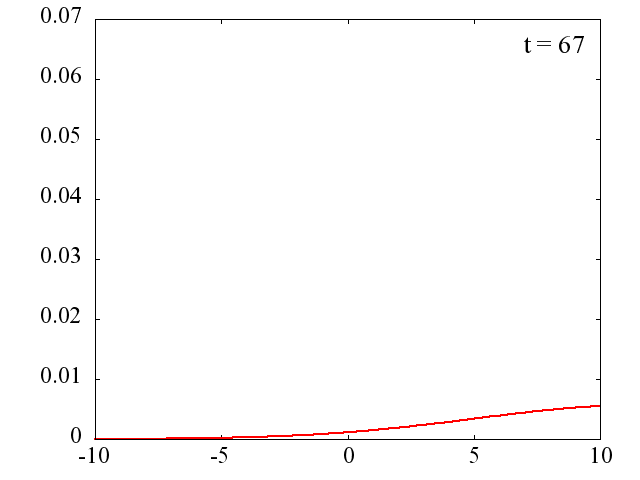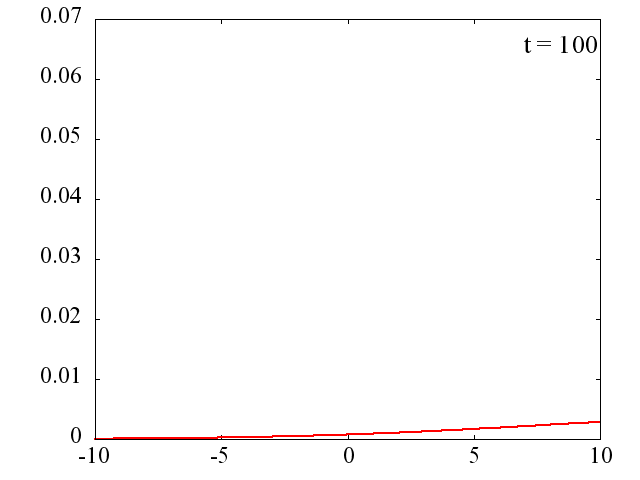
電子は k_0 に対応する平均の運動量を持ちます。 移動時ながら拡散していく様子が分かります。

VisualC++ ＋ gnuplotによるアニメーション

※不必要な変数、インクルードなどが多数ありますので、利用の際はご注意ください。
※VisualC++ から gnuplot を操作する方法をご参照ください。

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <direct.h>
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);

const int N = 1000 , Lx = 200, Ly = 200, Lz = 200;
complex<double> Psi = complex<double>(0.0,0.0) ;

double z = 0.0, x= 0.0, k = 0.0;
const double c = 2.99792458E+8;
const double mu0 = 4.0*PI*1.0E-7;
const double epsilon0 = 1.0/(4.0*PI*c*c)*1.0E+7;
const double h  = 6.6260896 * 1.0E-34;
double hbar = h/(2.0*PI);
const double me = 9.10938215 * 1.0E-31;

int tn = 0 , t0 =0, te = 10;

double dz = 1.0E-10;
double dz_ = 1.0E-9;
double dk_ = 1.0/(dz_);
double dt = 1.0E-13/(double(te+1))  ,ts;
double dk = 1.2/(dz*double(N));
complex<double> k0 = 0.15/dz;
double sigma = sqrt(log(2.0))/(dz_);


string folder = "1", ff="", fg="";  //保存フォルダ名
ostringstream fname;

int main(){
  _mkdir(folder.c_str());
	ff = folder + "/K.data";    ofstream fout_K( ff.c_str()); 

  complex<double> KK = complex<double>(0.0,0.0) ;

  for(tn=t0; tn<=te; tn++){
    double t = dt * double(tn) ;
    cout << tn << endl;

    ostringstream fname_Psi;
    fname_Psi <<  folder   + "/" << tn << ".data";//出力ファイル名
    string f_Psi = fname_Psi.str();
    ofstream fout_Psi;
    fout_Psi.open(f_Psi.c_str());

    for(int ix= -Lx/2; ix<= Lx/2; ix++){
      Psi = complex<double>(0.0,0.0);
      x = dz * ix;

      for(int jz= -N/2; jz<= N/2 ; jz++){
        complex<double> k = k0 + dk*double(jz);
        double omega = hbar/(2.0*me) * pow(abs(k),2);
        if(ix==0){
          KK = exp( -pow((k-k0)/(2.0*sigma),2) );
          fout_K << k.real()/dk_  << " "<< KK.real() << endl;
        }
        Psi += exp( I* (k*x - omega * t) -pow((k-k0)/(2.0*sigma),2) );
      }
      Psi = Psi/ double(N);
      fout_Psi<< x/dz_  << " "<<  pow(abs(Psi),2) << endl;
    }

    FILE *fp = _popen( "C:/gnuplot/bin/pgnuplot.exe" , "w");

	  if (fp == NULL) return -1; 
	  fputs("set terminal gif\n", fp);
	  fputs("set tics font \'Times,18\'\n", fp);
	  fputs("set rmargin 4\n", fp);
  	fputs("set nokey\n", fp); 
	  fputs("set yr[0:0.07]\n", fp);
	  fname  << "set label \'t = " << tn << "\'  font \'Times,20\'  at 7 , 0.065 \n"  ;
	  fg = fname.str();
	  fputs(fg.c_str(), fp);
	  fname.str("");
		fname  << folder + "/" <<  tn+1000 << ".gif"  ;
	  fg = fname.str();
	  fg = "set output '" + fg + "'\n";
	  fputs(fg.c_str(), fp);
	  fname.str("");
	  fname <<  folder + "/" << tn << ".data" ;//<------------------------------入力ファイル名
	  fg = fname.str();
	  fname.str("");
    fg = "plot \"" + fg + "\" u 1:2 w l lw 2\n";
	  fputs(fg.c_str(), fp);
	  fflush(fp);

		_pclose(fp);
  }
	return 0;
}