シュレディンガー方程式に従う粒子の時間発展
無限に深い井戸型ポテンシャルの時間発展２
文責：遠藤 理平 （2010年9月25日）
カテゴリ：仮想物理実験室(325)
シュレディンガー方程式に従う粒子の時間発展２：無限に深い井戸型ポテンシャルでは、中心波数を変えた時の運動の違いを見てみた。今回は、電子のパルス幅を変化させた時の運動の違いを見てみます。
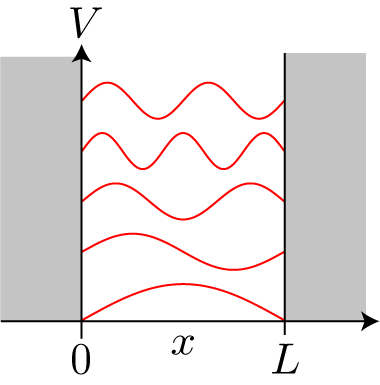
無限に深い井戸型ポテンシャル
無限に深い井戸型ポテンシャルによる固有波動関数の重ねあわせ
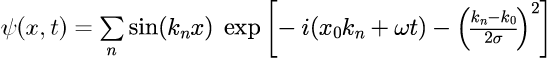
x_0 : パルスの初期中心座標
パルス幅はガウシアンの肩にある sigma の値で決まります（σ→大 ⇔パルス幅→小）。
k_n は境界条件から次のようになります。
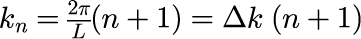
ガウス分布（波数空間）の幅と波動関数（実空間）の幅の関係
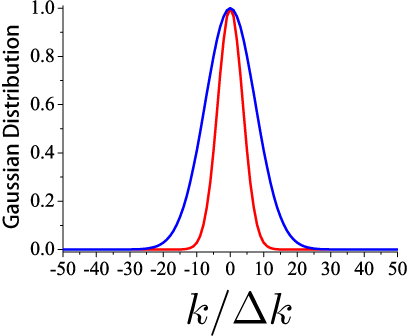
σの値が次の２つの場合の、ガウス分布（波数空間）と実空間の波動関数の幅を見てみる。
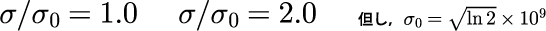
ガウス分布（波数空間）
σ=2 (青)
σ=1 (赤)
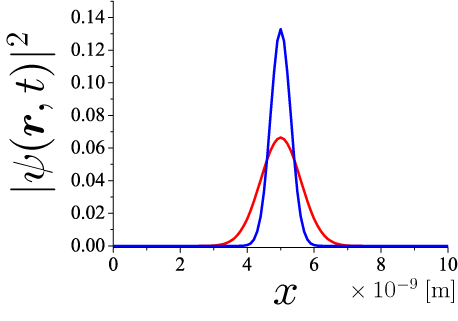
波動関数（実空間）
t=0 における波動関数の分布
無限に深い井戸型ポテンシャルの波動関数の時間発展
初期パルス幅の違いにより、時間発展の様子が異なります。
しかしながら、周期は同じであることがわかった（周期:約130[fs]）。
