【機械学習基礎研究15】
最下点からの強制振動で倒立状態への強化学習（利得の与え方と学習手順）

「倒立状態維持の強化学習」、「最下点からの強制振動の強化学習」を経て、今回ようやく、中間目的としていました「最下点に静止した振り子を強制振動させて倒立状態を維持する強化学習」に到達しました。本稿ではその強化学習の利得の与え方と学習手順について報告します。

Q学習のパラメータ

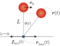
環境と行動と利得の定義（最適行動価値関数の定義）

・おもりの角度の分割数：２１
・おもりの角速度の分割数：７
・滑車の位置の分割数：７
・滑車の速度の分割数：７
→　環境数：２１×７×７×７
・力の分割数（行動数）：５

利得の定義

今回の強化学習を成功させるには目的の異なる２つの利得の定義が必要となります。１つ目は最下点から振り子を強制振動させるモード（強制振動モード）、２つ目は倒立状態を維持するモード（倒立維持モード）です。 そのため、利得の定義は場合分けが必要になると考えられます。

共通利得項

・倒立状態を維持　→　おもりの位置エネルギーを加点項
・振り子を原点付近に留める　→　原点からの距離の２乗に比例する減点項（バネ弾性力のポテンシャルに相当）

強制振動モードの利得項

・おもりの運動を大きくする（速度を早くする）　→　おもりの運動エネルギーを加点項

倒立維持モードの利得項

・おもりの運動を大きくする（速度を早くする）　→　おもりの運動エネルギーを減点項

２つのモードの切替の判定基準

今回、おもりの位置が水平以下の場合に強制振動モード、水平より上の場合に倒立維持モードとします。

■強制振動モードの利得（$ z<= L $）

\begin{align} r = mgz - \frac{1}{2} k x^2 + \frac{1}{2} m v^2 \end{align}

■倒立維持モードの利得（$ z > L $）

\begin{align} r = mgz - \frac{1}{2} k x^2 - \frac{1}{2} m v^2 \end{align}

学習方法

今回２つのモードを効率よく学習するために、おもりの初期状態を倒立状態（初速度ランダム）と最下点（初速度０）の２つを交互に与えます。 成功判定はどちらの初期状態の場合も、開始から５秒後に倒立状態であるか（おもりの位置の高さが $z > L \times 1.95$ ）とします。

Q学習の表式とパラメータの値

\begin{align} Q^{(i+1)}(s,a) \leftarrow Q^{(i)}(s,a)+\eta\left[ r+\gamma \max\limits_{a'} Q^{(i)}(s',a') -Q^{(i)}(s,a) \right] \end{align}

$s$ ： 時刻tにおける状態。$s(t)$と同値。
$a$ ： 時刻tにおける行動。$a(t)$と同値。
$r$ ： 時刻tの行動で得られた利得。$r(t+1)$と同値。
$Q(s, a)$ ： 状態$s$における行動aに対する行動価値関数。上付き添字（$i$）は学習回数を表す。
$\gamma$ ： 割引率（$0< \gamma \le 1$）
$\eta$ ： 学習率（$0< \eta \le 1$）
$s'=s(t+1)$

今回の設定

行動時間間隔：0.05（20Hz）（0.05秒ごとに行動を選択・実行する）
学習回数（episode）：18,000回（残りの2,000回は学習なし）
割引率（$\gamma$）: 1.0
貪欲性（$\epsilon$）:学習回数0回から18,000回まで0.5から1.0まで徐々に上げる。それ以降1.0のまま
学習率（$\eta$）：学習回数0回から18,000回まで0.1、それ以降0。
初速度（ $\boldsymbol{v}_{0}$ ）：初期状態が倒立状態の場合のみ-1～1[m/s]でランダムに与える
外力（ $\boldsymbol{f}_{\rm ext}$ ）：なし

学習回数に対する成功確率と力学的エネルギー（運動エネルギーと位置エネルギーの和）の時系列グラフ

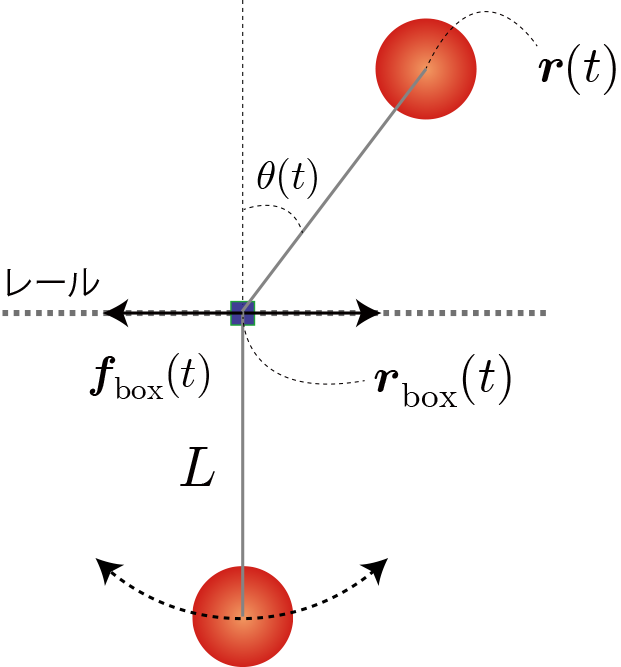
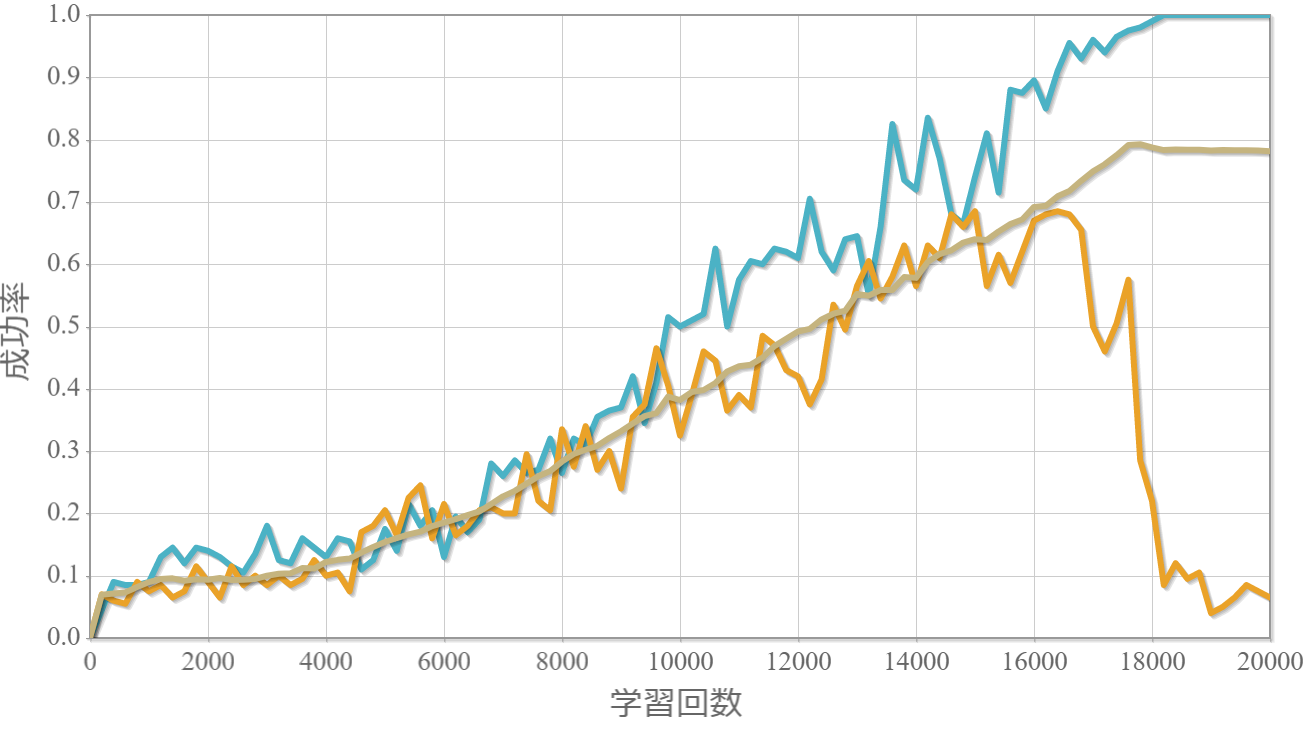
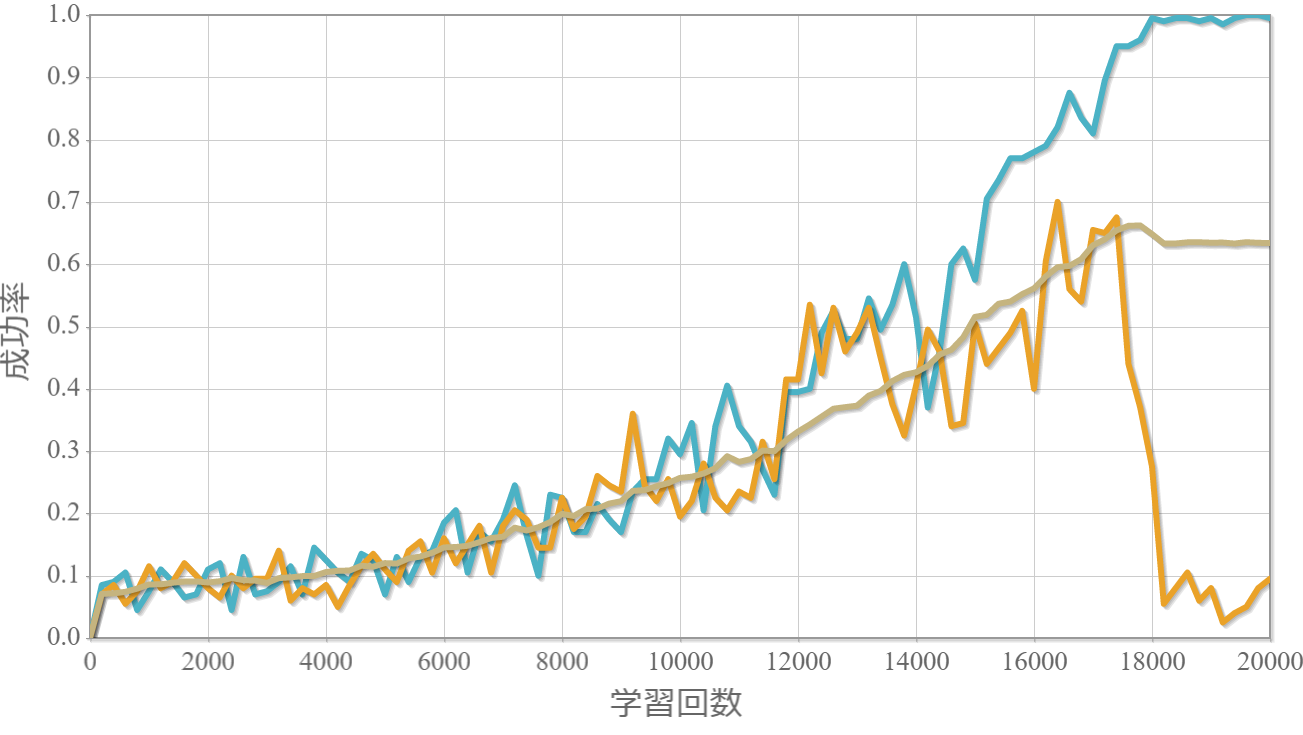
学習回数に対する成功率（100回学習ごとの平均）のグラフを示します。最後の2,000回は貪欲性１として学習結果を評価しています。同じ条件で１００回学習し、①最も成績が良い結果（青色）、②最も成績が悪い結果（橙色）、③１００回の平均（茶色）の３つを表示します。
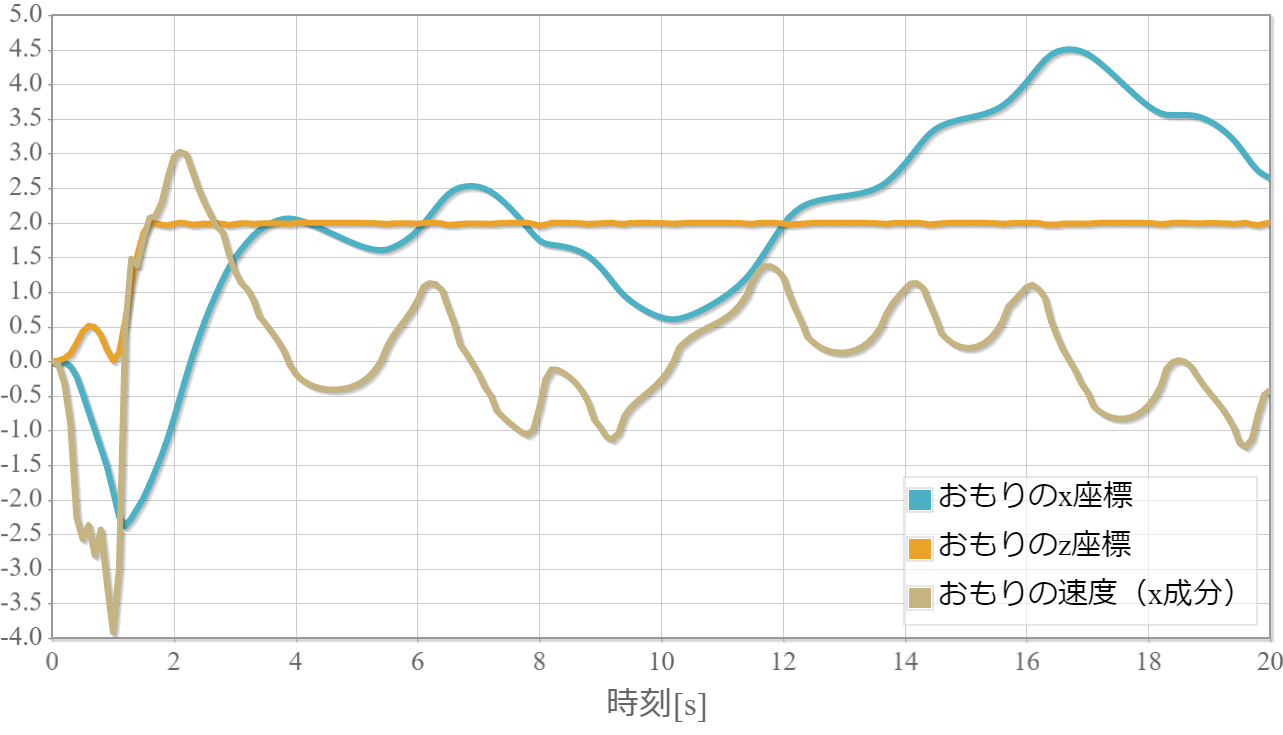
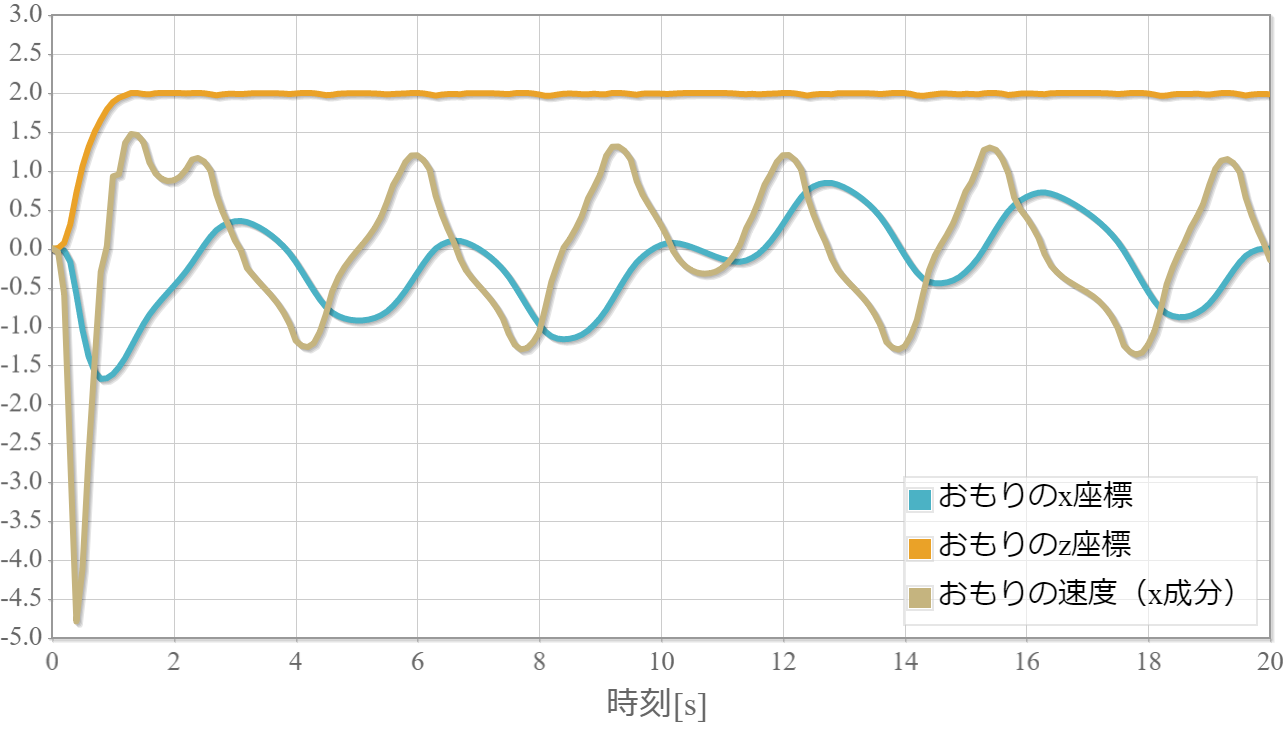
また、力学的エネルギーの時系列グラフは振り子の運動エネルギーと位置エネルギーと力学的エネルギーの時間変化、また参考までに振り子の位置（x座標）の時間変化を示しています。

$k=1$の学習回数に対する成功確率

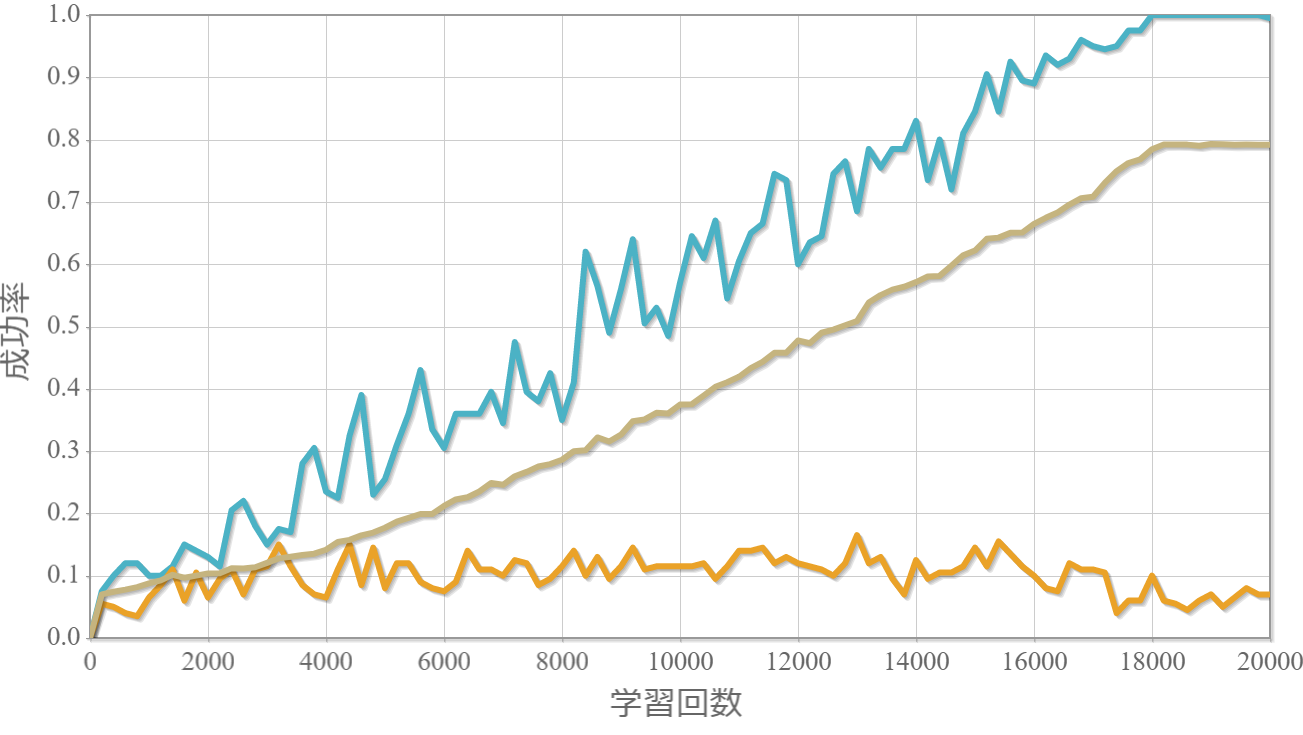
$k=1$の力学的エネルギーと振り子の位置の時系列データ

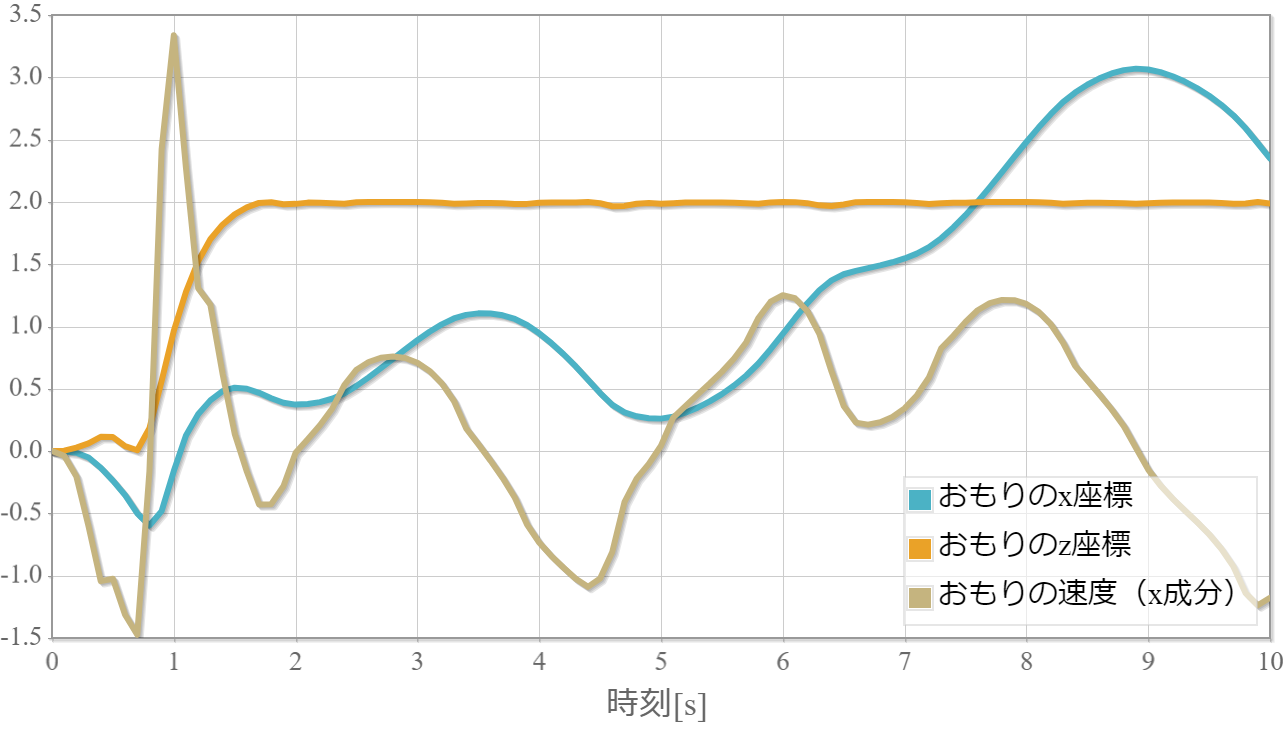
$k=5$の学習回数に対する成功確率

$k=5$の力学的エネルギーと振り子の位置の時系列データ

$k=10$の学習回数に対する成功確率

$k=10$の力学的エネルギーと振り子の位置の時系列データ

結果と考察とメモ

・最適行動評価関数を用いて問題なく学習ができたので、次回は最適行動評価関数にニューラルネットワークを用いた深層強化学習に取り組みます。
【メモ】減点に向かって収束させるにはどのような学習が必要なのか？
【メモ】３次元グラフィックスを作成する

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/20180728-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考（物理シミュレーション）

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。