シュレディンガー方程式に従う粒子の時間発展
２次元自由粒子

シュレディンガー方程式に従う粒子（電子を想定）の時間発展の様子を可視化することを目的に、様々な系におけるシミュレーションを行います。 前回シュレディンガー方程式に従う粒子の時間発展：自由粒子では、 １次元の場合のシミュレーション結果を取り扱ったので、今回は２次元自由粒子の場合を取り扱います。

平面波解の重ねあわせ

時間発展を追う上で取扱が容易な「ガウス分布」を取り扱います。 その場合、上式は次のようになります。

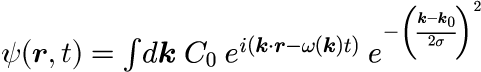
最後の因子が波数空間におけるガウス分布を表します。上式で「k_0」は中心となる波数で、粒子の平均の運動量と関係があります。 本節では、k_0 = 0 の場合と k_0 = 1.5 の場合について考えます（単位は下図を参照）。

k_0=0 の場合における2次元自由粒子の時間発展

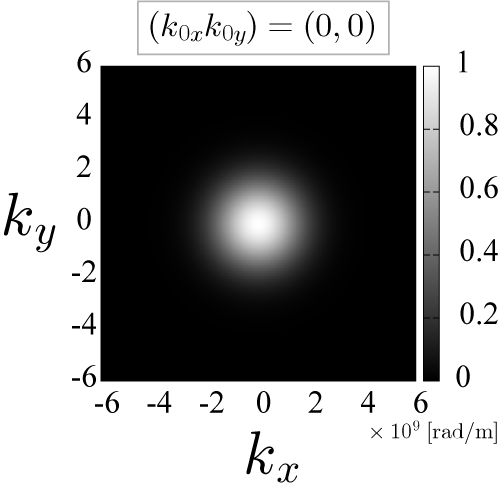
波数空間におけるガウス分布

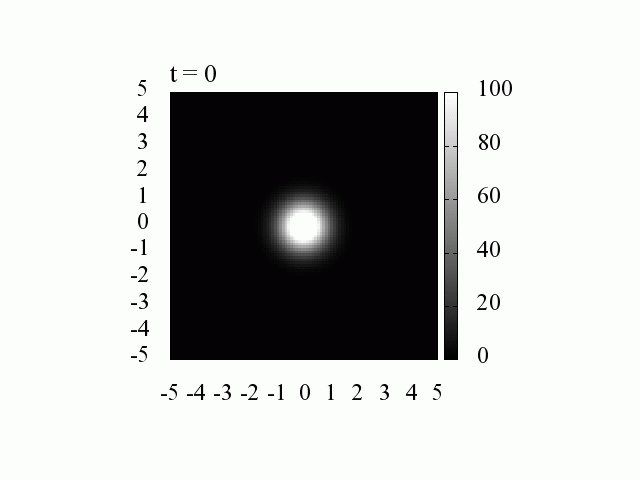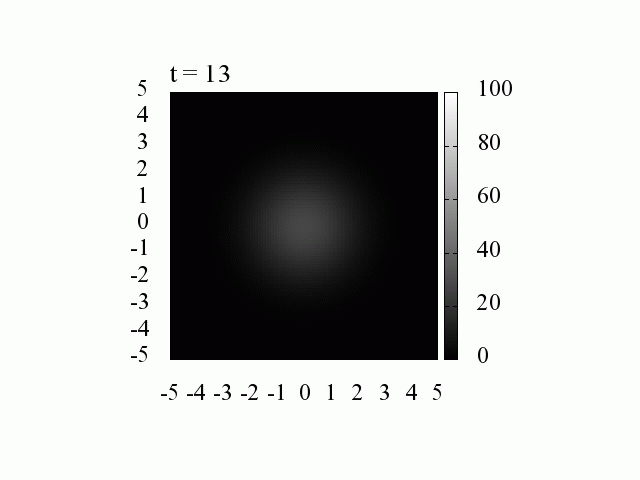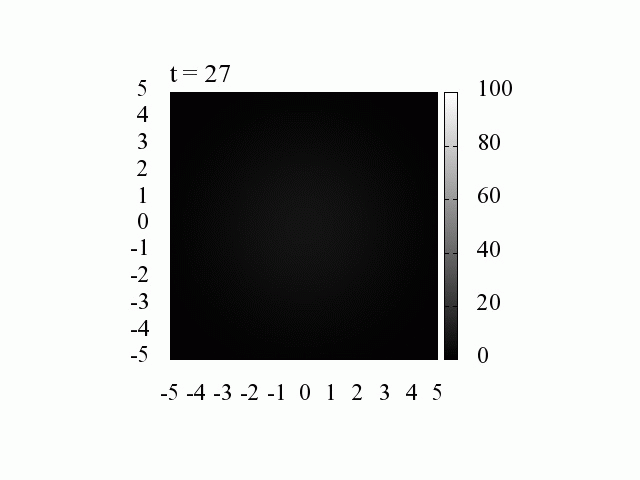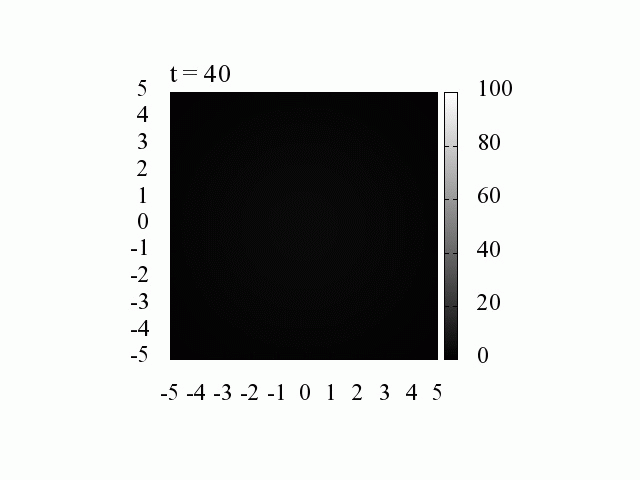
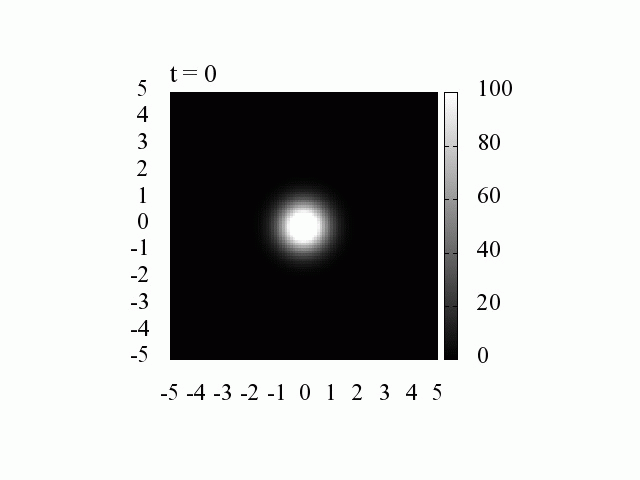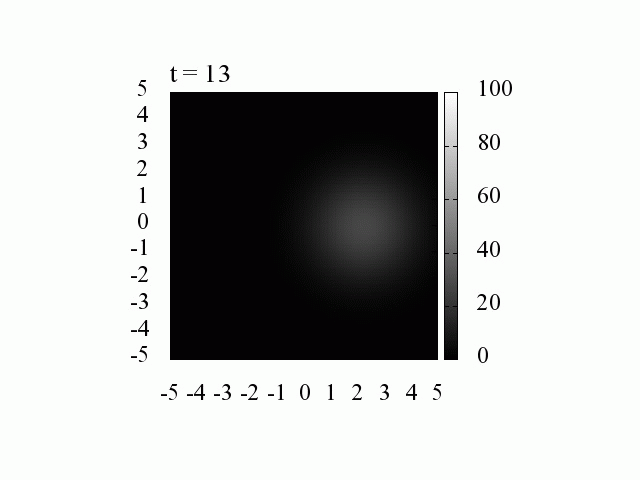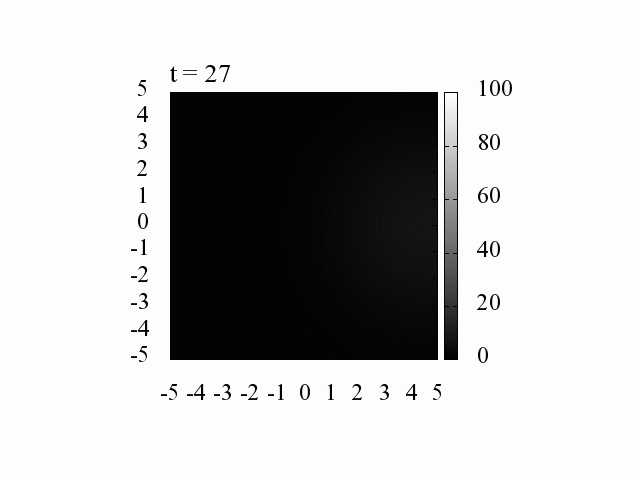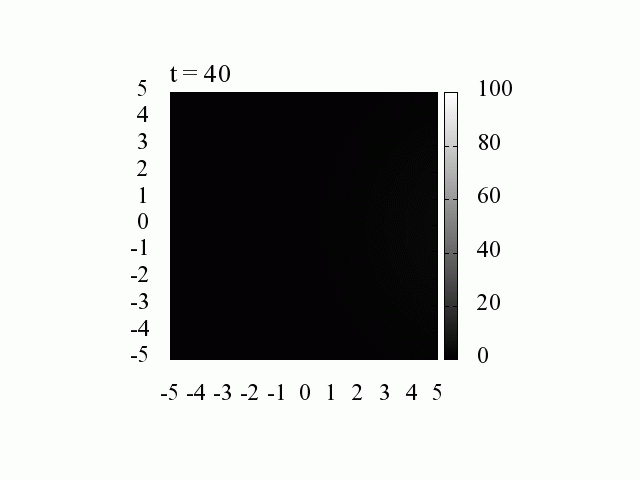
波動関数の時間発展(時間間隔 1[fs]=10^{-15}[s], 空間間隔 1[nm] =10^{-9}[m])

波数 k は様々な値を持つのでパルスは拡散していきます。 k_0=0 、つまり平均の運動量が０の場合には，中心は移動しません。 それにしても、電子はたった 20[fs]後には拡散してしまいます。

k_0=1.5 の場合における2次元自由粒子の時間発展

波数空間におけるガウス分布

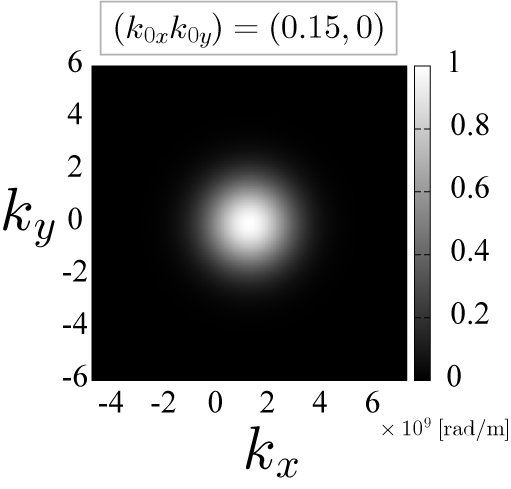
波動関数の時間発展(時間間隔 1[fs]=10^{-15}[s], 空間間隔 1[nm] =10^{-9}[m])

電子は k_0=1.5 に対応した平均の運動量を持ちます。 移動時ながら拡散していく様子が分かります。

VisualC++ ＋ gnuplotによるアニメーション

※不必要な変数、インクルードなどが多数ありますので、利用の際はご注意ください。
※VisualC++ から gnuplot を操作する方法をご参照ください。

#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <string>
#include <cstdio>
#include <iomanip>
#include <stdio.h>
#include <complex>
#include <sys/stat.h> // UNIXディレクトリ作成用
using namespace std;

double PI = acos(-1.0);
double e = 2.7182818284590452354;
complex<double> I = complex<double>(0.0,1.0);

const int N = 200 , Lx = 100, Ly = 100, Lz = 100;
complex<double> Psi = complex<double>(0.0,0.0) ;

const double c = 2.99792458E+8;
const double mu0 = 4.0*PI*1.0E-7;
const double epsilon0 = 1.0/(4.0*PI*c*c)*1.0E+7;
const double h  = 6.6260896 * 1.0E-34;
double hbar = h/(2.0*PI);
const double me = 9.10938215 * 1.0E-31;

int tn = 0 , t0 =0, te = 100;

double dz = 1.0E-10;
double dz_ = 1.0E-9;
double dk_ = 1.0/(dz_);
double dt = 1.0E-13/(double(te+1))  ,ts;
double dk = 1.2/(dz*double(N));
complex<double> k0x = 0.0;//0.15/dz; //<-----------------k0の指定
complex<double> k0y = 0.0;//0.15/dz; 
double sigma = sqrt(log(2.0))/(dz_);

string folder = "1", ff="", fg="";  //保存フォルダ名
ostringstream fname;

int main(){
	mkdir(folder.c_str(), S_IRWXU | S_IRWXG | S_IRWXO); // UNIX系のディレクトリ作成
	ff = folder + "/K.data";    ofstream fout_K( ff.c_str()); 

  complex<double> KK = complex<double>(0.0,0.0) ;

  for(tn=t0; tn<=te; tn++){
    double t = dt * double(tn) ;
    cout << tn << endl;

    ostringstream fname_Psi;
    fname_Psi <<  folder   + "/" << tn << ".data";//出力ファイル名
    string f_Psi = fname_Psi.str();
    ofstream fout_Psi;
    fout_Psi.open(f_Psi.c_str());

    for(int ix= -Lx/2; ix<= Lx/2; ix++){
      for(int iy= -Ly/2; iy<= Ly/2; iy++){
        Psi = complex<double>(0.0,0.0);
        double x = dz * ix;
        double y = dz * iy;
        for(int jx= -N/2; jx<= N/2 ; jx++){
          for(int jy= -N/2; jy<= N/2 ; jy++){
            complex<double> kx = k0x + dk*double(jx);
            complex<double> ky = k0y + dk*double(jy);
            double omega = hbar/(2.0*me) * (pow(abs(kx),2)+pow(abs(ky),2));
            if(ix==0 && iy==0 && tn==t0){
              KK = exp( -pow((kx-k0x)/(2.0*sigma),2) -pow((ky-k0y)/(2.0*sigma),2));
              fout_K << kx.real()/dk_  << " " << ky.real()/dk_  << " " << KK.real() << endl;
            }
            Psi += exp( I*(kx*x+ky*y - omega * t) -pow((kx-k0x)/(2.0*sigma),2) -pow((ky-k0y)/(2.0*sigma),2));
          }
          if(ix==0 && iy==0 && tn==t0){
            fout_K << "" << endl;
          }
        }
        Psi = Psi/ double(N);
        fout_Psi<< x/dz_  << " "<< y/dz_  << " " << pow(abs(Psi),2) << endl;
      }
      fout_Psi<< "" << endl;
    }
  }

	return 0;
}

gnuplotのテンプレート（colorMap.plt）

set terminal jpeg  enhanced font "Times" 20
set tics font 'Times,18'
set nokey
set size square
set rmargin 0
set lmargin 0

set pm3d
set pm3d map
set ticslevel 0
set cbrange[0:100]
set palette defined (0 "black",  100 "white")
set xrange[-5:5]
set yrange[-5:5]
set xtics -5, 1, 5
set ytics -5, 1, 5

if (exist("n")==0 || n<0) n=0      #変数の初期化
file0(n) = sprintf("2/%d.data",n)  #入力ファイル名
#file1(n) = sprintf("2/%d.data",n) #入力ファイル名
outfile(n) = sprintf("%d.jpg",n)   #出力ファイル名
title(n) = sprintf("t = %d",n)     #タイトル名

unset label 
set label title(n)  font 'Times,20'  at -5 , 5.5

set output outfile(n)

splot file0(n) with pm3d

if (n<40)  n=n+1; reread