１次元ガウシアンのスプライン補間を試す

スプライン補間とは、グラフ上の点を多項式を用いて曲線をでつなぐアルゴリズムで、 ３次関数を用いる３次スプライン補間が一般的です。 本稿では、次式で与えられる１次元ガウシアンを、与えられた１０点を用いてスプライン補間を行います。

(1)

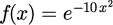
式(1)で与えられるガウシアンから１０点を用意し、この点を用いてスプライン補間を行います。

計算結果

赤線は式(1)の、青の四角は与えた１０点、 青線が与えた１０点を用いたスプライン補間。

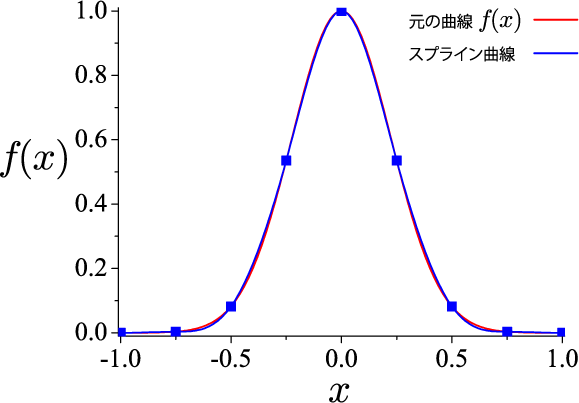
おおよそ、元のガウシアンと一致していることがわかります。

スプライン補間に関する参考ページ

■ ３次スプライン補間法（横田壽 氏）
■ 3 スプライン補間（山本昌志 氏）

C言語プログラムソース

中心アルゴリズムはpspline.c -- スプライン補間（Hidekazu Ito 氏）から拝借しております。

/*
１次元ガウス分布のスプライン補間
（2012.01.01）
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream>
#include <fstream>
using namespace std;

/***********************************************************
  pspline.c -- スプライン補間
  Hidekazu Ito 氏
  http://chaste.web.fc2.com/Reference.files/Algo.html
***********************************************************/
/* 周期関数用 */
#define  N  10
double xs[N + 1],
       ys[N + 1],
       zs[N + 1];

void maketable(double xs[], double ys[], double zs[])
{
  int i;
  double t;
  static double h[N + 1], d[N + 1], w[N + 1];

  for (i = 0; i < N; i++) {
    h[i] = xs[i + 1] - xs[i];
    w[i] = (ys[i + 1] - ys[i]) / h[i];
  }
  w[N] = w[0];
  for (i = 1; i < N; i++) d[i] = 2 * (xs[i + 1] - xs[i - 1]);
  d[N] = 2 * (h[N - 1] + h[0]);
  for (i = 1; i <= N; i++) zs[i] = w[i] - w[i - 1];
  w[1] = h[0];  w[N - 1] = h[N - 1];  w[N] = d[N];
  for (i = 2; i < N - 1; i++) w[i] = 0;
  for (i = 1; i < N; i++) {
    t = h[i] / d[i];
    zs[i + 1] = zs[i + 1] - zs[i] * t;
    d[i + 1] = d[i + 1] - h[i] * t;
    w[i + 1] = w[i + 1] - w[i] * t;
  }
  w[0] = w[N];  zs[0] = zs[N];
  for (i = N - 2; i >= 0; i--) {
    t = h[i] / d[i + 1];
    zs[i] = zs[i] - zs[i + 1] * t;
    w[i] = w[i] - w[i + 1] * t;
  }
  t = zs[0] / w[0];  zs[0] = t;  zs[N] = t;
  for (i = 1; i < N; i++)
    zs[i] = (zs[i] - w[i] * t) / d[i];
}

double spline(double t, double xs[], double ys[], double zs[])
{
  int i, j, k;
  double d, h, period;

  period = xs[N] - xs[0];
  while (t > xs[N]) t -= period;
  while (t < xs[0]) t += period;
  i = 0;  j = N;
  while (i < j) {
    k = (i + j) / 2;
    if (xs[k] < t) i = k + 1;  else j = k;
  }
  if (i > 0) i--;
  h = xs[i + 1] - xs[i];
  d = t - xs[i];
  return (((zs[i + 1] - zs[i]) * d / h + zs[i] * 3) * d
    + ((ys[i + 1] - ys[i]) / h
    - (zs[i] * 2 + zs[i + 1]) * h)) * d + ys[i];
}

int main(void)
{
  //１次元ガウシアン
  ofstream ofs( "Gaussian1.data" ); 
  for (int i=0; i<=N; i++)
  {
    xs[i] = -1.0 + 2.0 * double(i)/double(N);
    ys[i] = exp( -10.0 * pow(xs[i],2));
    ofs << xs[i] << " " << ys[i] << endl;
  }
  ofs.close();
  maketable(xs, ys, zs);
  ofstream ofs1_2( "Gaussian1_2.data" ); 
  for (double x = -1.0; x <= 1.0; x+=0.01)
  {
    ofs1_2 << x << " " << exp( -10.0 * pow(x,2)) << " " << spline(x, xs, ys, zs) << endl;
  }
  ofs1_2.close();
}