HTML5による物理シミュレーション環境の構築 ~WebGLライブラリThree.js 入門(2/3)~
本稿では新しいWEBページ用の言語であるHTML5+WebGLを利用して、 ウェブブラウザ上で、物理シミュレーションの計算と描画をリアルタイムに実行する「物理シミュレータ」の作成までの手順を記述します。 本稿では、物理シミュレータの例として、任意の初期条件に対する2重振り子の時間発展を4次のルンゲクッタ法を計算する「2重振子シミュレータ」を構築します。また、本稿では WebGL を簡単に利用することができるWebGLライブラリとして著名な Three.js を用いています。 物理や工学とは無関係に、初めて Three.js を利用する人がチュートリアルとしても利用できることも意図しております。 パート1では、主に Three.js の使い方について触れました。 パート2では、拘束力のある運動の代表例である単振子を取り上げ、物理演算結果のリアルタイム描画+物理量の時間発展の様子をグラフ化します。 (※)グラフ描画はflotr2 というJavascriptライブラリを利用します。
目次
パート1 (すべて表示)
パート2
- 仮想物理実験室の構築
- 支柱・おもり・ひもの描画
- ニュートンの運動方程式
- 微分方程式の数値解計算アルゴリズム(4次のルンゲクッタ法)の実装
- インターフェースの実装(物理量の出力とボタンと設置)
- グラフの描画(Javascript ライブラリ flotr2 の使い方)
- 物理量のリアルタイムグラフ描画
- おまけ
パート3 (すべて表示)
仮想物理実験室の構築
仮想物理実験室となる以下のような3次元空間を WebGLのJavascript ライブラリである Three.jsを利用して準備します。
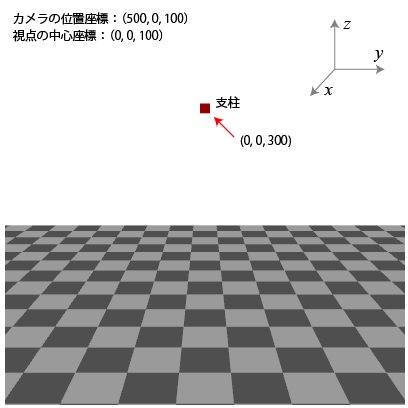
Three.jsにて2重振り子シミュレータを作成する上で必要な物体は、
(1) 支柱を表す直方体 → 5.立方体の宣言とシーンへの追加
(2) 床を表す平面 → 少しだけ応用(平面と球の追加)
(3) 振り子のおもりを表す球 → 少しだけ応用(平面と球の追加)
(4) 振り子のひもを表す線 → 未学習
です。この物体の追加は
- 0.キャンバスの額縁の準備
- 1.Three.js の初期化(initThree())
- 2.カメラの準備(initCamera())
- 3.シーンの準備(initScene())
- 4.光源の準備(initLight())
- 5.物体の準備(initObject())
- 6.レンダリングの実行(threeStart())
の5番目(物体の準備)の関数に追加します。
床の描画
仮想物理実験室の市松模様の床となる平面を描画します。 平面の描画はパート1の少しだけ応用(平面と球の追加)で実装したとおりですが、 2種類の色のサイズ50の正方形を縦横21×21個交互に配置します。
//床の描画
var n_yuka = 10, yuka_w = 50;
for(var i=-n_yuka; i<=n_yuka ; i++){
for(var j=-n_yuka; j<=n_yuka ; j++){
if((i+j)%2==0) var plane = new THREE.Mesh(
new THREE.PlaneGeometry(yuka_w, yuka_w, 1, 1),
new THREE.MeshLambertMaterial({color: 0x999999}));
else var plane = new THREE.Mesh(
new THREE.PlaneGeometry(yuka_w, yuka_w, 1, 1),
new THREE.MeshLambertMaterial({color: 0x4d4d4d}));
plane.position.x = j*yuka_w;
plane.position.y = i*yuka_w;
plane.receiveShadow = true;
scene.add(plane);
}
}
ただし、「n_yuka」と「yuka_w」は縦と横の個数と正方形の一辺の大きさです。
サンプル4:tutorial4.html(仮想物理実験室)
仮想物理実験室の市松模様の床+カメラ位置の移動(マウスドラック、ホイール)を実装しています。
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>Three.js チュートリアル4:仮想物理実験室</title>
<script src="Three.js"></script>
<style>
div#canvas-frame{
border: none;
cursor: pointer;
width: 400px;
height: 400px;
background-color: #FFFFFF;
}
</style>
<script>
var width, height;
var renderer;
function initThree() {
width = document.getElementById('canvas-frame').clientWidth;
height = document.getElementById('canvas-frame').clientHeight;
renderer = new THREE.WebGLRenderer({antialias: true});
renderer.setSize(width, height);
document.getElementById('canvas-frame').appendChild(renderer.domElement);
renderer.setClearColorHex(0xFFFFFF, 1.0);
renderer.shadowMapEnabled = true;//影をつける(1)
}
var camera;
function initCamera() {
camera = new THREE.PerspectiveCamera( 45 , width / height , 1 , 10000 );
camera.up.x = 0;
camera.up.y = 0;
camera.up.z = 1;
camera.position.set(500,0, 100);
}
var scene;
function initScene() {
scene = new THREE.Scene();
}
var light, light2;
function initLight() {
light = new THREE.DirectionalLight(0xFFFFFF, 1.0, 0);
light.position.set( 20, 20, 1000 );
light.castShadow = true;
scene.add(light);
light2 = new THREE.AmbientLight(0x777777);
scene.add(light2);
}
var plane;
function initObject(){
//床の描画
var yuka_n = 10, yuka_w = 50;//床の個数とサイズ
for(var i=-yuka_n; i<=yuka_n ; i++){
for(var j=-yuka_n; j<=yuka_n ; j++){
if((i+j)%2==0) var plane = new THREE.Mesh(
new THREE.PlaneGeometry(yuka_w, yuka_w, 1, 1),
new THREE.MeshLambertMaterial({color: 0x999999}));
else var plane = new THREE.Mesh(
new THREE.PlaneGeometry(yuka_w, yuka_w, 1, 1),
new THREE.MeshLambertMaterial({color: 0x4d4d4d}));
plane.position.x = j*yuka_w;
plane.position.y = i*yuka_w;
plane.receiveShadow = true;
scene.add(plane);
}
}
}
function loop() {
camera.lookAt( {x:0, y:0, z:100 } );
renderer.clear();
renderer.render(scene, camera);
window.requestAnimationFrame(loop);
}
var down = false;
var sy = 0, sz = 0;
window.onmousedown = function (ev){ //マウスダウン
if (ev.target == renderer.domElement) {
down = true;
sy = ev.clientX; sz = ev.clientY;
}
};
window.onmouseup = function(){ //マウスアップ
down = false;
};
window.onmousemove = function(ev) { //マウスムーブ
var speed = 2;
if (down) {
if (ev.target == renderer.domElement) {
var dy = -(ev.clientX - sy);
var dz = -(ev.clientY - sz);
camera.position.y += dy*speed;
camera.position.z -= dz*speed;
sy -= dy;
sz -= dz;
}
}
}
window.onmousewheel = function(ev){//マウスホイール
var speed = 0.2;
camera.position.x += ev.wheelDelta * speed ;
}
function threeStart() {
initThree();
initCamera();
initScene();
initLight();
initObject();
loop();
}
</script>
</head>
<body onload="threeStart();">
<div id="errer"></div>
<div id="canvas-frame"></div>
</body>
</html>
実行結果
マウスドラックで視点を移動することができます
(※マウスホイールも実装していますが、ウィンドウスクロールしてしまうため確認できません。)
支柱・おもり・ひもの描画
2重振り子を構成する、支柱、おもり、ひもを直方体、球、直線をそれぞれ用いて表現します。 その際に支柱や球をわかりやすく管理するために、それぞれ「クラス」を定義し、位置座標などをクラスのプロパティとして利用することにします。
Javascript におけるクラス
Javascript にてクラスの定義とクラスのインスタンスである「オブジェクト」の宣言は次のとおりです。
var クラス名 = function(a,b,c){ //クラスの定義
this.プロパティ名1 = a;
this.プロパティ名2 = b;
this.プロパティ名3 = c;
}
var オブジェクト名 = new クラス名 (x, y, z); //オブジェクトの宣言
クラスと言いましたが、Javascript では C++言語のような厳格な定義はありません。 上記のプロパティは、隠蔽化されているわけではなく構造体と同様に「オブジェクト名.プロパティ名」でプロパティへはで参照することができます(Javascript でもプロパティを隠蔽する方法があります)。また、クラスのメソッドは
クラス名.prototype.メソッド名 = function(引数){
(関数の実行内容)
}
で定義します。 定義したメソッドを呼び出すためには、
オブジェクト名.メソッド名(引数)
ただし、本節ではクラスを構成する重要な要素である「メソッド」は利用しないため、実質的には構造体と同じです。
PollクラスとBallクラスの定義とオブジェクトの宣言
支柱(直方体)とおもり(球)のクラスの定義とオブジェクトの宣言を行います。
それぞれのプロパティとして、空間位置座標(x,y,z)を設定します。
(1)L(ひもの長さ)を宣言
(2)支柱のクラス Pollを定義
(3)pollオブジェクトの宣言と初期化
(4)おもりのクラス Ballを定義
(5)pollオブジェクトの宣言と初期化
var L = 200; //(1)
var Poll = function(x,y,z){ //(2)
this.x = x; this.y = y; this.z = z;
};
var poll = new Poll(0,0,300); //(3)
var Ball = function(x,y,z){ //(4)
this.x = x; this.y = y; this.z = z;
};
var ball = new Ball(0,L,poll.z); //(5)
ひもの描画(直線)
Three.js にて直線を描画するには、予め頂点の位置座標を「Geometry」クラスのオブジェクトに配列化しておく必要があります。
支柱とおもりをつなぐ直線を描画する手順は、
(1)「Geometry」クラスのオブジェクト「geometry」を宣言
(2)「geometry」の頂点プロパティ(vertices)に支柱の位置座標を頂点として追加
(3)「geometry」の頂点プロパティ(vertices)におもりの位置座標を頂点として追加
(4)「Line」クラスのオブジェクト「line」を宣言
(5)「line」をシーンに追加
です。具体的には
var geometry = new THREE.Geometry(); //(1)
geometry.vertices.push( new THREE.Vertex( new THREE.Vector3( poll.x, poll.y, poll.z) ) ); //(2)
geometry.vertices.push( new THREE.Vertex( new THREE.Vector3( ball.x, ball.y, ball.z) ) ); //(3)
var line = new THREE.Line( geometry, new THREE.LineBasicMaterial( { color: "0x000000", linewidth: 1} ) ); //(4)
scene.add( line ); //(5)
と記述します。
実行結果
マウスドラックで視点を移動することができます
(※マウスホイールも実装していますが、ウィンドウスクロールしてしまうため確認できません。)
支柱、おもり、ひもの描画が無事に終了しました。 しかしまだ当然動きません。 次節では、このおもりを動かすためのアルゴリズムを加えます。
ニュートンの運動方程式
ニュートンの運動方程式とは?
物体の運動の時間発展は「ニュートンの運動方程式」と呼ばれる方程式で決定されることが知られています。 ニュートンの運動方程式とは
(1)「力」が加えられた物体は、力の加わった方向に「加速」する
(2)「力」が大きいほど「加速」は大きくなる
(3)「加速」の大きさは質量に反比例する
で表現することができ、日常生活でも直感的に正しいと感じられます。 これを模式的に表したのが下の図です。

これを式で表すと
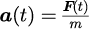
となり、これはニュートンの運動方程式と呼ばれます。上式の「t」は時間(単位は[s(秒)])を表し、加速度と力は時間に依存することを明示的に表しています。ただし、力と加速度
は、大きさと方向を持つ「ベクトル」です。
この式は、ある時刻 t の物体に加わる力がわかれば、その瞬間の加速度が得られることを意味します。
また、物体の加速度は位置の2回微分で定義されるので、
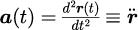
と表すことができます。
つまり、加速度を2回積分することで、物体の位置を計算することができることになります。
単振子の運動方程式
単振子とは、支柱に伸び縮みしない重さを無視することができるひもつながれたおもりのことです。 単振子のおもりには、地球がおもりを引く力「重力」と糸がおもりを引く力「張力」の2つが加わっています。 単振子に対する運動方程式を解くことで、単振子の時間発展を計算することができます。
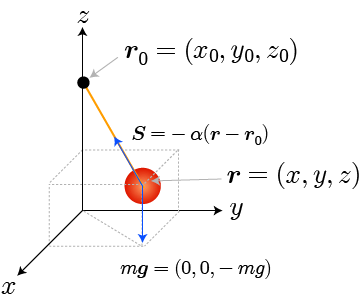
上の図で、が張力、
が重力となります。
この式より、単振り子の運動方程式は
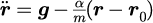
となります。
ここで問題なのが、重力は地上では一定値で既知であるのに対して、張力は方向は既知であるが大きさは未知であることです。つまり、「」はその他の条件から決める必要があります。
それは、紐の長さが伸び縮みしないという拘束条件です。
詳細は「ラグランジュ未定乗数法を用いた球面振子のシミュレーション」に記載していますが、
は
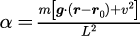
となり、単振り子の運動方程式は
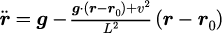
と決まります。この式を何らかの方法で解くことで、物体の時間発展を計算することができます。
【物理に少し詳しい方向け説明】
一般に単振子の解析には極座標を用いますが、極座標表記では張力を計算することができません。本稿の手法は、張力を得るためにラグランジュ未定乗数法を用いています。
微分方程式の数値解計算アルゴリズム(4次のルンゲクッタ法)の実装
そもそも数値計算とは?
物体の運動を記述する微分方程式は、特別な系(条件)の場合以外は解析的に解くことができません。 「解析的に解く」とは、方程式の解を導くことで、学校(小中高)では解析的に解ける問題しか扱っていません。 では、解析的に解けない方程式はどうするのかというと、コンピュータを用いて数値的に解くことになります。 また、数値的に解くための手順(手段)を計算アルゴリズムと呼びます。 一般に、「コンピュータ・シミュレーション」とは解析的に解くことのできない物理現象を、数値的に解くことで理解することを指します。 本稿の目的である「2重振り子シミュレータ」も解析的には解くことができないため、数値的に解きながら計算結果を描画することを行なっています。
数値計算の重要性はコンピュータの性能向上に伴い、どんどん増してきています。 実際の「もの」を作らなくても、コンピュータ上に創った仮想世界の中でシミュレートすることでおおよその特性を知ることができるので、コンピュータの性能向上は科学・技術分野における生産性の向上に直接寄与します。つまり、産業分野おける競争力の原資となるわけです。
計算アルゴリズムと計算精度
与えられた方程式をコンピュータを用いて数値的に解く場合、有限の桁数で計算するため、精度も有限となります。 真の値からのズレは計算誤差と呼ばれ、誤差が大きくなると見た目にも物理的にはあり得ない挙動を示すことになるため、実用上十分な計算精度が必要となります。計算精度を決めるのは計算アルゴリズムです(ちなみに解析解の精度は無限です)。 アルゴリズムは精度が良いほど良いわけではなく、計算コストや汎用性を考慮する必要があります。 一般にアルゴリズムの精度と使いやすさはトレードオフの関係にあると考えて間違いありません。
式(5)のような微分方程式を数値的に解く方法として最も一般的なのは、空間ないし時間を微小領域に分けて(差分化)逐次数値的に解く方法です。 最も単純なのはオイラー法と呼ばれる精度が1次のアルゴリズムです(精度については後述します)。一般にオイラー法を用いた数値計算は精度が悪く、すぐに発散してしまいます。 オイラー法に比べて、実用的な計算の精度と速度を兼ね備えかつ汎用性の高いアルゴリズムとして知られているのが4次のルンゲクッタ法 です。1900年ごろにルンゲ氏とクッタ氏によって開発された本手法は、4次の精度です。
精度の次数
オイラー法にせよ、ルンゲクッタ法にせよ、微分方程式の差分の大きさ h を小さくするほど精度が良くなりますが、その分だけ計算回数(計算時間)が増えることになります。計算アルゴリズムにはアルゴリズムの導出過程における近似に由来する精度が存在します。 アルゴリズムの精度は、計算アルゴリズムから得られる数値解が、真の解のテーラー展開と比較して第何項目まで一致するかで表現し、 この項数のこと次数と言います。 つまり、オイラー法は1次の精度なので、テーラー展開の1次までは真の解と一致するのに対して、ルンゲクッタ法は4次の精度なのでテーラー展開の4次までは真の解と一致することを保証しています。 一見、1次と4次では大した差が内容に思えます。 本稿で計算する2重振り子の時間間隔は 0.001 と設定しているですが、単位時間に対してオイラー法では 0.001 程度の誤差に対して、ルンゲクッタは 0.001の4乗、0.000000000001 程度の精度となり計算精度は圧倒的に良くなります。
Javascript におけるルンゲクッタ法の実装
本節ではルンゲクッタ法による時間発展の計算をBallクラスのメソッドとして実装します。 具体的な実装は次のステップで行います。(0)時間、時間間隔、1フレームあたりの計算回数の設定
(1)Ballクラスのプロパティに速度を追加
(2)Ballクラスのメソッドにルンゲクッタ法による計算アルゴリズムを追加
(3)「loop()」関数内で、上記メソッドを呼び出す
(0)時間、時間間隔、1フレームあたりの計算回数の設定
「時間」と「時間間隔」とは、仮想物理実験室内の「時間」とアルゴリズムで計算する際の「時間間隔」を指します。 つまり、仮想物理実験室において「時間」=「時間間隔×計算回数」となるわけです。 先にも述べましたが、時間間隔が小さいほど計算精度が良くなりますが、その分だけ計算回数に対する「時間」の進み方は遅くなります。 「window.requestAnimationFrame」関数を用いたアニメーションの場合、標準では1秒あたり60回(60fps)計算(描画)を行うため、「時間間隔」を小さくするほど動きはスローになってしまします。 一方、時間間隔を大きくすると動きは早くなりますが、計算精度はガタ落ちになります。 計算精度を上げつつ(時間間隔を小さくしつつ)、動きを早くしたいときに一般に行われるのが、描画の間引きで、1回の描画の度に複数回計算させればよいだけです。
var t = 0; //時刻 var dt = 0.001; //時間刻み var skip = 500; //1フレームあたりの計算回数
仮想物理実験室内の時間は、1フレームあたり 0.001[s/回]×500[回] = 0.5[s] 進むことになります。 もし、コンピュータの計算速度が十分であれば1秒あたり60回描画されるので、現実の世界1秒に対して、仮想物理実験室では30秒の時間がすぎることになります。もちろん1フレームあたりの計算回数を大きくし過ぎると、計算が追いつかずにフレームレートが下がり、カクカクとした動きになってしまいます。
(1)Ballクラスのプロパティを追加
ルンゲクッタ法を用いる場合、おもりの速度も必要になるのでプロパティに速度も追加しておきます。
var Ball = function(x,y,z,vx,vy,vz){
this.x = x; this.y = y; this.z = z;
this.vx = vx; this.vy = vy; this.vz = vz;
};
var ball = new Ball(0, L, 300, 0, 0, 0);
(2)4次のルンゲクッタをBallクラスのメソッドとして追加
おもりの運動を計算するアルゴリズムをBallクラスのメソッドとして実装します。 Javascriptにてクラスのメソッドの定義は「クラス名.prototype.メソッド名」で行うことは先にも述べました。4次のルンゲクッタ法によるアルゴリズムをJavascript でコーディングした結果が次のとおりです。
Ball.prototype.fx = function(t, x, y, z, vx, vy, vz){
return vx;
}
Ball.prototype.fvx = function(t, x, y, z, vx, vy, vz){
var l2 = Math.pow(x,2) + Math.pow(y,2) + Math.pow(z,2);
var v2 = Math.pow(vx,2) + Math.pow(vy,2) + Math.pow(vz,2);
return (g*z-v2) * x / l2 ;
}
Ball.prototype.fy = function(t, x, y, z, vx, vy, vz){
return vy;
}
Ball.prototype.fvy = function(t, x, y, z, vx, vy, vz){
var l2 = Math.pow(x,2) + Math.pow(y,2) + Math.pow(z,2);
var v2 = Math.pow(vx,2) + Math.pow(vy,2) + Math.pow(vz,2);
return (g*z-v2) * y / l2 ;
}
Ball.prototype.fz = function(t, x, y, z, vx, vy, vz){
return vz;
}
Ball.prototype.fvz = function(t, x, y, z, vx, vy, vz){
var l2 = Math.pow(x,2) + Math.pow(y,2) + Math.pow(z,2);
var v2 = Math.pow(vx,2) + Math.pow(vy,2) + Math.pow(vz,2);
return -g + (g*z-v2) * z / l2 ;
}
Ball.prototype.RungeKutta4 = function(){
var k1 = new Array(6);
var k2 = new Array(6);
var k3 = new Array(6);
var k4 = new Array(6);
var x = this.x - poll.x;
var y = this.y - poll.y;
var z = this.z - poll.z;
var vx = this.vx;
var vy = this.vy;
var vz = this.vz;
k1[0]=dt*this.fx(t,x,y,z,vx,vy,vz);
k1[1]=dt*this.fvx(t,x,y,z,vx,vy,vz);
k1[2]=dt*this.fy(t,x,y,z,vx,vy,vz);
k1[3]=dt*this.fvy(t,x,y,z,vx,vy,vz);
k1[4]=dt*this.fz(t,x,y,z,vx,vy,vz);
k1[5]=dt*this.fvz(t,x,y,z,vx,vy,vz);
k2[0]=dt*this.fx(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k2[1]=dt*this.fvx(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k2[2]=dt*this.fy(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k2[3]=dt*this.fvy(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k2[4]=dt*this.fz(t+dt/2.0, x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k2[5]=dt*this.fvz(t+dt/2.0,x+k1[0]/2.0,y+k1[2]/2.0,z+k1[4]/2.0,vx+k1[1]/2.0,vy+k1[3]/2.0,vz+k1[5]/2.0);
k3[0]=dt*this.fx(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k3[1]=dt*this.fvx(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k3[2]=dt*this.fy(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k3[3]=dt*this.fvy(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k3[4]=dt*this.fz(t+dt/2.0, x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k3[5]=dt*this.fvz(t+dt/2.0,x+k2[0]/2.0,y+k2[2]/2.0,z+k2[4]/2.0,vx+k2[1]/2.0,vy+k2[3]/2.0,vz+k2[5]/2.0);
k4[0]=dt*this.fx(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
k4[1]=dt*this.fvx(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
k4[2]=dt*this.fy(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
k4[3]=dt*this.fvy(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
k4[4]=dt*this.fz(t+dt/2.0, x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
k4[5]=dt*this.fvz(t+dt/2.0,x+k3[0],y+k3[2],z+k3[4],vx+k3[1],vy+k3[3],vz+k3[5]);
this.x += (k1[0]+2.0*k2[0]+2.0*k3[0]+k4[0])/6.0;
this.vx += (k1[1]+2.0*k2[1]+2.0*k3[1]+k4[1])/6.0;
this.y += (k1[2]+2.0*k2[2]+2.0*k3[2]+k4[2])/6.0;
this.vy += (k1[3]+2.0*k2[3]+2.0*k3[3]+k4[3])/6.0;
this.z += (k1[4]+2.0*k2[4]+2.0*k3[4]+k4[4])/6.0;
this.vz += (k1[5]+2.0*k2[5]+2.0*k3[5]+k4[5])/6.0;
}
ルンゲクッタ法は非常に汎用性が高く、一般的な微分方程式で適用可能です。 上記の
Ball.prototype.fx = function(t, x, y, z, vx, vy, vz){}
Ball.prototype.fvx = function(t, x, y, z, vx, vy, vz){}
Ball.prototype.fy = function(t, x, y, z, vx, vy, vz){}
Ball.prototype.fvy = function(t, x, y, z, vx, vy, vz){}
Ball.prototype.fz = function(t, x, y, z, vx, vy, vz){}
Ball.prototype.fvz = function(t, x, y, z, vx, vy, vz){}
の関数の中身を微分方程式で与えられる項とするだけです。一度使い方を覚えると応用範囲は非常に広いです。
(3)「loop()」関数内で、上記メソッドを呼び出す
計算アルゴリズムをクラスのメソッドとして定義しただけでは、当たり前ですがまだ動きません。 具体的にメソッドを呼び出す必要があります。 もちろん計算結果を描画してアニメーションしたいわけなので、「loop()」関数内でメソッドを呼び出す必要があります。 「loop()」関数は、処理落ちがなければ1秒あたり60回呼び出されるわけですが、その際に「skip」で指定した回数だけメソッドを呼び出します。
function loop() {
for(var i=1; i<=skip; i++ ) ball.RungeKutta4();
t += dt * skip;
(省略)
}
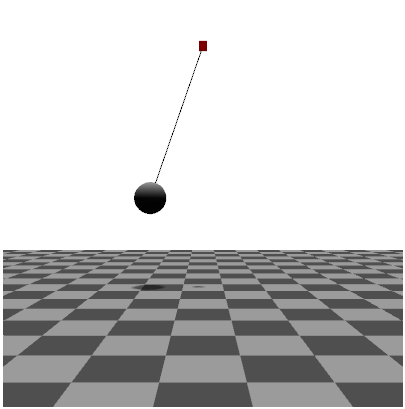
実行結果
以下の図は実行画面のキャプチャです。実際の実行画面は「サンプル4-2」をご覧下さい。
以下はデモページのキャプチャ画象です → デモページへ
インターフェースの実装(物理量の出力とボタンと設置)
ここから、Three.jsの使い方に戻ります。 仮想物理実験室でシミュレートする目的の一つは、おもりの位置や張力などの物理量の時間変化を調べることです。 本節では単純に計算結果を画面に描画するプログラムをJavascriptで実装します。 また、HTMLファイルを読み込んだ直後にスタートするのでは使い勝手が悪いので、 「スタート」ボタン「ストップ」ボタン、さらには「リセット」ボタンを作成します。
Javascript によるHTML文書の書き換え
Javascript を利用することで動的にHTML文書を書き換えることができます。
そのためには、Document Object Model(以下、DOM)と呼ばれる仕組みを理解する必要があります。
DOM とはHTML文書やXML文書の中身を Javascript などで操作するためのAPIで、いろいろなことができます。
本稿では、各時刻における球の座標、球の速度、ひもの長さ、ひもの張力、最大張力を DOM を用いて、次のステップで出力します。
(1)HTML の body 要素に出力先の要素を追加
(2)HTMLに出力するクラスメソッドを宣言
(3)張力を計算するクラスメソッドを宣言
(4)CSS を style 要素に追加
(1)HTML の body 要素に出力先の要素を追加
HTML の body 要素に出力先として、id名を設定した span 要素を追加します。
<div id="status">
<h2>ステータス<button onclick="startPauseButton();" id="startPauseButton">スタート</button><button onclick="resetButton();">リセット</button></h2>
<table>
<tr>
<td>時刻[s]</td><td><span id="ft"></span></td>
</tr>
<tr>
<td>球の座標[m]<br />(x,y,z)</td><td><span id="fx"></span> <span id="fy"></span> <span id="fz"></span></td>
</tr>
<tr>
<td>球の速度[m/s]<br />(vx,vy,vz)</td><td><span id="fvx"></span> <span id="fvy"></span> <span id="fvz"></span></td>
</tr>
<tr>
<td>ひもの長さ[m]</td><td><span id="fL"></span></td>
</tr>
<tr>
<td>ひもの張力[N]</td><td><span id="ftension"></span></td>
</tr>
<tr>
<td>最大張力[N]</td><td><span id="ftension_max"></span></td>
</tr>
</table>
</div>
(2)HTMLに出力するクラスメソッドを宣言
id名で指定した要素の中身に Javascript で出力します。 その際にDOMの仕組みを理解する必要があります。 id名で指定した要素の中身に文字列を出力するには、Javascript で次のようにコーディングします。
document.getElementById("id名").innerHTML = 文字列
上記の「document」はHTML文書を指します。 次の「getElementById("id名")」はid名で指定した要素を指し、「innerHTML」は要素の中身を指します。 つまり、上の例は「HTML文書の中のid名で指定された要素の中身」を「文字列」とするという意味です。 先に用意した span 要素に出力するための関数を、Ballクラスのメソッドとして用意します。
Ball.prototype.write = function(){
document.getElementById("fx").innerHTML = (this.x).toFixed(1);
document.getElementById("fy").innerHTML = (this.y).toFixed(1);
document.getElementById("fz").innerHTML = (this.z).toFixed(1);
document.getElementById("fvx").innerHTML = (this.vx).toFixed(1);
document.getElementById("fvy").innerHTML = (this.vy).toFixed(1);
document.getElementById("fvz").innerHTML = (this.vz).toFixed(1);
var L = Math.sqrt( Math.pow(this.x-poll.x,2) + Math.pow(this.y-poll.y,2) + Math.pow(this.z-poll.z,2) );
document.getElementById("fL").innerHTML = (L).toFixed(4);
document.getElementById("ftension").innerHTML = Math.abs(this.tension()).toFixed(2);
document.getElementById("ftension_max").innerHTML = (tension_max).toFixed(2);
document.getElementById("ft").innerHTML = (t).toFixed(1);
}
ただし、「this」は宣言したオブジェクト自身を指し、「this.x」は自分自身のプロパティを参照しています。 また、「.toFixed(1)」は小数以下の桁数を指定するためのNumberクラスのメソッド、 「this.tension()」は次で定義する張力を計算するBallクラスのメソッドです。
(3)張力を計算するクラスメソッドを宣言
張力は、単振子の運動方程式を示した際の「」から得られます。
「
」は式(4)で示しているので、張力の計算を Javascript で次のように実装します。
Ball.prototype.tension = function() {
var L = Math.sqrt(Math.pow(this.x,2) + Math.pow(this.y,2) + Math.pow(this.z,2));
var v2 = Math.pow(this.vx,2) + Math.pow(this.vy,2) + Math.pow(this.vz,2);
var tension = (this.m * (-g*(this.z-poll.z)+v2) )/L; //張力
if(tension_max < Math.max(tension)) tension_max = tension; (1)
return tension;
}
張力の最大値を「tension_max」と表し、もし「tension_max」よりも大きな「tension」が加わった時に、 「tension_max」の値を更新しています。
(4)CSS を style 要素に追加
最後に、見栄えを整えるための CSS を style 要素に追加します。 CSSは head 要素のなかの style 要素の中に記述します。
div#status *{
font-size:small;
}
div#status{
float:left;
width:200px;
background-color: #EEEEEE;
}
ボタンの設置とイベントの追加
ボタンは HTML の「button」要素で簡単に実現することができます。 さらにイベント属性のの一つである「onclick」を設定することで、クリック時に実行する Javascriptの関数を指定することができます。
<button onclick="startPauseButton();" id="startPauseButton">スタート</button> <button onclick="resetButton();">リセット</button>
上記のうちスタートボタンには id名が設定されています。 これは、ボタン要素の中身を状態によって書き換えることを意図しています。 つまり、実行プログラムの状態を「ポーズ」と「実行中」の2つとし、状態が「実行中」のときはボタン要素の中身を「ストップ」とし、状態が「ポーズ」のときはボタン要素の中身を「スタート」します。
function startPauseButton(){
if(!pause) pause = true;
else pause = false;
}
function resetButton(){
t=0;
ball.x = 0;
ball.y = L;
ball.z = poll.z;
ball.vx = 0;
ball.vy = 0;
ball.vz = 0;
}
張力により糸の色を変化させる
最後に、張力の大きさによってひもの色を変化させます。 張力が最大張力の場合に赤色、張力が0の場合に白色となるように指定します。 ひもの色は「loop()」関数の中で直線を描画する「Line」クラスのオブジェクト「line」を宣言時に、「color」プロパティを16進数で指定することで設定できます。具体的には次のように記述します。
//2点間の線を引く
var geometry = new THREE.Geometry();
geometry.vertices.push( new THREE.Vertex( new THREE.Vector3( poll.x, poll.y, poll.z) ) );
geometry.vertices.push( new THREE.Vertex( new THREE.Vector3( ball.x, ball.y, ball.z) ) );
var rr = parseInt(ball.tension()/tension_max * 16).toString(16) + parseInt(ball.tension()/tension_max * 16).toString(16); //(1)
var line = new THREE.Line( geometry, new THREE.LineBasicMaterial( { color: "0x" + rr + "0000" } ) ); //(2)
scene.add( line );//シーンに追加
上記の(1)は、赤色の大きさを決めるために「張力/最大張力」を計算し、16段階(0,1,2,~9,A~F)で表現します。 (1)で得られた16進数を用いて「color」プロパティを(2)で設定します。
実行結果
以下の図は実行画面のキャプチャです。実際の実行画面は「サンプル4-3」をご覧下さい。
以下はデモページのキャプチャ画象です → デモページへ

グラフの描画(Javascript ライブラリ flotr2 の使い方)
前節では物理量をリアルタイムに表示しましたが、やはり物理シミュレータとしては、グラフがほしいところです。 本節では、Javascript 用のグラフライブラリflotr2を利用して、 物理量の時間発展をリアルタイムにグラフ描画することを行います。 Three.js と組み合わせて利用する場合、個人的には flotr2 が一番使いやすかったです。
flotr2 のダウンロード
flotr2 のダウンロードは、「https://github.com/HumbleSoftware/Flotr2」にアクセスし、下図の「ZIP」をクリックして全ファイルをダウンロードします。 flotr2 を使用する際には「flotr2.min.js」だけで十分ですが、サンプルも同包されているので、暇な時に見てみるとインスピレーションが湧いてくることと思います。
「Three.js」と同じフォルダにコピーしてください。これで準備完了です。
flotr2 の動作確認
次のプログラムソースは、と
を描画するサンプルです。
コピー&ペーストして動作確認をおこなってください。
<!DOCTYPE html>
<html>
<head>
<meta charset="UTF-8">
<title>flotr2 の動作確認</title>
<script src="flotr2.min.js"></script>
<style>
body {width:650px}
div#graph {
float:left;
margin: 10px 0px 0px 0px;
width : 400px;
height: 300px;
}
div#graph canvas {
overflow : visible;
}
</style>
<script>
var d1 = [], var d2 = [];
function drow(){
var omega = Math.PI/2;
for(var i=-2; i<=2; i+=0.01){
d1.push([i, Math.sin(omega*i)]);
d2.push([i, Math.cos(omega*i)]);
}
basic_legend(document.getElementById("graph")); //図の描画
}
function basic_legend(container) {
var data, graph, i;
data = [
{ data : d1, label :'sin' }, //グラフ1のラベル
{ data : d2, label :'cos' } //グラフ2のラベル
];
// ラベルのフォーマットを決定する関数
function labelFn (label) {
return label;
}
// グラフを描画する
graph = Flotr.draw(container, data, {
legend : { // 凡例の設定
position : 'nw', // 凡例の位置(nw:north-west の略)
labelFormatter : labelFn, // ラベルのフォーマット関数を指定
backgroundColor : '#D2E8FF' // 凡例の背景色
},
yaxis : { // y軸の範囲を指定
max : 1.1,
min : -1.1
},
HtmlText : false //ラベルをHTMLテキストにするか否か
});
}
</script>
</head>
<body onload="drow();">
<div id="graph"></div>
</body>
</html>
実行結果
flotr2 の基本的な使い方
flotr2 も Three.js の場合と同様、HTML5 の canvas 要素を動的に生成し、その中に描画します。 本節では、Three.js を利用したときと同様に、キャンバスの額縁に相当する div 要素を予め用意し、そのサイズを CSS で指定します。 flotr2 にてx-y平面のグラフを描画するには、グラフ化したい[xの値, yの値]の組を配列化したデータを用意します。 データの配列化は
var d1 = []; d1.push([x1の値, y1の値]); d1.push([x2の値, y2の値]); d1.push([x3の値, y3の値]); ・・・
とします。複数のグラフを同時に描画するには、配列化されたデータをそれぞれ用意します。 あとはプログラム中のコメントを見れば、大体の意味は理解することができます。また、 各種プロパティはflotr2の公式ドキュメントをご覧下さい。
flotr2 の基本的な使い方2(アニメーション)
物理シミュレータでは、物理量の時間発展のリアルタイムで描画を行いたいわけですが、 Three.jsと同様、「 window.requestAnimationFrame(loop)」を利用して、 「loop()」関数内で配列化されたグラフデータを用意することで、 グラフのアニメーションを実行することができます。
var t = 0; //時刻
var dt = 0.05; //時間刻み
var d1 = []; var d2 = [];
function loop() {
t += dt;
omega = Math.PI/2;
d1.push([t, Math.sin(omega*t)]);
d2.push([t, Math.cos(omega*t)]);
if(d1.length > 100) {
d1.shift();
d2.shift();
}
basic_legend(document.getElementById("graph")); //図の描画
window.requestAnimationFrame(loop);
}
「shift();」は、配列の先頭のインデックスを削除するメソッドです。データ数が一定量に達したら、配列の一番古い座標データを削除します。
実行結果
物理量のリアルタイムグラフ描画
ここまで来れば、単振子シミュレータに物理量のリアルタイムグラフ描画を追加することは簡単です。 ここでは、時刻t に対するおもりの z座標と張力のグラフを追加します。 「loop()」関数に[時刻,z座標]と[時刻,張力]の座標データを配列化するだけです。
d1.push([t, ball.tension()]);
d2.push([t, ball.z]);
if(d1.length > 100) {
d1.shift();
d2.shift();
}
実行結果
以下の図は実行画面のキャプチャです。実際の実行画面は「サンプル4-4」をご覧下さい。
以下はデモページのキャプチャ画象です → デモページへ
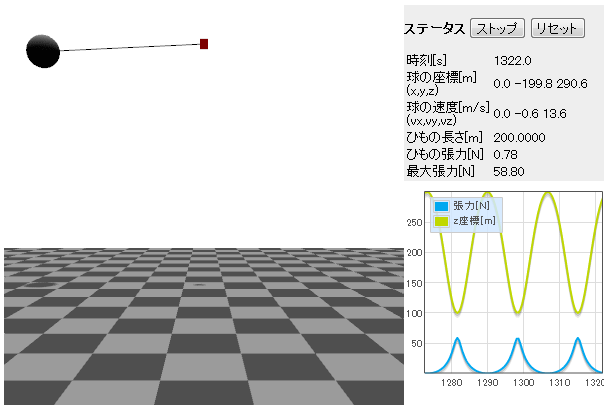
パート2の目的である単振子シミュレータはここで完成となります。 あとは、Three.js を勉強中に見つけた「」
おまけ
GUIによるパラメータの変更(dat.gui の利用)
「dat.gui」とはGoogle の Data Arts Team が開発した Javascript をグラフィカルにコントロールするためのライブラリです。 デモページに移動し、右上のコントローラーにあるバーをスライドしてみてください。 おもりのスケールを「0.1」から「10」まで変更できます。
以下の図は実行画面のキャプチャです。実際の実行画面は「サンプル4-5」をご覧下さい。
以下はデモページのキャプチャ画象です → デモページへ
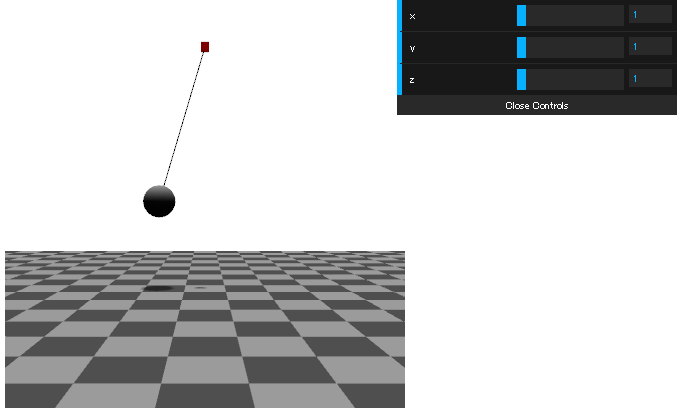
設置も簡単で、 head 要素内で、「DAT.GUI.min.js」を読み込み、「loop()」関数内に
var gui = new DAT.GUI(); // DAT.GUI クラスのオブジェクトを宣言
gui.add(ball.object.scale, 'x', 0.1, 10, 0.1);
gui.add(ball.object.scale, 'y', 0.1, 10, 0.1);
gui.add(ball.object.scale, 'z', 0.1, 10, 0.1);
と記述するだけです。 利用するにはhttp://workshop.chromeexperiments.com/examples/gui/#1--Basic-Usageの右下にある「DAT.GUI.min.js」をダウンロードしてください。
Ballクラスのオブジェクトの配列化
初期値の違いによる運動の違いを比較したい場合、異なる初期値の運動を同時に描画することで理解しやすくなります。 そのような場合、Ballクラスのオブジェクトを配列化することで簡単に実現することができます。 本節では、おもりにz方向に異なる初速度を与えた場合の運動を比較します。
var Ball = function(m,x,y,z,vx,vy,vz){
this.m = m;
this.x = x; this.y = y; this.z = z;
this.vx = vx; this.vy = vy; this.vz = vz;
};
var ball = new Array();
for(var i=0; i<5; i++){
ball[i] = new Ball(1, 0, L, 300, 0, 0, i*5);
}
以下の図は実行画面のキャプチャです。実際の実行画面は「サンプル4-6」をご覧下さい。
以下はデモページのキャプチャ画象です → デモページへ
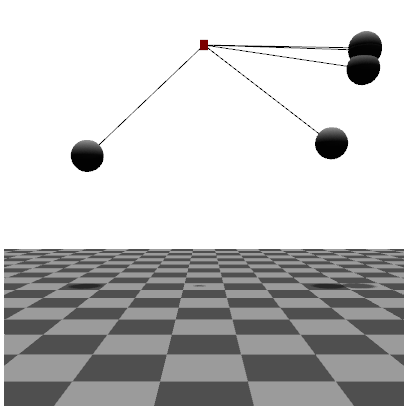
パート3では、いよいよ2重振り子シミュレータを完成させます。












































