HTML5による有限要素法に基づいた2次元弾性体変形シミュレーション 第1回
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解
有限要素法(Finite Element Method, 以下, FEM)は
物理現象の高精度な計算に向いている数値解析手法です。
研究やものづくりでよく使われるほか、
コンピュータグラフィクスにも応用され
エンターテイメントの分野でも活躍しています。
物体の変形計算方法としては、
質点をばねダンパで結合した機械要素ネットワークによって
物体の変形を表現する、Spring Network Modelがよく用いられています。
Spring Network Modelと比較して、FEMは理論が難しく計算量も大きくなります。
しかし、物理的に正しい(連続体力学に基づいた)計算ができるため、
よりリアルな変形表現が可能となります。
近年のPCはFEMをリアルタイム計算するのに十分な計算性能を有しています。
今後ますます身近になると予想されるこの技術の実装方法を、
HTML5を活用しブラウザ上で体験していただくことがこの記事の目的です。
内容
記事作成予定を変更しました(2013/11/02)。4~5回で完結するように記事を作成します。この記事では、FEMによる2次元物体変形計算の実装方法をメインテーマとし、 以下の内容を説明します。
・FEMの実装方法(データ構造、計算方法)
・HTML5 Canvas要素による可視化
・線形代数ライブラリNumeric.jsによる数値計算
この記事は数回に分けて作成する予定です。
まず、初めにFEMのモデル表現に欠かせないメッシュのデータ構造を説明し、 長方形を規則的な三角形の集合としてメッシュ分割する例を実装します。 さらにそのメッシュをCanvas要素に描画する方法を述べます。

ステップ1 四角形物体のメッシュ分割とCanvas要素による可視化
次に変形計算に必要となる行列演算と連立方程式の解法について述べます。 これらの煩雑な演算は線形代数ライブラリNumeric.jsを用いて実現します。 変形計算の具体的な手続きはその後に取り扱います。
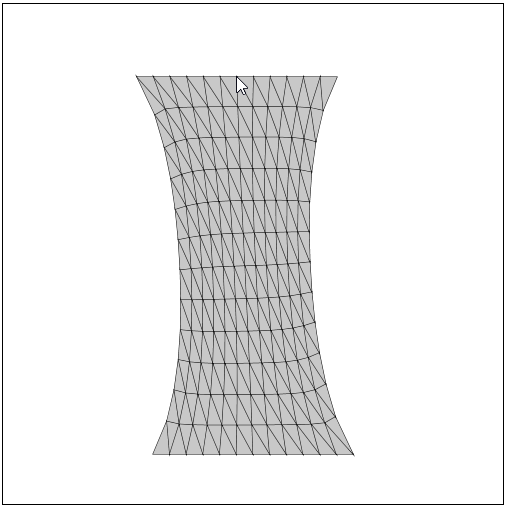
ステップ2 変形計算の手続きとNumeric.jsによる行列演算の実装
最後に応力状態を可視化する方法について述べます。 応力場をスカラー場(最大主応力やミーゼス応力)に変換して色によって表現する方法と 応力テンソル場を矢印で表現する方法を示します。
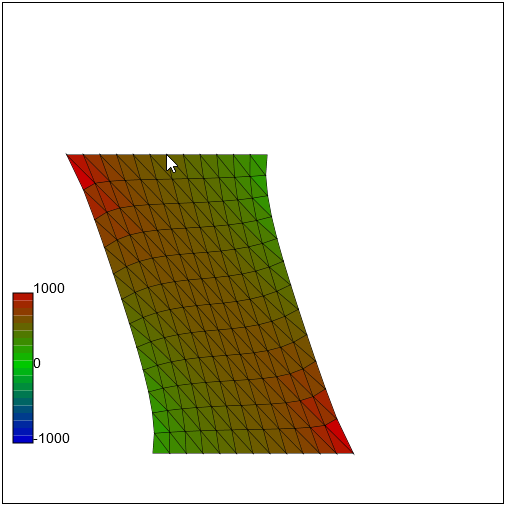

ステップ3 応力状態の可視化方法
なお、ここで述べるのは二次元の静的なつりあいを満たす変形形状を計算する方法です。
2次元三角形定ひずみ要素を例に静的FEMの実装方法を述べます。
より高精度なFEMやダイナミックな柔軟物体アニメーション手法は今後の記事をご期待いただきたいと思います。
以下、第1回の本文です。
FEMのデータ構造
FEMで物体の変形を計算するためには、物体形状を
三角形などの単純形状で分割します。
分割した一つ一つの三角形を要素、
要素の頂点を節点と呼びます。
これらの集合をメッシュと呼び、それを表現する最も簡単なデータ構造は以下のようになります。
・節点の位置
・要素を構成する節点番号リスト
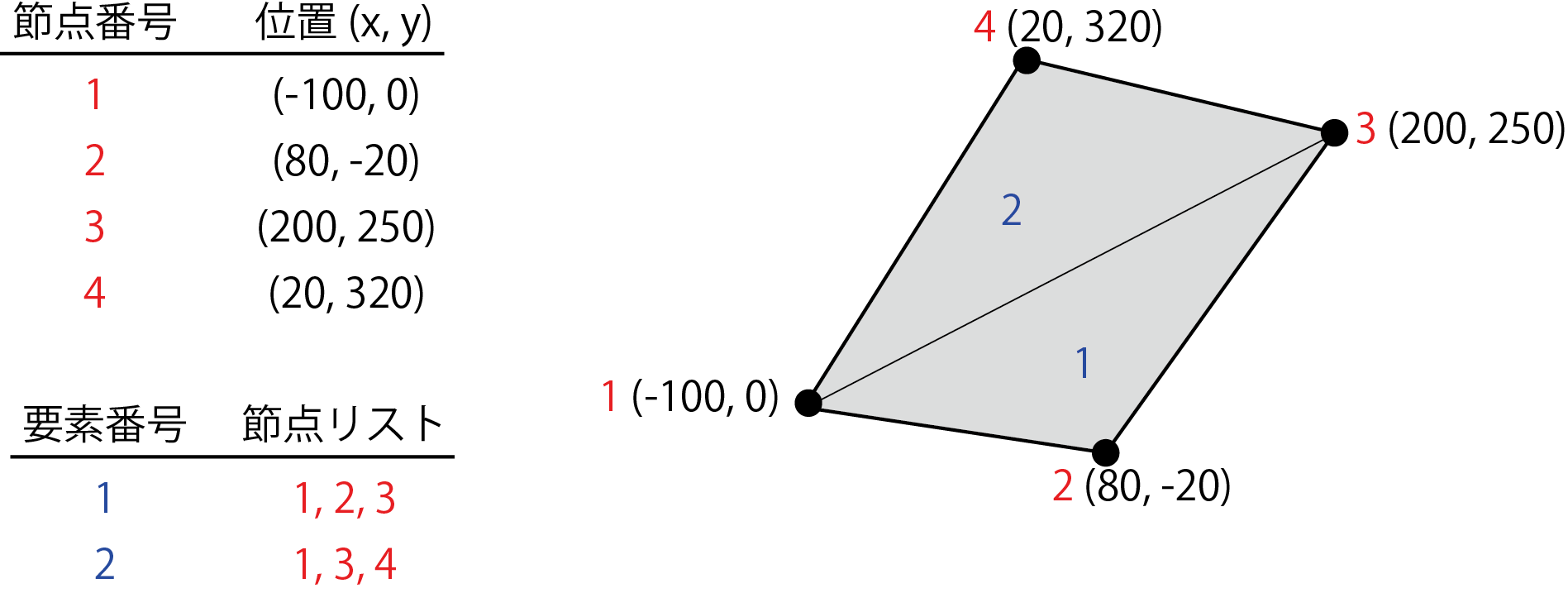
メッシュとデータ構造の例
FEMではメッシュの初期形状と現在形状を持つ必要があります。 これらを満たす最低限のクラスを以下のように作ることにします。
function FEM(){
this.pos = []; // 節点の初期位置
this.initpos = []; // 節点の現在位置
this.tri = []; // 三角形要素の節点番号リスト
}
上に示した図の例の場合、次のように書けます。 プログラムではインデックスを0からに振りなおしています。
function FEM(){
this.pos = [[-100,0], [80,-20], [200,250], [20,320]];
this.initpos = [[-100,0], [80,-20], [200,250], [20,320]];
this.tri = [[0,1,2], [0,2,3]];
}
メッシュのデータ格納法は以上です。 次にこのデータをCanvas要素で可視化します。
Canvas要素によるメッシュ描画
次のHTML文書はCanvas要素に円を描画するjavascriptコードを含んでいます。 円を描画する位置は(100, 200)としています。 HTML文書として保存し、ブラウザで開くと下に示す図が描画されます。
<!doctype html>
<html>
<head>
<meta charset="utf-8">
<title>FEM</title>
<!-- スタイルシート -->
<style type="text/css">
#model_viewer{
width: 500px;
height: 500px;
border: 1px solid #000000;
background-color: #FFFFFF;
}
</style>
<!-- jquery -->
<script type="text/javascript" src="http://ajax.googleapis.com/ajax/libs/jquery/1/jquery.min.js"></script>
<!-- 自分のjavascriptコード -->
<script type="text/javascript">
// HTMLを読み終わった後に実行する関数
$(document).ready(function() {
// 2dコンテキスト取得
var canvas = $("#model_viewer");
var context = canvas.get(0).getContext("2d");
// 要素の大きさと描画領域の大きさを合わせる
canvas.get(0).width = canvas.get(0).clientWidth;
canvas.get(0).height = canvas.get(0).clientHeight;
// 円の描画
var p = [100, 200];
context.beginPath();
// 位置p, 半径20pxの円を描画する
context.arc( p[0], p[1], 20, 0, 2*Math.PI, true);
context.stroke();
context.fill();
});
</script>
</head>
<body>
<canvas id="model_viewer">
</body>
</html>

上のコードの実行結果
この結果からもわかるようにcanvas要素のデフォルト座標系は
要素左上を原点とし右方向にX軸, 下方向にY軸が伸びています。
一方物理では上方向にY軸が伸びるように座標をとることが普通なので座標変換を行います。
そこでCanvas要素のsetTransformメソッドを使って座標変換を行います。
下に示すような座標変換を実行するためには次のようにメソッドを実行します。
context.setTransform(1, 0, 0, -1, xzero, yzero);
この記述以降はsetTransformメソッドを再び呼び出すまで この座標変換が適用されます。
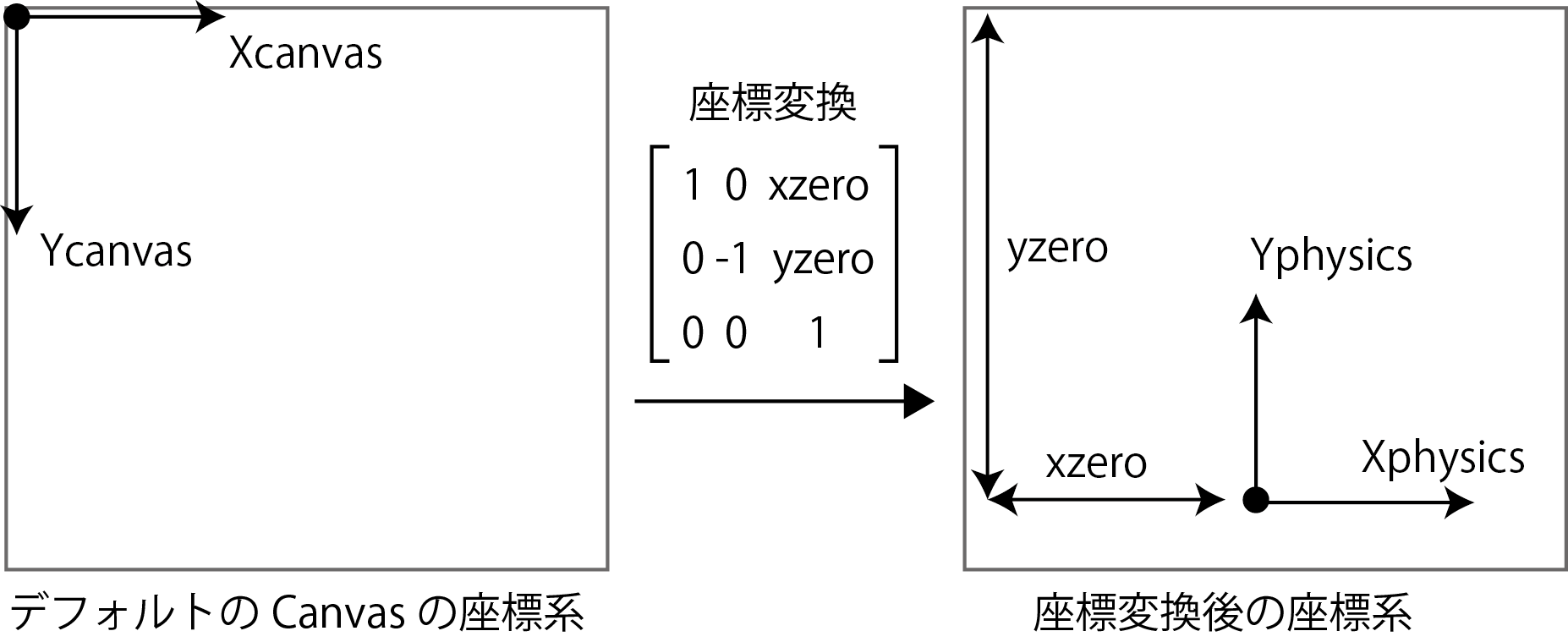
座標変換
座標変換を元に戻す必要があるときは以下のメソッドを記述してください。
context.setTransform(1, 0, 0, 1, 0, 0);
setTransformメソッドによる座標変換を確認するために上で示したHTML文書のjavascriptコード部分を以下のように修正して実行してみます。 なお、今度は原点(0,0)と(100, 200)の位置に円を描画しています。
$(document).ready(function() {
// 2dコンテキスト取得
var canvas = $("#model_viewer");
var context = canvas.get(0).getContext("2d");
canvas.get(0).width = canvas.get(0).clientWidth;
canvas.get(0).height = canvas.get(0).clientHeight;
var canvasWidth = canvas.get(0).width;
var canvasHeight = canvas.get(0).height;
// 座標変換
var xzero = canvasWidth * 0.5; // キャンバス要素の幅の半分
var yzero = canvasHeight * 0.9; // キャンバス要素の高さの90%の部分
context.setTransform(1,0,0,-1,xzero,yzero); // 座標変換
// 円の描画
var p;
p = [0, 0];
context.beginPath();
context.arc( p[0], p[1], 20, 0, 2*Math.PI, true);
context.stroke();
context.fill();
// 円の描画
p = [100, 200];
context.beginPath();
context.arc( p[0], p[1], 20, 0, 2*Math.PI, true);
context.stroke();
context.fill();
});

座標変換後の描画結果
この座標変換のもとでFEMクラスのメッシュを描画してみます。 ここでは今後頻繁に使うことになる円、三角形、線分の描画関数を用意しました。 実行結果を下の図に示します。FEMのメッシュが描画できていることが確認できます。
$(document).ready(function() {
// FEMクラスの定義
function FEM(){
this.pos = [[-100,0], [80,-20], [200,250], [20,320]];
this.initpos = [[-100,0], [80,-20], [200,250], [20,320]];
this.tri = [[0,1,2], [0,2,3]];
}
// FEMクラスのインスタンス化
var fem = new FEM();
// 2dコンテキスト取得
var canvas = $("#model_viewer");
var context = canvas.get(0).getContext("2d");
canvas.get(0).width = canvas.get(0).clientWidth;
canvas.get(0).height = canvas.get(0).clientHeight;
var canvasWidth = canvas.get(0).width;
var canvasHeight = canvas.get(0).height;
// 座標変換
var xzero = canvasWidth * 0.5; // キャンバス要素の幅の半分
var yzero = canvasHeight * 0.9; // キャンバス要素の高さの90%の部分
context.setTransform(1,0,0,-1,xzero,yzero);
// メッシュの描画
for(var i=0; i<fem.tri.length; i++){
drawTri(fem.pos[fem.tri[i][0]],fem.pos[fem.tri[i][1]],fem.pos[fem.tri[i][2]]);
}
// 線の描画関数
function drawLine(p1, p2){
context.beginPath();
context.moveTo( p1[0], p1[1]);
context.lineTo( p2[0], p2[1]);
context.stroke();
}
// 円の描画関数
function drawCircle(p, radius){
context.beginPath();
context.arc( p[0], p[1], radius, 0, 2*Math.PI, true);
context.stroke();
context.fill();
}
// 三角形の描画関数
function drawTri(p1, p2, p3){
context.beginPath();
context.moveTo( p1[0], p1[1]);
context.lineTo( p2[0], p2[1]);
context.lineTo( p3[0], p3[1]);
context.closePath();
context.stroke();
}
});
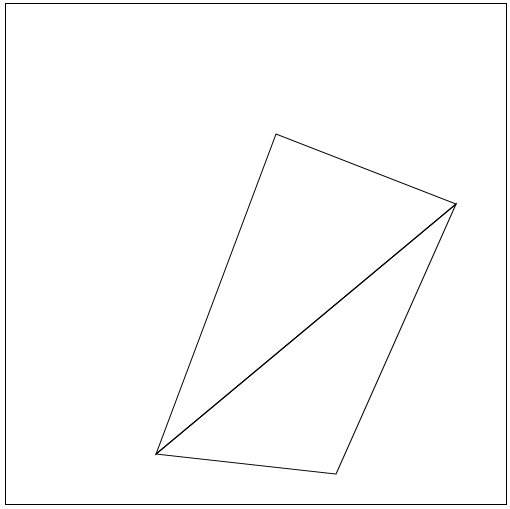
FEMクラスのメッシュをCanvas要素に描画
四角形の三角形分割
長方形の規則的な三角形分割の具体的な例を示します。 メッシュ生成の手順は下の図に示すように、境界を設定、点を配置、三角形分割という流れになります。
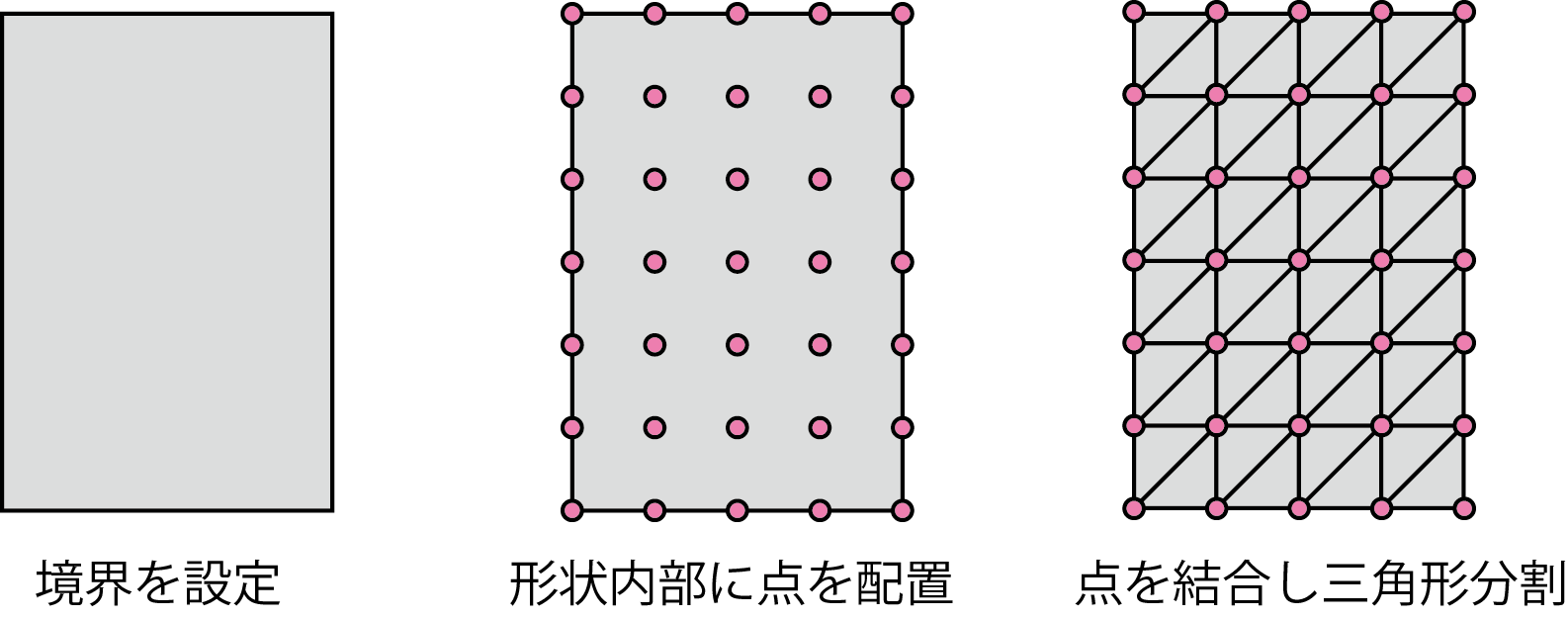
長方形の三角形分割
境界の設定では下の図のように、長方形の幅、高さ、左下の座標を定義します。
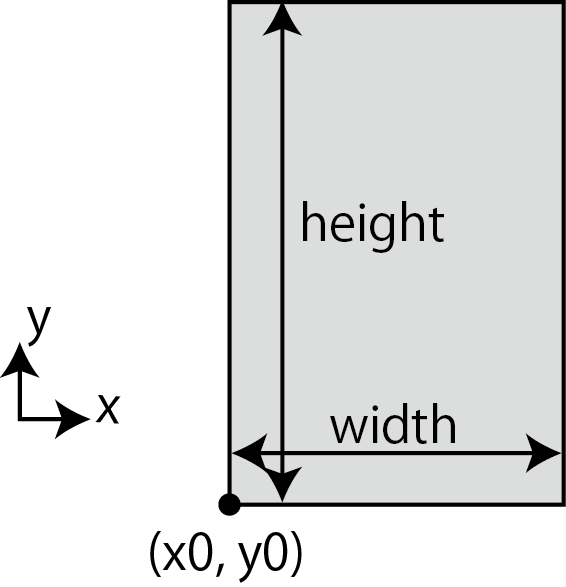
長方形の境界の設定
点の配置のために辺の分割数を設定します。 x方向の分割数をdivx, y方向の分割数をdivyと呼ぶことにします。 点の数は (divx + 1)*(divy + 1) 個となります。 これらの点をそのままFEMの節点とするので FEMクラスのPosプロパティを2次元配列(行数:節点数,列数:次元数(=2))として 格納していきます。 節点番号は左下から行ごとに振っていきます。 点の座標は長方形の辺の長さと分割数から計算します。 図にdivx = 4, divy = 6 の例を示します。
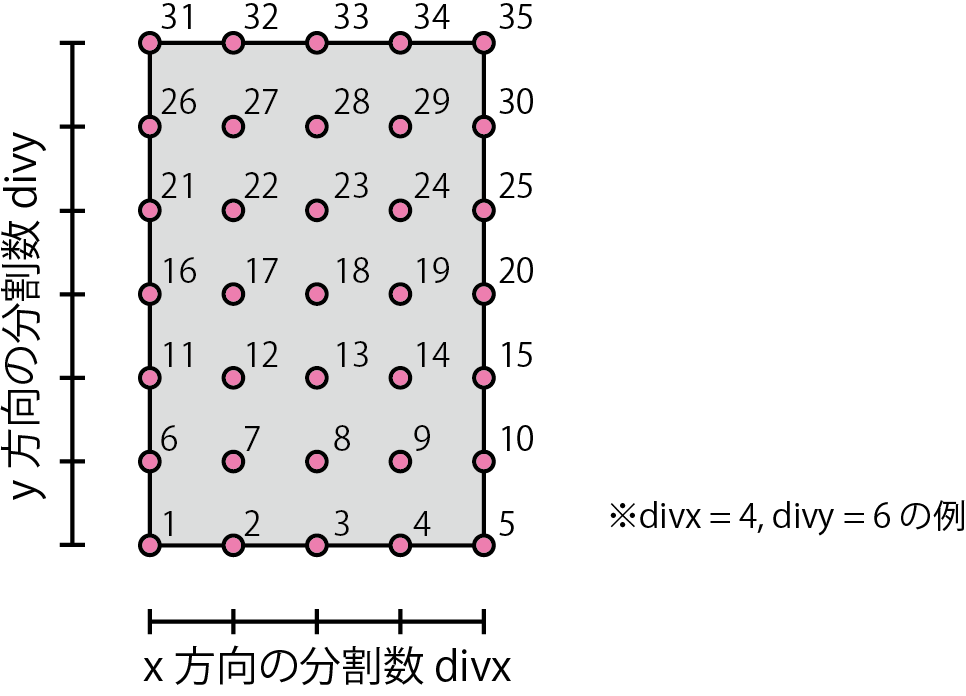
長方形内部への点の配置
次に配置した点を結合して三角形分割します。 三角形の数は 2*divx*divy 個となります。 この分割でえられた三角形番号と節点番号の対応リストを、 FEMクラスのTriプロパティを2次元配列(行数:三角形数,列数:頂点数(=3))として格納していきます。 三角形の番号は左下から順に番号を振ります。
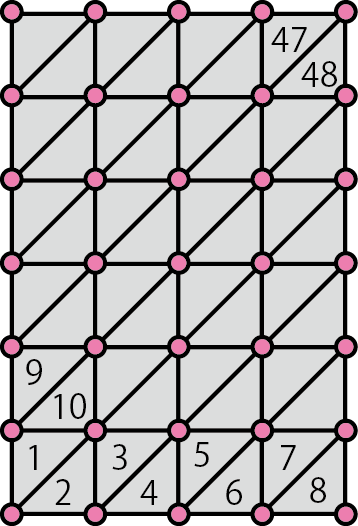
配置した点を結合して三角形分割
以上の分割方法をFEMクラスに実装した例を示します。
新たにrectangleMeshメソッドを追加しました。
メッシュ生成の開始点座標は(-width*0.5, 0)としました。
これによって生成される長方形モデルは底面が y = 0 でY軸対称となります。
(この実装ではメッシュは対称になりません)
なお、これまでのイラストと異なりプログラム中では節点と三角形のインデックスが0から振られることに注意してください。
$(document).ready(function () {
// FEMクラス
function FEM() {
this.pos = []; // 節点現在位置の座標リスト
this.initpos = []; // 節点初期位置の座標リスト
this.tri = []; // 三角形メッシュの節点番号リスト
}
// 三角形メッシュ生成メソッド
FEM.prototype.generateTriangleMesh = function (width, height, divx, divy) {
for(var i = 0; i < divy + 1; i++) {
for(var j = 0; j < divx + 1; j++) {
this.pos.push([width / divx * j - width * 0.5, height / divy * i]);
this.initpos.push([width / divx * j - width * 0.5, height / divy * i]);
}
}
for(var i = 0; i < divy; i++) {
for(var j = 0; j < divx; j++) {
this.tri.push([j + 1 + (divx + 1) * i, j + 1 + (divx + 1) * (i + 1), j + (divx + 1) * (i + 1)]);
this.tri.push([j + (divx + 1) * i, j + 1 + (divx + 1) * i, j + (divx + 1) * (i + 1)]);
}
}
}
// FEMクラスのインスタンス化
var fem = new FEM();
// 三角形メッシュの生成
fem.generateTriangleMesh(200, 200, 5, 5);
// 2dコンテキスト取得
var canvas = $("#model_viewer");
var context = canvas.get(0).getContext("2d");
canvas.get(0).width = canvas.get(0).clientWidth;
canvas.get(0).height = canvas.get(0).clientHeight;
var canvasWidth = canvas.get(0).width;
var canvasHeight = canvas.get(0).height;
// 座標変換
var xzero = canvasWidth * 0.5; // キャンバス要素の幅の半分
var yzero = canvasHeight * 0.9; // キャンバス要素の高さの90%の部分
context.setTransform(1, 0, 0, -1, xzero, yzero);
// メッシュの描画
for(var i = 0; i < fem.tri.length; i++) {
drawTri(fem.pos[fem.tri[i][0]], fem.pos[fem.tri[i][1]], fem.pos[fem.tri[i][2]]);
}
// 線の描画関数
function drawLine(p1, p2) {
context.beginPath();
context.moveTo(p1[0], p1[1]);
context.lineTo(p2[0], p2[1]);
context.stroke();
}
// 円の描画関数
function drawCircle(p, radius) {
context.beginPath();
context.arc(p[0], p[1], radius, 0, 2 * Math.PI, true);
context.stroke();
context.fill();
}
// 三角形の描画関数
function drawTri(p1, p2, p3) {
context.beginPath();
context.moveTo(p1[0], p1[1]);
context.lineTo(p2[0], p2[1]);
context.lineTo(p3[0], p3[1]);
context.closePath();
context.stroke();
}
});
generateTriangleMeshに与える引数を変えて実行してみると下の図のように任意な長方形と 指定した分割数のメッシュを生成することができます。
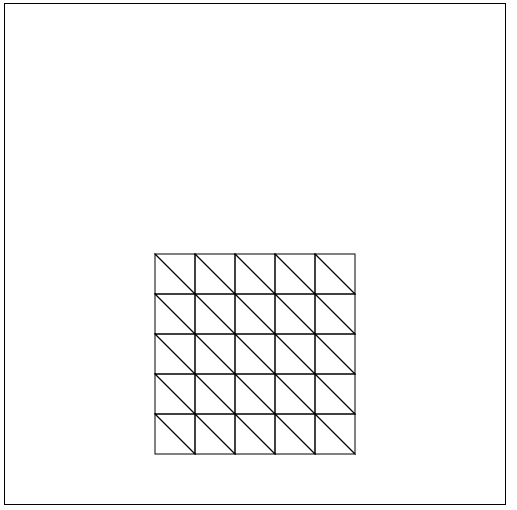

FEMクラスgenerateTriangleMeshメソッドの実行例
第1回は以上です。
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解
























