HTML5による有限要素法に基づいた2次元弾性体変形シミュレーション 第3回
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解
第3回では有限要素法(FEM)における変形表現と境界条件の設定について解説します。 変形の表現はメッシュ構造と変位ベクトルの集合によって実現されます。 FEMでは変位ベクトルと外力ベクトルの関係を結びつける方程式を数値的に解きます。 本記事では実例とともに変形表現のデータ構造をjavascriptにより実装しながら解説します。また方程式を解く前段階として不可欠なステップである境界条件の設定についてデータ構造と実装を交えて解説します。
変形の表現
物体の形状はメッシュのデータ構造を用いて節点と三角形要素によって表すことができました(第1回 メッシュのデータ構造とCanvas要素による描画)。
物体の初期形状のメッシュデータを持っているとき,各節点の変位ベクトルを定義することでメッシュの変形を表現することができます。
具体例として四角形物体の圧縮変形の例を下の図に示します。
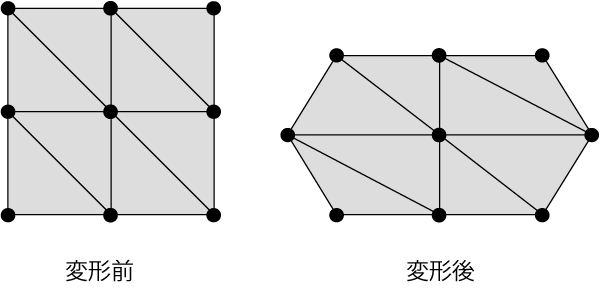
変形前後の形状を比較するためメッシュを重ねてみます。 変形前の形状はメッシュデータとして持っているので,各節点に変位ベクトルを定義すれば変形後の形状を得ることができることが確認できます。
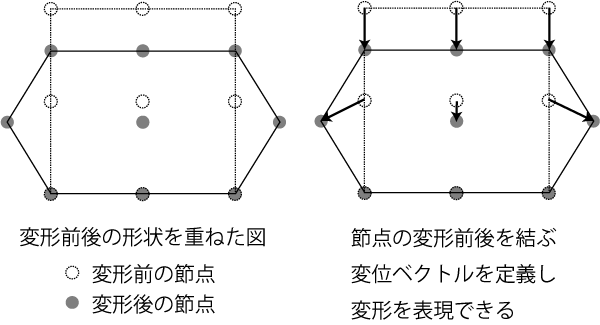
メッシュを細かくしていけば形状が滑らかになっていきます。
極限まで細かくすれば、変位ベクトルは物体内部で連続的に分布する変数となり、変位ベクトル場を成します。
連続的な変形表現をすることで物体の変形が偏微分方程式により記述でき、数式で解析的に扱うことができます。
本記事では離散的なデータ構造から連続的な場の説明に至りましたが、教科書では逆のアプローチをするのが普通で、
各種物理場の定義から偏微分方程式の導出、それから離散化と進んでいきます。
さてFEMでは変位ベクトルを縦につなげて大きな列ベクトルを作成し、これを全体変位ベクトルと呼びます。
今回の例では下の図のようになります。
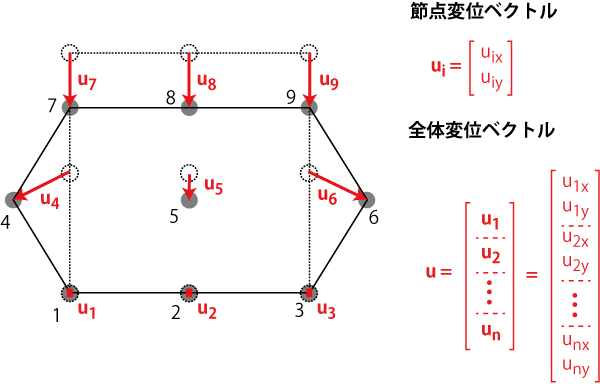
二次元問題では全体変位ベクトルは節点数nのとき2n次元の列ベクトルとなります。
それではこれらのデータ構造により任意の変形形状が表現できることを、javascriptで実装して確認してみましょう。
今回からはHTMLファイルとjavascriptファイルを分離します。
HTMLファイルとしてindex.html,javascriptファイルとしてfem.js,main.jsを作成します。
fem.jsはFEMクラスの定義,main.jsは主要な処理と描画,イベント処理を記述することにします。
fem.jsとmainjsはindex.htmlと同じディレクトリに配置してください。
index.html
18行目でnumeric.js,20行目でfem.js,21行目でmain.jsを読み込みます。 fem.jsでnumeric.jsを,main.jsでfem.jsを参照したいので,この順序は変更できません。
<!doctype html>
<html>
<head>
<meta charset="utf-8">
<title>FEM</title>
<!-- スタイルシート -->
<style type="text/css">
#model_viewer {
width: 500px;
height: 500px;
border: 1px solid #000000;
background-color: #FFFFFF;
}
</style>
<!-- jquery -->
<script type="text/javascript" src="http://ajax.googleapis.com/ajax/libs/jquery/1/jquery.min.js"></script>
<!-- numeric javascript -->
<script type="text/javascript" src="numeric-1.2.6.min.js"></script>
<!-- 自分のjavascriptコード -->
<script type="text/javascript" src="fem.js"></script>
<script type="text/javascript" src="main.js"></script>
</head>
<body>
<canvas id="model_viewer"></canvas>
</body>
</html>
fem.js
新しいメンバとして全体変位ベクトルを追加し,メッシュ生成の最後にnumeric.jsのメソッドを使って零ベクトルに初期化しています。
// JavaScript source code
function FEM() {
this.pos = []; // 節点の初期位置
this.initpos = []; // 節点の現在位置
this.tri = []; // 三角形要素の節点番号リスト
this.u = []; // 全体変位ベクトル
}
// 三角形メッシュ生成メソッド
FEM.prototype.generateTriangleMesh = function (width, height, divx, divy) {
// 節点の現在位置・初期位置の作成
for(var i=0; i<divy+1; i++) {
for(var j=0; j<divx+1; j++) {
this.pos.push([width/divx*j-width*0.5, height/divy*i]);
this.initpos.push([width/divx*j-width*0.5, height/divy*i]);
}
}
// 三角形メッシュの作成
for(var i=0; i<divy; i++) {
for(var j=0; j<divx; j++) {
this.tri.push([j+1+(divx+1)*i, j+1+(divx+1)*(i+1), j+(divx+1)*(i+1)]);
this.tri.push([j+(divx+1)*i, j+1+(divx+1)*i, j+(divx+1)*(i+1)]);
}
}
// 全体変位ベクトルの初期化
this.u=numeric.rep([2*this.pos.length], 0);
}
main.js
22行目から全体変位ベクトルに値を設定しています。数値で見るとわかりにくいですが,実行結果を見ればこのベクトルがあらわす変形形状が確認できます。
全体変位ベクトルに設定する値を変え,変形形状に反映されることをぜひ確認してみてください。
32行目から全体変位ベクトルを節点初期位置に加算することで節点現在位置を更新しています。
// JavaScript source code
// HTMLを読み終わった後に実行する関数
$(document).ready(function () {
// FEMクラスのインスタンス化
var fem = new FEM();
// メッシュ生成
fem.generateTriangleMesh(200, 200, 2, 2);
// 変位ベクトルの設定
fem.u[2*3] = -40;
fem.u[2*3+1] = -20;
fem.u[2*4+1] = -20;
fem.u[2*5] = 40;
fem.u[2*5+1] = -20;
fem.u[2*6+1] = -40;
fem.u[2*7+1] = -40;
fem.u[2*8+1] = -40;
// 変位ベクトルによる現在形状の更新
for(var i=0; i<fem.pos.length; i++) {
for(var j=0; j<2; j++){
fem.pos[i][j] = fem.initpos[i][j] + fem.u[2*i+j];
}
}
// 2dコンテキスト取得
var canvas = $("#model_viewer");
var context = canvas.get(0).getContext("2d");
canvas.get(0).width = canvas.get(0).clientWidth;
canvas.get(0).height = canvas.get(0).clientHeight;
var canvasWidth = canvas.get(0).width;
var canvasHeight = canvas.get(0).height;
// 座標変換
var xzero = canvasWidth*0.5; // キャンバス要素の幅の半分
var yzero = canvasHeight*0.9; // キャンバス要素の高さの90%の部分
context.setTransform(1, 0, 0, -1, xzero, yzero);
// 初期形状の描画
context.strokeStyle = 'black';
for(var i=0; i<fem.tri.length; i++) {
drawtri(fem.initpos[fem.tri[i][0]], fem.initpos[fem.tri[i][1]], fem.initpos[fem.tri[i][2]]);
}
// 現在形状の描画
context.strokeStyle = 'red';
for(var i=0; i<fem.tri.length; i++) {
drawtri(fem.pos[fem.tri[i][0]], fem.pos[fem.tri[i][1]], fem.pos[fem.tri[i][2]]);
}
// 線の描画関数
function drawLine(p1, p2) {
context.beginPath();
context.moveTo(p1[0], p1[1]);
context.lineTo(p2[0], p2[1]);
context.stroke();
}
// 円の描画関数
function drawCircle(p, radius) {
context.beginPath();
context.arc(p[0], p[1], radius, 0, 2*Math.PI, true);
context.stroke();
context.fill();
}
// 三角形の描画関数
function drawtri(p1, p2, p3) {
context.beginPath();
context.moveTo(p1[0], p1[1]);
context.lineTo(p2[0], p2[1]);
context.lineTo(p3[0], p3[1]);
context.closePath();
context.stroke();
}
});
このファイルの実行結果は下の図のようになります。変形例で扱った圧縮形状が得られました。
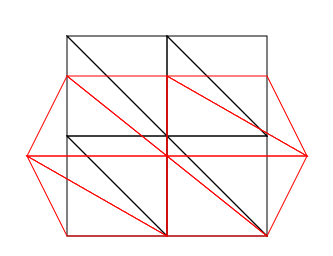
この実装ではすべての節点の変位を指定しましたが,FEMでは境界条件を設定すれば自動的に変位ベクトルが得られます。
剛性方程式
FEMでは変位ベクトルと対応した外力ベクトルを定義します。全体外力ベクトルは全体変位ベクトルと同様に2n次元の列ベクトルです。 弾性力学のつりあいの式から変位と外力の関係が得られます。
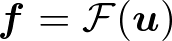
本記事で対象とする微小変形理論に基づく線形弾性体では、つりあい状態下の変位と外力の関係は次のようになります。 この方程式は剛性方程式と呼ばれています。
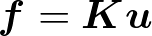
ここでKは2n×2nの行列であり剛性マトリクスと呼ばれる,
メッシュの形状と材料特性から決定される定数です。
したがって全ての変位ベクトルの値がわかっていれば,外力ベクトルは行列をベクトルに掛け合わせることで得られます。
また,この方程式は第2回で言及した連立一次方程式そのものです。
外力ベクトルの値がわかっていれば,変位ベクトルは連立一次方程式を解けば得られます。
しかし,どんな場合でも連立一次方程式が解けるとは限りません。
実際には剛性方程式を解くために適切な境界条件に基づいた行列・ベクトルの成分の並べ替えが必要となります。
これについては今後の記事で述べます。
それでは境界条件の設定方法について具体例を考えながら解説していきます。
境界条件
FEMでは境界条件として各節点について変位か外力かのどちらかの値を設定します。
下の図のように変位既知である節点(黒丸)と外力既知である節点(白丸)を区別し,
既知な値をFEMの境界条件として与えます。
環境に固定されている領域は変位がゼロとなるため変位既知,
強制的に変位を与える領域は当然変位既知となります。
変位が未知な領域では,その領域に作用する圧力、重力、電磁力、慣性力などの外力を計算して与えます。
FEMでは要素ごとにこれらの外力を等価な節点力に置き換えます。
このような処理は多少煩雑になります。
本記事においては変位既知でない節点はすべて外力が零の外力既知節点とすることで簡略化します。
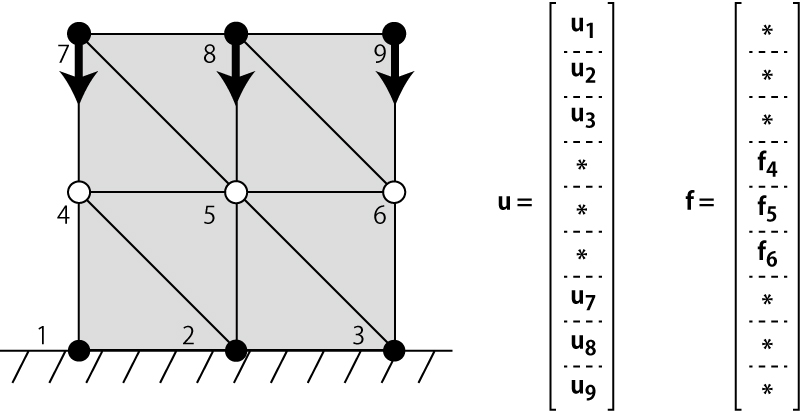
境界条件を表現するデータ構造の一例は以下のようになります。 外力既知節点リストをflist, 変位既知節点リストdlist, 既知な変位を結合した列ベクトルud, そして既知な外力を結合した列ベクトルffです。ここで添え字のf, d はそれぞれforce, displacementの頭文字です。
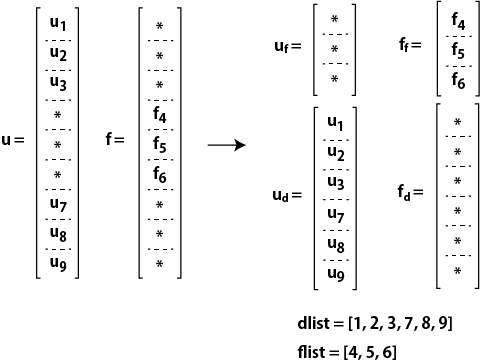
FEMクラスにこれらのメンバを追加しましょう。
ud, uf, fd, ffはメンバとして持っている必要がないので,必要な時にローカル変数を作成することにします。
function FEM(){
this.pos = []; // 現在位置
this.initpos = []; // 初期位置
this.tri = []; // 三角形メッシュの節点番号リスト
this.u = []; // 全体変位ベクトル
this.f = []; // 全体外力ベクトル
this.dlist = []; // 変位既知節点リスト
this.flist = []; // 外力既知節点リスト
}
FEMクラスに境界条件を設定する新しいメソッドを追加します。 引数は固定する節点のy座標,強制変位を与える節点のy座標,強制変位を表す2次元ベクトルです。 全体変位ベクトル・全体外力ベクトルは初めは零ベクトルで初期化しています。 すべての節点のy座標をチェックし変位既知(固定か強制変位)か外力既知かを判別します。 既知な強制変位と外力は全体変位ベクトル,全体外力ベクトルにあらかじめ格納することにします。 実際に ud, ff が必要となるのは剛性方程式の求解においてですので, solveメソッドを追加し ud, ff はこのメソッドの中で全体変位ベクトル・全体外力ベクトルから 作成するように記述しました.
// 境界条件の設定
FEM.prototype.setBoundaryCondition = function (zfix, zdisp, disp) {
this.dlist = [];
this.flist = [];
this.u = numeric.rep([2*this.pos.length], 0);
this.f = numeric.rep([2*this.pos.length], 0);
// 底面のノードに強制変位を与える
for(var i=0; i<this.pos.length; i++){
if(this.initpos[i][1] === zfix){
this.u[2*i] = 0;
this.u[2*i+1] = 0;
this.dlist.push(i);
}else if(this.initpos[i][1] === zdisp){
this.u[2*i] = disp[0];
this.u[2*i+1] = disp[1];
this.dlist.push(i);
}else{
this.f[2*i] = 0;
this.f[2*i+1] = 0;
this.flist.push(i);
}
}
}
// 剛性方程式の求解
FEM.prototype.solve = function (){
var ud = [];
var ff = [];
// udの作成
for(var i=0; i<this.dlist.length; ++i){
ud.push(this.u[2*this.dlist[i]]);
ud.push(this.u[2*this.dlist[i]+1]);
}
// ffの作成
for(var i=0; i<this.flist.length; ++i){
ff.push(this.f[2*this.flist[i]]);
ff.push(this.f[2*this.flist[i]+1]);
}
// solveメソッドは次回に続く
}
main.js で手動で変位を設定する代わりに setBoundaryCondition を呼び出した場合のFEMクラスの状態を可視化してみます。 変位既知な節点を青,外力既知な節点で描画するためにmain.jsに下記のコードを加えます。
// 変位既知節点の描画
context.strokeStyle='blue';
context.fillStyle='blue';
for(var i=0; i<fem.dlist.length; i++) {
drawCircle(fem.pos[fem.dlist[i]], 5);
}
// 外力既知節点の描画
context.strokeStyle='green';
context.fillStyle='green';
for(var i=0; i<fem.flist.length; i++) {
drawCircle(fem.pos[fem.flist[i]], 5);
}
以下のようにsetBoundaryConditionを呼び出した場合、canvasには下の図のような形状が描画されます。
// FEMクラスのインスタンス化
var fem=new FEM();
// 三角形メッシュ生成
fem.rectangleMesh(200, 200, 2, 2);
// 境界条件の設定
fem.setBoundaryCondition(0, 200, [0, -40]);
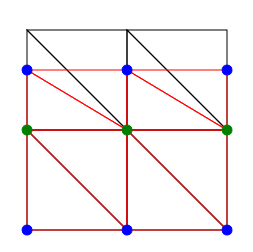
引数の強制変位のベクトルの値を変えれば境界条件に反映されます。
// 境界条件の設定 fem.setBoundaryCondition(0, 200, [10, 40]);
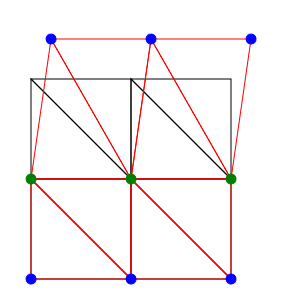
また、メッシュを細かくしても同じメソッドで境界条件を設定できます。
// FEMクラスのインスタンス化
var fem=new FEM();
// 三角形メッシュ生成
fem.rectangleMesh(200, 200, 10, 10);
// 境界条件の設定
fem.setBoundaryCondition(0, 200, [10, 40]);
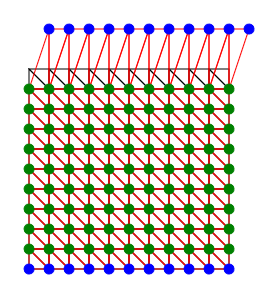
緑色で示されている節点の位置は境界条件に基づいて剛性方程式を解くことで自動的につり合いが満たされるよう計算されます。
さらに進んだ境界条件の設定
外力は要素ごとに等価な節点外力に変換すると述べました。
本記事で対象とする定ひずみ三角形要素では比較的簡単に等価節点外力を求めることができます。
圧力が印加されている面(メッシュでは辺ですが厚みがあるので面)では面積に圧力をかけて面に作用する外力を計算し,辺の端点である2つの節点に半分ずつ割り当てます。
重力を考慮する場合,三角形要素の体積に密度と重力加速度を掛けて要素に作用する外力を計算し,1/3にして3点に割り当てます。
また、今回は節点を変位既知か外力既知のどちらかに振り分けましたが、一つの節点でx方向は外力既知,y方向は変位既知という設定も可能です。
そのようにしたい場合は,変位・外力ベクトルの分割を節点変位・外力ベクトルごとではなく,その成分ごとに分割します。
第3回は以上です。
第1回 メッシュのデータ構造とCanvas要素による描画
第2回 Numeric.jsによる線形代数
第3回 変形の表現と境界条件
第4回 全体剛性マトリクスの組み立てと剛性方程式の求解























