物性物理学入門
六方最密格子

文責：遠藤理平（2016年9月15日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

六方最密格子とは結晶の原子配置の一つです。六方最密格子における原子位置は層ごとによって基本ベクトルの基準となる原点が異なります。１層目の原子の配置は以下のとおりです。

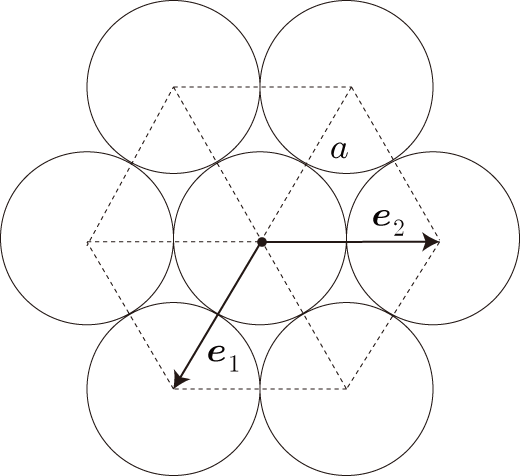
基本ベクトル $\mathbf{e}_1$ と $\mathbf{e}_1$ を上図のとおりに与えた場合、原子位置は

$\mathbf{r}_{n_1, n_2} = n_1\mathbf{e}_1 + n_2\mathbf{e}_2$

で与えられます。次の２層目は１層目の原子３個の中間に配置されます。

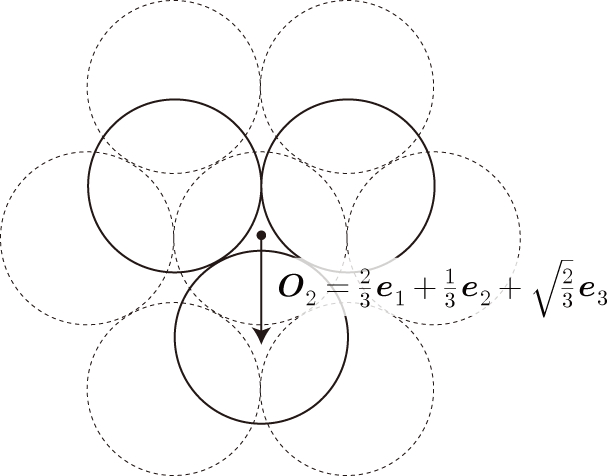
１層目の原点から２層目の原点への位置ベクトルは、面に垂直方向をz軸とすると

$\mathbf{O}_2 = \frac{2}{3}\,\mathbf{e}_1 + \frac{1}{3}\,\mathbf{e}_2 +\sqrt{\frac{2}{3}}\,a\hat{\mathbf{z}}$

で与えられます。２層目の原子配置は

$\mathbf{r}_{n_1, n_2} = \mathbf{O}_2 + n_1\mathbf{e}_1 + n_2\mathbf{e}_2$

となります。三層目の原点は１層目と同じです。そのため、 n_3 層目の原子位置は

$\mathbf{r}_{n_1, n_2, n_3} = \mathbf{O}(n_3) + n_1\mathbf{e}_1 + n_2\mathbf{e}_2 + n_3\mathbf{e}_3$

となります。ただし、

$\mathbf O(n_3)=\left\{\matrix{ 0 & (n_3 =0,2,4\cdots) \cr \frac{2}{3}\,\mathbf{e}_1 + \frac{1}{3}\,\mathbf{e}_2 & (n_3 =1,3,5\cdots) }\right.$

です。なお、 $\mathbf{e}_1$ をx軸と一致させたときの基本ベクトルは次のとおりです。

$\mathbf{e}_1 = a \hat{\mathbf{x}}$
$\mathbf{e}_2 = -\frac{1}{2}\,a \hat{\mathbf{x}} +\frac{\sqrt{3}}{2}\,a \hat{\mathbf{y}}$
$\mathbf{e}_3 = \sqrt{\frac{2}{3}} a \hat{\mathbf{z}}$

次のグラフィックスは $-4\leq n_1\leq 4$ , $-4\leq n_2\leq 4$ , $0\leq n_3\leq 7$ で指定される原子を表示しています。描画する層数を下部のインプットボックスで指定することができます。

六方最密格子の断面

六方最密格子の最近接結合・第二近接結合

物理シミュレーションについては「HTML5による物理シミュレーション」を参照ください。数式の表示は「Tex表記によるHTML文書への式の埋め込み」をご覧ください。

	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】
	「natural science 科学・技術講座」講師３人で設立した株式会社weCAN。アイディアの商品化第一弾「美姿勢メガネ」を朝日新聞さんに取材いただきました。 2021.08.23 【遠藤理平｜パブリシティ】

物性物理学入門
六方最密格子

六方最密格子の断面

六方最密格子の最近接結合・第二近接結合

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

物性物理学入門六方最密格子

六方最密格子の断面

六方最密格子の最近接結合・第二近接結合

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

物性物理学入門
六方最密格子