【量子力学再入門4】
ステップ関数型ポテンシャルへの衝突

文責：遠藤理平（2018年4月25日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。４回目のテーマは「ステップ関数型ポテンシャル障壁への衝突」です。

対象とする系：ステップ関数型ポテンシャル障壁へ衝突する量子粒子

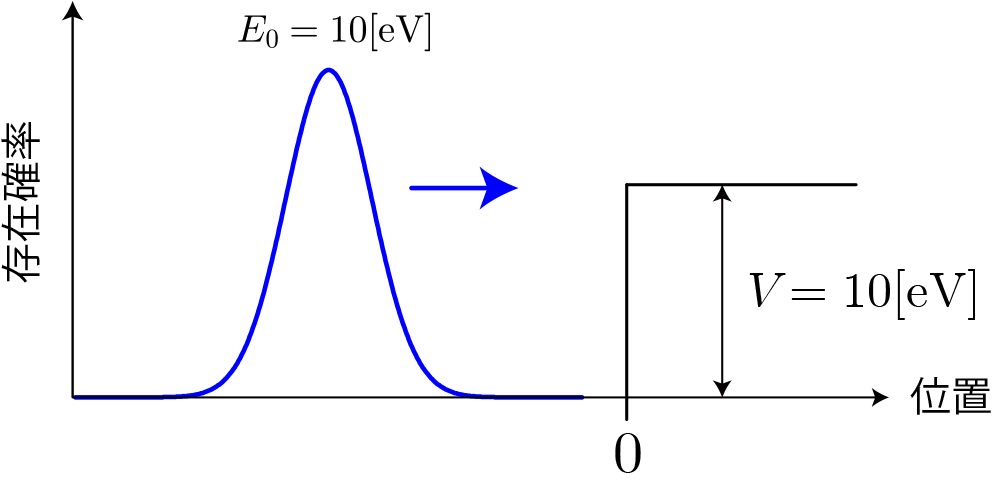
今回のステップ型ポテンシャル障壁とは、x≧0で有限の高さの段差のようにポテンシャルが存在する系です。前回の「無限に高いポテンシャル障壁」の場合にはポテンシャルが無限大のために量子粒子はすべて反射されましたが、ステップ型ポテンシャル障壁の場合にはx≧0の領域にも波束は侵入することができます。このようなポテンシャル障壁が存在する系でもそれぞれの領域で存在しうる平面波の重ね合わせで波束の運動をシミュレーションすることができます。

ステップ関数型ポテンシャルの定義

$V(x)=\left\{ \matrix{ V & (x\geq 0)\cr 0 &(x<0) } \right.$

ちなみに、量子粒子波束の中心エネルギーはE_0=10[\rm eV]（電子では光速の約0.6%）を与えているので、ポテンシャルの高さも10[\rm eV]を想定します。この場合、波束を構成している運動エネルギー成分のうち半分がポテンシャルエネルギーよりも低くなることを意味します。

ステップ関数型ポテンシャル障壁へ衝突する平面波解

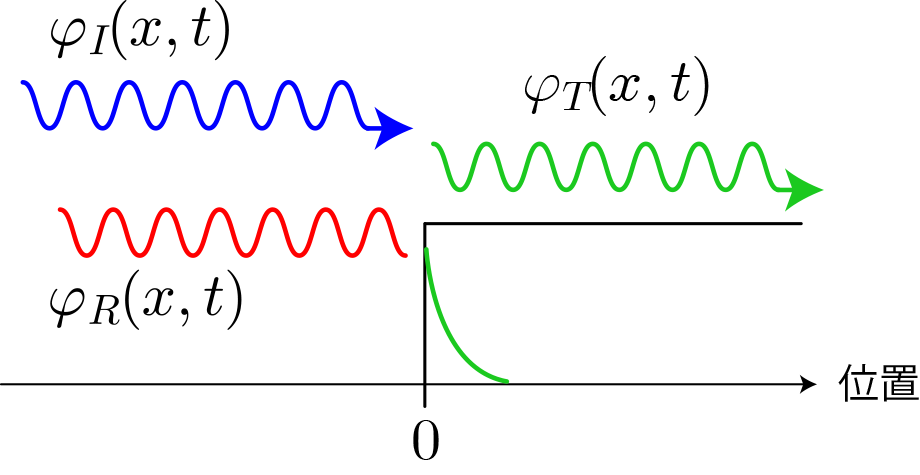
図はx>0とx≧0の領域における単一平面波の模式図です。入射波、反射波、透過波の波動関数をそれぞれ $\varphi_I(x,t)$ 、 $\varphi_R(x,t)$ 、 $\varphi_T(x,t)$ と表した場合、各領域の波動関数は次の通りになります。

$\psi(x,t) =\left\{ \matrix{ \psi_{\rm I}(x,t) &=& \varphi_I(x,t)& +\varphi_R(x,t)& (x<0)\cr \psi_{\rm II}(x,t) &=& \varphi_T(x,t)& & (x\geq 0) } \right.$

入射波の複素振幅を１とした場合の反射波の複素振幅（反射係数）をr、透過波の複素振幅（透過係数）をtとした場合、 $\varphi_I(x,t)$ 、 $\varphi_R(x,t)$ 、 $\varphi_T(x,t)$ は

$\varphi_I(x,t) = e^{ik_{\rm I}x-i\omega t}$
$\varphi_R(x,t) = r(k_{\rm I}) e^{-ik_{\rm I}x-i\omega t}$
$\varphi_T(x,t)= t(k_{\rm I}) e^{ik_{\rm II}x-i\omega t}$

と表すことができます。ポテンシャルの大きさによって波数の大きさは異なるため、それぞれの領域の波数をそれぞれ $k_{\rm I}$ 、 $k_{\rm II}$ とします。エネルギーとポテンシャルとの関係は以下のとおりです。

$k_{\rm I} =\frac{\sqrt{2mE}}{\hbar}$ , $k_{\rm II} =\frac{\sqrt{2m(E-V)}}{\hbar}$

なお、ポテンシャルエネルギーが運動エネルギーを上回る場合（E-V<0）、 $k_{\rm II}$ の平方根が負となるため、純虚数

$k_{\rm II} =\frac{i\sqrt{2m(V-E)}}{\hbar}$

となります。

反射係数と透過係数の与え方

反射係数と透過係数はx=0における境界条件で決定されます。ポテンシャル障壁が有限の高さの場合の境界条件は、２つの領域の波動関数がなめらかに接続するという条件で与えられます。

$\psi_{\rm I}(0,t) = \psi_{\rm II}(0,t)$ 　,　 $\left.\frac{ \partial \psi_{\rm I}(x,t)}{\partial x}\right|_{x=0} = \left.\frac{ \partial \psi_{\rm II}(x,t)}{\partial x}\right|_{x=0}$

この条件から、反射係数と透過係数に関する関係式が

1+r=t , $k_{\rm I}(1-r)= k_{\rm II}\, t$

と導かれるので、これを連立方程式の解として求めると次の通りになります。

$r=\frac{k_{\rm I}-k_{\rm II}}{k_{\rm I}+k_{\rm II}}$ , $t=\frac{2k_{\rm I}}{k_{\rm I}+k_{\rm II}}$

なお、この反射係数と透過係数は運動エネルギーとポテンシャルエネルギーに依存します。

ステップ関数型ポテンシャル障壁へ衝突する波束の運動

先に得られた平面波は波数kが異なっても元のシュレディンガー方程式を満たすため、無限に高いポテンシャル障壁が存在する場合でも、平面波の重ね合わせで波束の運動を調べることができます。異なる波数（角振動数）をもつ平面波を次のとおりに表します。

$\psi_{\rm I}(x,t)= \frac{1}{\sqrt{L}} \sum\limits_{n}c_n \left[e^{ik_{{\rm I}n}x}+r_n e^{-ik_{{\rm I}n}x}\right] e^{-i\omega_n t}$
$\psi_{\rm II}(x,t)= \frac{1}{\sqrt{L}} \sum\limits_{n}c_n \left[t_ne^{ik_{{\rm II}n}x}\right] e^{-i\omega_n t}$

ただし、エネルギーと角振動数、波数の関係性（分散関係）は以下のとおりです。

$E_n=\hbar\omega_n=\frac{\hbar^2k_{n}^2}{2m}$ , $k_{{\rm I}n} =\frac{\sqrt{2m(E_n-V_{\rm I})}}{\hbar}$ , $k_{{\rm II}n} =\frac{\sqrt{2m(E_n-V_{\rm II})}}{\hbar}$

シミュレーション結果

初期状態として左から右向きに運動する波束の運動です。

計算パラメータ

波束の中心エネルギー：E0 = 10.0 * eV;
空間スケール 1E-11[m];//横軸の値
時間スケール 1E-16[s];//動画１コマの時間間隔

V<0の場合

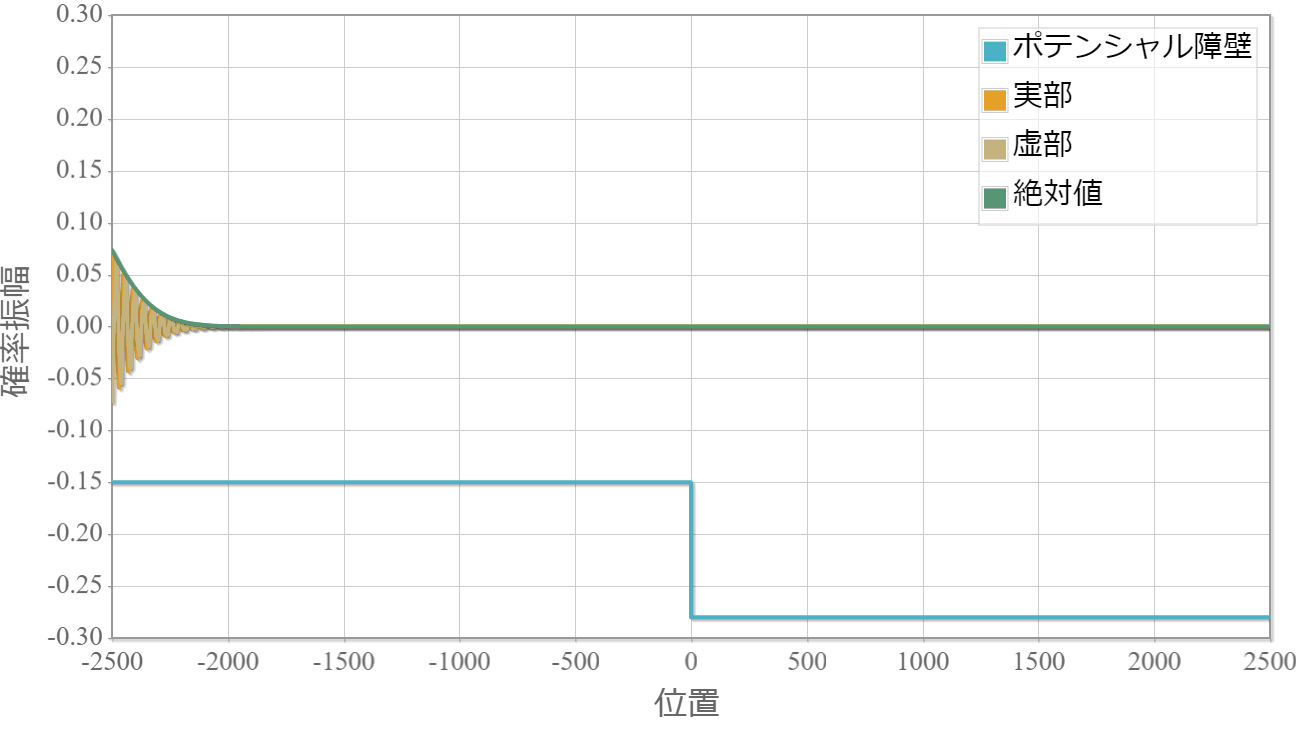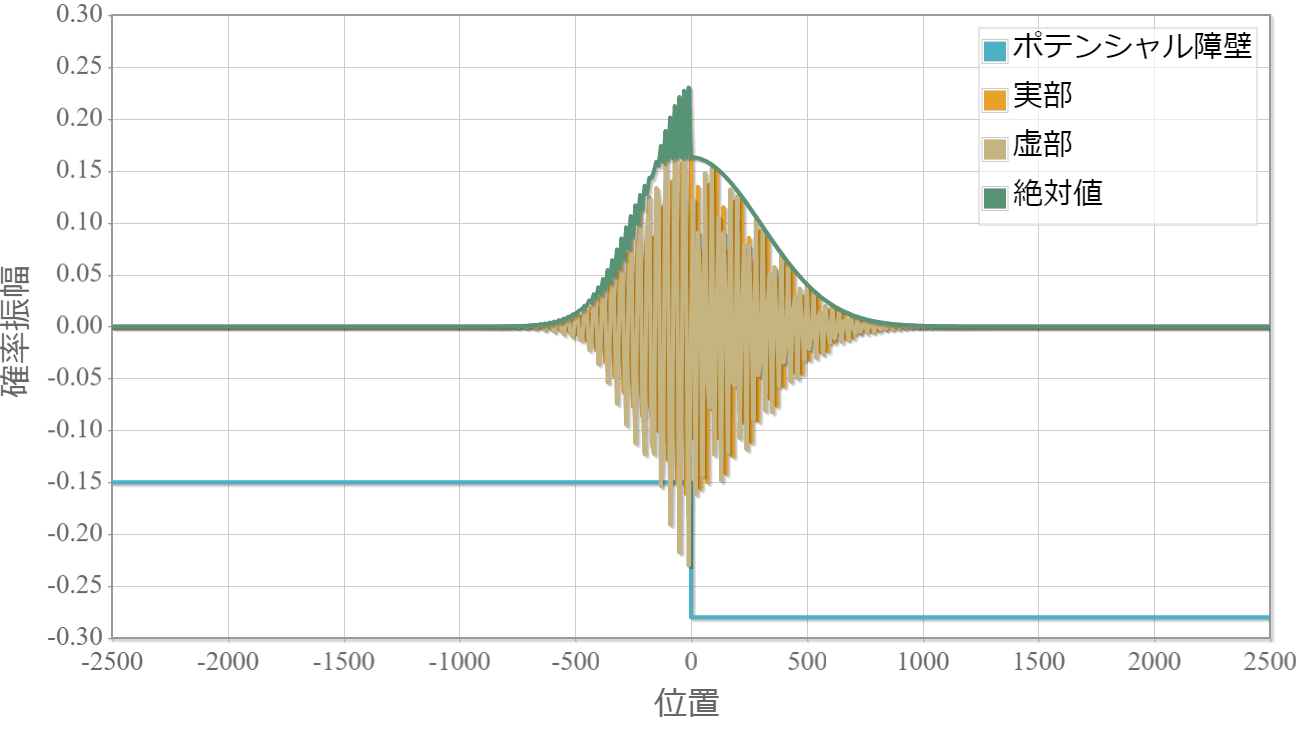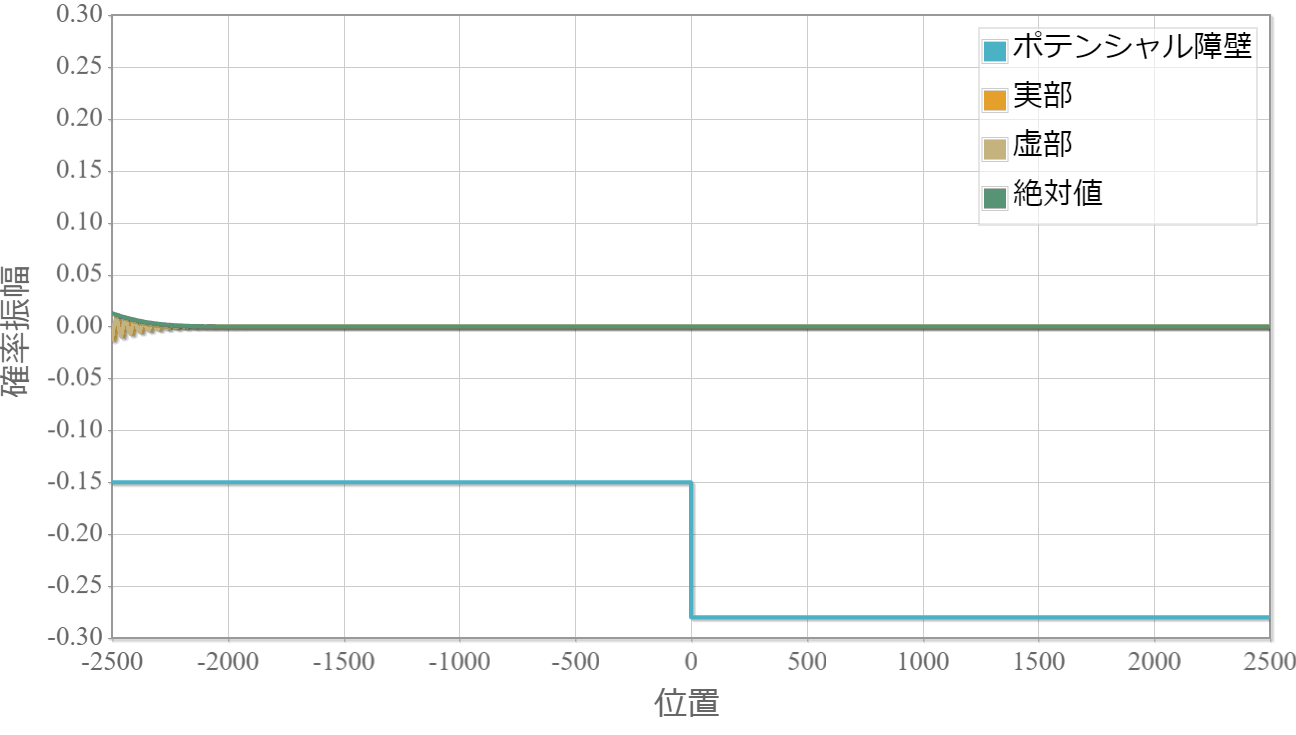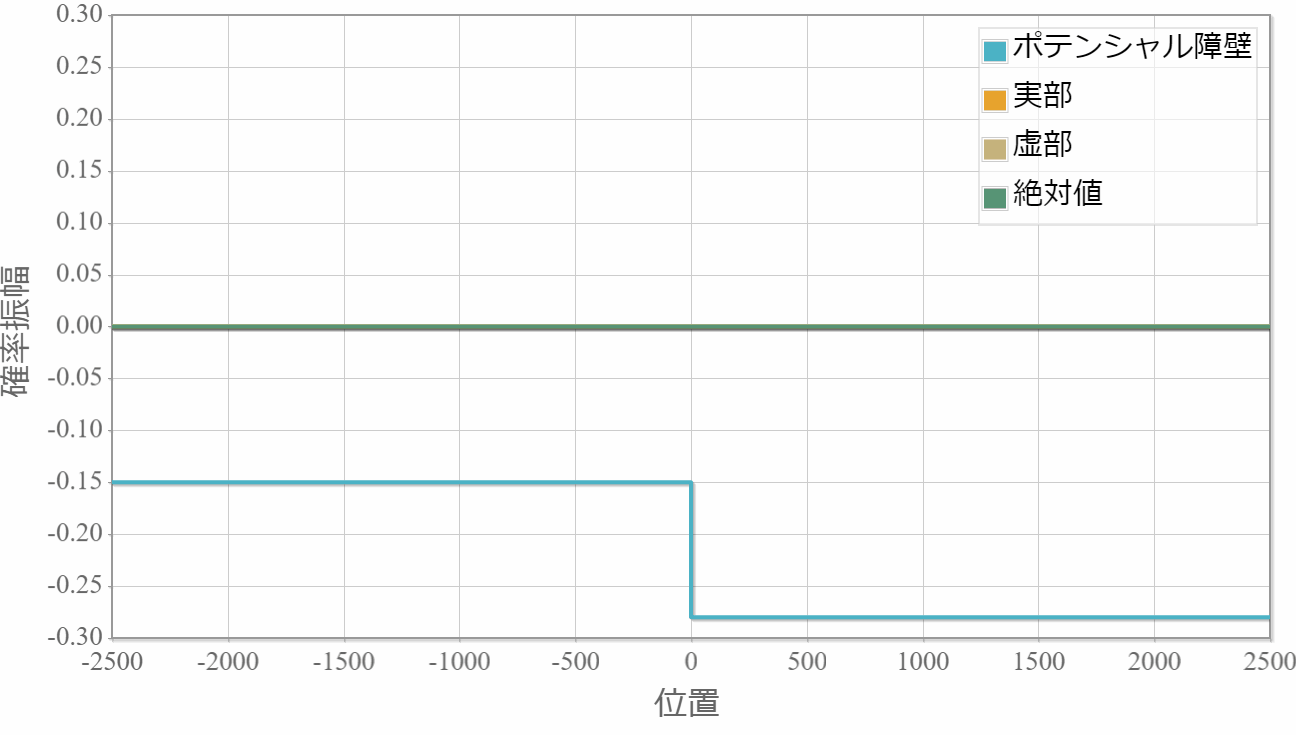
ポテンシャル障壁の高さが負の場合でも反射が存在します。

考察と次の課題

・無限にステップ関数型ポテンシャル障壁への衝突は問題ないようだ
・次はデルタ関数型ポテンシャル障壁への衝突をシミュレーションしてみます。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics4.cpp
※VisualC++、GCC（MinGW）で動作確認しています。

	MEMSパークコンソーシアム設立20周年記念シンポジウムにおいて「国際イノベーションコンテスト」世界１位入賞アプリを展示しました 2024.12.29 【大草芳江｜TOPICS】
	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】

【量子力学再入門4】
ステップ関数型ポテンシャルへの衝突

対象とする系：ステップ関数型ポテンシャル障壁へ衝突する量子粒子

ステップ関数型ポテンシャルの定義

ステップ関数型ポテンシャル障壁へ衝突する平面波解

反射係数と透過係数の与え方

ステップ関数型ポテンシャル障壁へ衝突する波束の運動

シミュレーション結果

計算パラメータ

V<0の場合

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門4】ステップ関数型ポテンシャルへの衝突

対象とする系：ステップ関数型ポテンシャル障壁へ衝突する量子粒子

ステップ関数型ポテンシャルの定義

ステップ関数型ポテンシャル障壁へ衝突する平面波解

反射係数と透過係数の与え方

ステップ関数型ポテンシャル障壁へ衝突する波束の運動

シミュレーション結果

計算パラメータ

V<0の場合

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門4】
ステップ関数型ポテンシャルへの衝突