【ルンゲ・クッタで行こう！】
放物運動シミュレーション

当方、最近の興味は物理シミュレーションとニューラルネットワークを組み合わせたある種の最適化問題を解くことを目的としています。その準備として、簡単な物理系の数値計算の動作チェックを行います。

放物運動シミュレーション

地上で物体を斜めに投射（斜方投射）すると、物体は放物線状の軌跡を描いて飛んでいきます。地上には空気が存在するために、物体には運動を阻害する抵抗力（空気抵抗）が加わるため、この放物線状の軌跡は完全な放物線（２次関数）にはなりません。この空気抵抗力が加わった物体の加速度ベクトル は、次のとおりに与えられます。

重力＋空気抵抗力による物体の加速度ベクトル

は物体の速度ベクトル、mは物体の質量、 は重力加速度ベクトル、 は粘性抵抗係数と呼ばれる空気抵抗力の大きさを表す定数です。この表式は速度の大きさに比例して反対向きの力（空気抵抗力）が大きくなる結果、加速度が小さくなることを表しています。

空気抵抗力が存在する斜方投射の計算結果

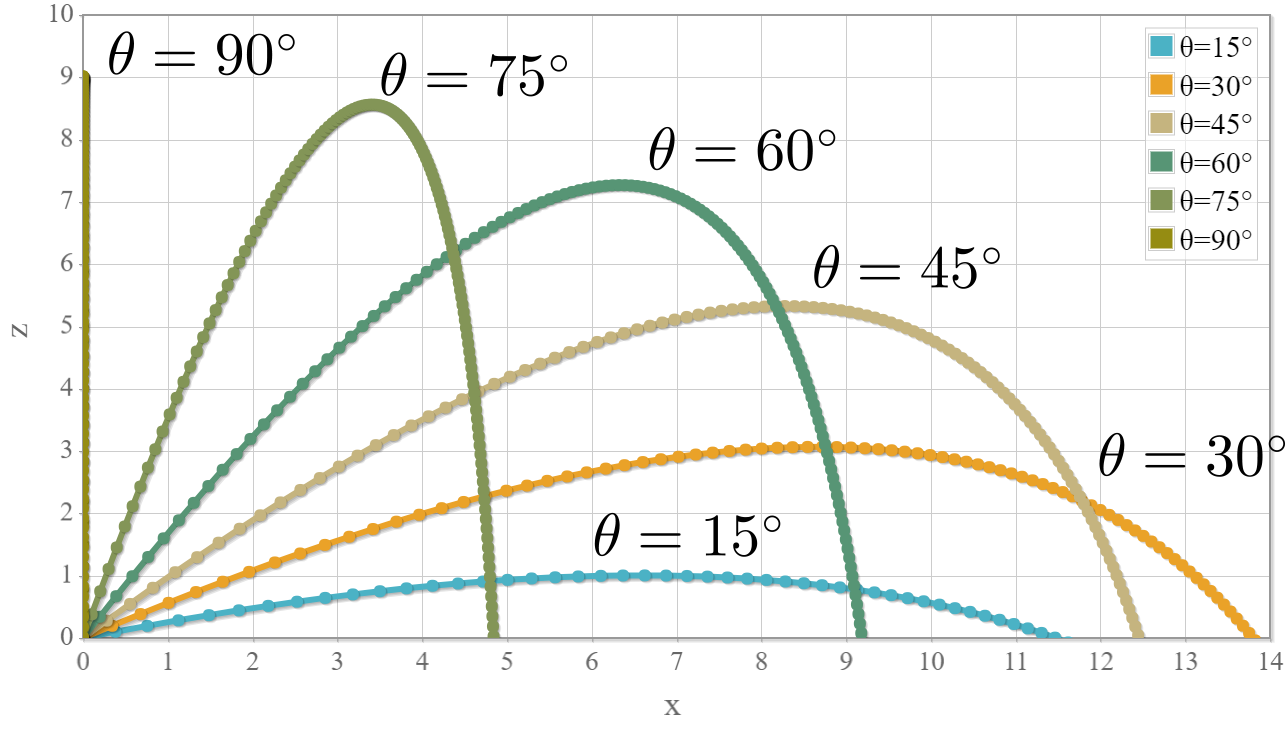
次のグラフは先の加速度ベクトルを用いて空気抵抗力が存在する斜方投射を計算した結果です。初速度20[m/s]で様々な投射角度（）で投射しています。その他のパラメータは 、 、 です。空気抵抗力が存在しない場合には が最も遠くに飛びますが、空気抵抗力が存在する場合の到達距離が最大となる投射角度はとなります。

考察と次の課題

・空気抵抗力が存在する放物運動の軌跡は正しく計算できました。
・空気抵抗力が存在する放物運動の軌跡は特別な場合を除いて解析的に表すことができません。この軌跡をニューラルネットワークで学習することを行ってみます。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/NN/ProjectileMotion_AirResistance_RK4.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。

参考

上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。数値計算の方法などは 「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～」を参照ください。