【量子力学再入門5】
デルタ関数型ポテンシャルへの衝突

文責：遠藤理平（2018年4月28日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。５回目のテーマは「デルタ関数型ポテンシャル障壁への衝突」です。

デルタ関数型ポテンシャル障壁とは

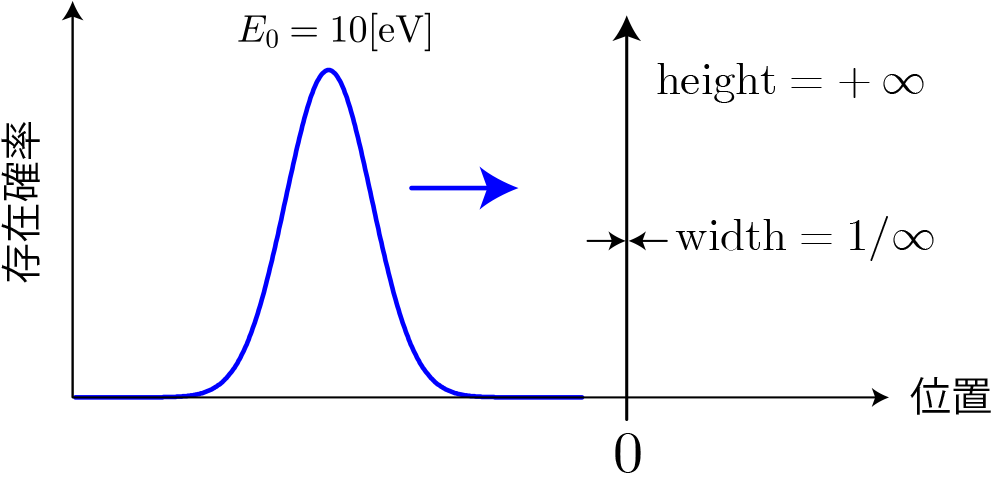
今回のデルタ型ポテンシャル障壁とは、面積を１に固定したまま高さを無限大、幅を無限小の極限としたポテンシャル障壁を指します。ポテンシャル障壁は無限大に高いですが、無限小に薄いために量子粒子の一部は透過します。このようなデルタ関数型ポテンシャル障壁が存在する系でもそれぞれの領域で存在しうる平面波の重ね合わせで波束の運動をシミュレーションすることができます。デルタ関数型ポテンシャルの定義

デルタ関数型ポテンシャルの定義

$V(x)= V_0\delta(x)$

デルタ関数の定義

デルタ関数を実現する関数形は複数ありますが、原点を含む領域の積分で定義される次式は具体的な関数形を必要としません。

$\int _{-\infty}^{\infty}f(x)\delta(x)dx=f(0)$

平面波解

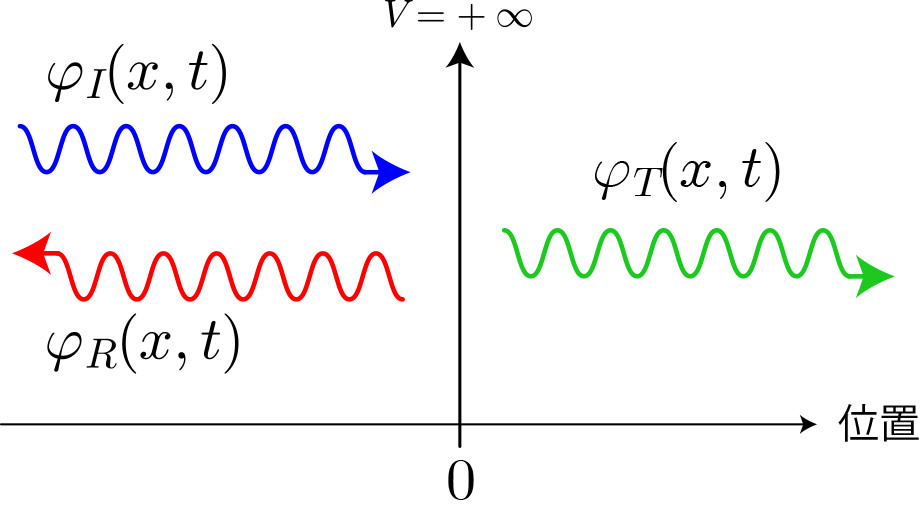
図はx<0とx≧0の領域における単一平面波の模式図です。入射波、反射波、透過波の波動関数をそれぞれ $\varphi_I(x,t)$ 、 $\varphi_R(x,t)$ 、 $\varphi_T(x,t)$ と表した場合、各領域の波動関数は次の通りになります。

$\psi(x,t) =\left\{ \matrix{ \psi_{\rm I}(x,t) = \varphi_I(x,t) +\varphi_R(x,t)& (x<0)\cr \psi_{\rm II}(x,t) = \varphi_T(x,t) \ \ \ \ \ \ \ \ \ \, & (x\geq 0) } \right.$

入射波の複素振幅を１とした場合の反射波の複素振幅（反射係数）をr、透過波の複素振幅（透過係数）をtとした場合、 $\varphi_I(x,t)$ 、 $\varphi_R(x,t)$ 、 $\varphi_T(x,t)$ は

$\varphi_I(x,t) = e^{ikx-i\omega t}$
$\varphi_R(x,t) = r(k) e^{-ikx-i\omega t}$
$\varphi_T(x,t)= t(k) e^{ikx-i\omega t}$

と表すことができます。

反射係数と透過係数の与え方

反射係数と透過係数はx=0における境界条件で決定されます。ポテンシャル障壁がデルタ関数型の場合、２つの領域の波動関数は連続

$\psi_{\rm I}(0,t) = \psi_{\rm II}(0,t)$

である必要はあるが、デルタ関数型のポテンシャルの影響でなめらかに接続するかどうかは自明ではありません。この接続条件を元のシュレディンガー方程式

$-\frac{\hbar^2}{2m}\, \frac{d^2 \varphi(x)}{dx^2} +V_0\delta(x) \varphi(x) = E \varphi(x)$

から導出します。デルタ関数の性質を利用するために、両辺を原点を含む微小領域で積分を行います。

$- \frac{\hbar^2}{2m}\int_{-\Delta}^{\Delta} \frac{d^2 \varphi(x)}{dx^2} dx +\int_{-\Delta}^{\Delta} V_0\delta(x) \varphi(x)dx = E \int_{-\Delta}^{\Delta}\varphi(x)dx$

この $\Delta$ を0へ極限をとると右辺の波動関数単体の積分は０に収束します。原点への＋側からの収束と－側からの収束を考慮すると、波動関数の傾きに関する条件する条件は次のとおり与えられます。

$- \frac{\hbar^2}{2m}\left[ \left.\frac{d \varphi(x)}{dx}\right|_{x=+0} - \left.\frac{d \varphi(x)}{dx}\right|_{x=-0} \right] + V_0\varphi(0) = 0$
$\left.\frac{d \varphi_{\rm II}(x)}{dx}\right|_{x=0} = \left.\frac{d \varphi_{\rm I}(x)}{dx}\right|_{x=0} + \frac{2mV_0}{\hbar^2}\,\varphi(0)$

連続と傾きの条件から、反射係数と透過係数に関する２つの方程式は

1+r=t
$k (1-r)= (k- \frac{2mV_0}{\hbar^2} )\, t$

となり、これを連立方程式の解として求めると次の通りになります。

$r = -\frac{ \frac{2mV_0}{\hbar^2}}{2k -\frac{2mV_0}{\hbar^2}}$ , $t = \frac{ 2k }{2k -\frac{2mV_0}{\hbar^2}}$

なお、この反射係数と透過係数は運動エネルギーとポテンシャルエネルギーに依存します。

シミュレーション結果

初期状態として左から右向きに運動する波束の運動です。

計算パラメータ

デルタ関数の高さ: V0 = 1E-9[J]
波束の中心エネルギー：E0 = 10.0 * eV;
空間スケール 1E-11[m];//横軸の値
時間スケール 1E-16[s];//動画１コマの時間間隔

考察と次の課題

・デルタ関数型ポテンシャル障壁への衝突は問題ないようだ
・次は箱型ポテンシャル障壁への衝突をシミュレーションしてみます。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics4.cpp
※VisualC++、GCC（MinGW）で動作確認しています。

	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】
	「natural science 科学・技術講座」講師３人で設立した株式会社weCAN。アイディアの商品化第一弾「美姿勢メガネ」を朝日新聞さんに取材いただきました。 2021.08.23 【遠藤理平｜パブリシティ】

【量子力学再入門5】
デルタ関数型ポテンシャルへの衝突

デルタ関数型ポテンシャル障壁とは

デルタ関数型ポテンシャルの定義

デルタ関数の定義

平面波解

反射係数と透過係数の与え方

シミュレーション結果

計算パラメータ

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門5】デルタ関数型ポテンシャルへの衝突

デルタ関数型ポテンシャル障壁とは

デルタ関数型ポテンシャルの定義

デルタ関数の定義

平面波解

反射係数と透過係数の与え方

シミュレーション結果

計算パラメータ

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門5】
デルタ関数型ポテンシャルへの衝突