【量子力学再入門6】
箱型ポテンシャル障壁への衝突（転送行列法による振幅計算方法の解説）

文責：遠藤理平（2018年5月 2日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。６回目のテーマは「箱型ポテンシャル障壁への衝突」です。

箱型ポテンシャル障壁とは

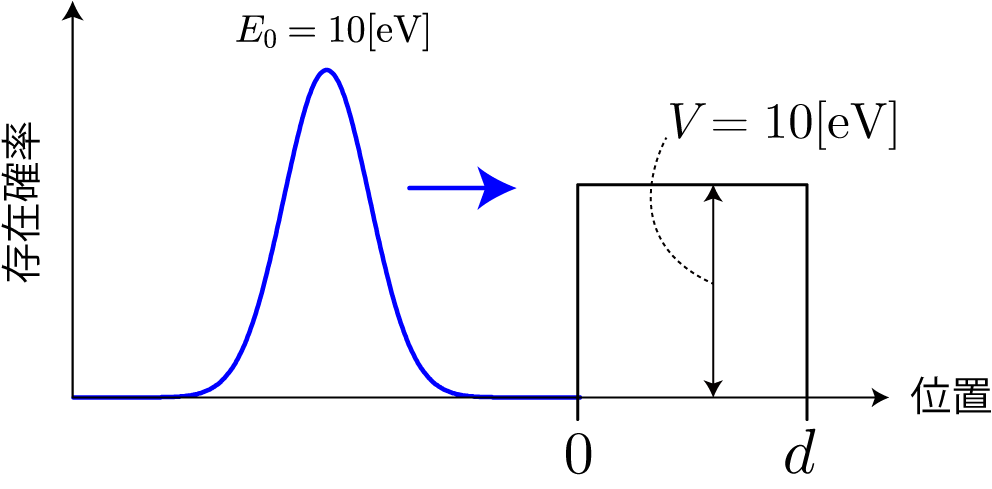
今回の箱型ポテンシャル障壁とはある区間だけポテンシャルが存在する系を表します。このような箱型ポテンシャル障壁が存在する系でもそれぞれの領域で存在しうる平面波の重ね合わせで波束の運動をシミュレーションすることができます。

箱型ポテンシャルの定義

$V(x) =\left\{ \matrix{ V_{\rm I} & (x<0) \cr V_{\rm II} & (0\le x<d) \cr V_{\rm III} & (d\le x)} \right.$

平面波解

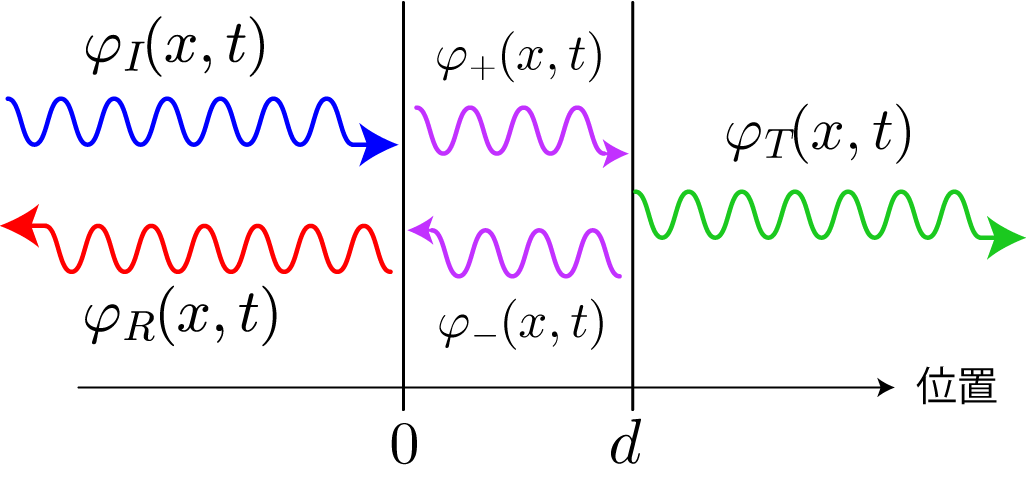
３つの領域における単一平面波の模式図です。入射波、反射波、透過波の波動関数をそれぞれ $\varphi_I(x,t)$ 、 $\varphi_R(x,t)$ 、 $\varphi_T(x,t)$ と表し、 $0\le x<d$ の前進波と後進波の波動関数をそれぞれ $\varphi_+(x,t)$ 、 $\varphi_-(x,t)$ と表した場合、各領域の波動関数は次の通りになります。

$\psi_{\rm I}(x,t) = \varphi_I(x,t) +\varphi_R(x,t) = \left[ e^{ik_{\rm I}x} +re^{-ik_{\rm I}x}\right] e^{-i\omega t}$
$\psi_{\rm II}(x,t) = \varphi_{+}(x,t) +\varphi_{-}(x,t)= \left[Ae^{ik_{\rm II}x} +Be^{-ik_{\rm II}x}\right] e^{-i\omega t}$
$\psi_{\rm III}(x,t) = \varphi_T(x,t) = \left[te^{ik_{\rm III}(x-d)} \right] e^{-i\omega t}$

これらの未知の係数 r, t, A, B は各領域間でなめらかに接続する条件（連続条件と傾きが連続する条件）

$\psi_{\rm I}(0,t) = \psi_{\rm II}(0,t)$ , $\psi_{\rm II}(d,t) = \psi_{\rm III}(d,t)$
$\left.\frac{ \partial \psi_{\rm I}(x,t)}{\partial x}\right|_{x=0} = \left.\frac{ \partial \psi_{\rm II}(x,t)}{\partial x}\right|_{x=0}$ , $\left.\frac{ \partial \psi_{\rm II}(x,t)}{\partial x}\right|_{x=d} = \left.\frac{ \partial \psi_{\rm III}(x,t)}{\partial x}\right|_{x=d}$

から決定することができます。これらから得られる方程式は次のとおりです。

1+r= A+B
$Ae^{ik_{\rm II}d} +Be^{-ik_{\rm II}d} =t$
$k_{\rm I}(1-r)= k_{\rm II}(A-B)$
$k_{\rm II} \left[ Ae^{ik_{\rm II}d} -Be^{-ik_{\rm II}d} \right] =k_{\rm III} t$

この連立方程式を解いて、先の表式に代入することで波動関数を得ることもできますが、本項では任意の層状ポテンシャルの系に適用することのできるより一般的な方法「転送行列法」を紹介します。

転送行列法による解法

転送行列法とは、波動方程式から得られる境界条件から領域間の波動関数の関係を表現する行列を導出し、後はその行列の積で層状の媒質中の波の伝搬の様子を調べる一般的な手法と確立しています。シュレディンガー方程式も波動方程式なので適用することができます。なお、転送行列は（１）境界面を表す行列と（２）各領域両端の振幅の関係を表す行列の２つで構成されます。

（１）境界面を表す行列

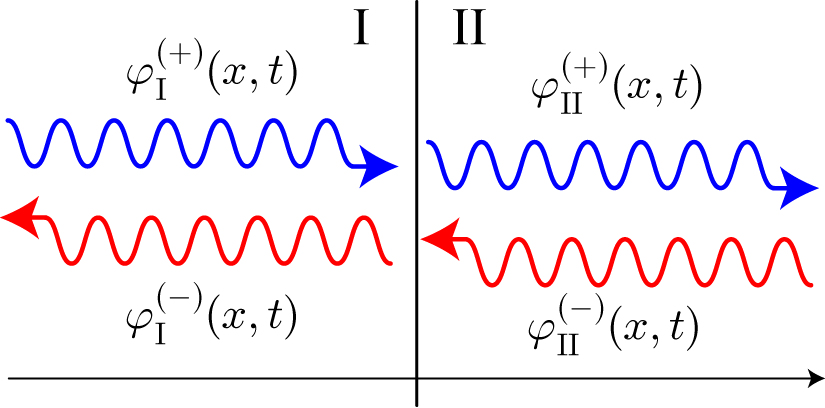
図は領域Iと領域IIにおける前進波と後進波を表す模式図です。領域Iと領域IIのはどう関数はそれぞれ前進波と後進波の和で表すことができ、ハミルトニアンが時間に依存しない場合には次のとおり表すことができます。

$\psi_{\rm I}(x,t) = \varphi_{\rm I}^{(+)}(x,t) +\varphi_{\rm I}^{(-)}(x,t) = \left[ A_{\rm I}^{(+)} e^{ik_{\rm I}x} + A_{\rm I}^{(-)} e^{-ik_{\rm I}x} \right]e^{-i\omega t}$
$\psi_{\rm II}(x,t) = \varphi_{\rm II}^{(+)}(x,t) +\varphi_{\rm II}^{(-)}(x,t) = \left[ A_{\rm II}^{(+)} e^{ik_{\rm II}x} + A_{\rm II}^{(-)} e^{-ik_{\rm II}x} \right]e^{-i\omega t}$

なお、x=0が境界と想定していますが、境界の座標を $x= x_{\rm I, II}$ に拡張する場合は、指数部のxを $x-x_{\rm I, II}$ に置き換える形で対応することができます。各領域の波動関数の前進波と後進波の４つの係数はこれまでと同様、なめらかに連続する条件

$\psi_{\rm I}(0,t) = \psi_{\rm II}(0,t)$
$\left.\frac{ \partial \psi_{\rm I}(x,t)}{\partial x}\right|_{x=0} = \left.\frac{ \partial \psi_{\rm II}(x,t)}{\partial x}\right|_{x=0}$

から導くことができます。具体的な方程式は次のとおりです。

$A_{\rm I}^{(+)} + A_{\rm I}^{(-)}=A_{\rm II}^{(+)} + A_{\rm II}^{(-)}$
$k_{\rm I} \left(A_{\rm I}^{(+)} - A_{\rm I}^{(-)}\right) = k_{\rm II} \left(A_{\rm II}^{(+)} - A_{\rm II}^{(-)}\right)$

これらを整理すると、領域Iと領域IIの係数の関係を導くことができます。

$A_{\rm II}^{(+)}=\frac{1}{2} \left[ \left( 1+\frac{k_{\rm I}}{k_{\rm II}} \right) A_{\rm I}^{(+)} + \left( 1-\frac{k_{\rm I}}{k_{\rm II}} \right) A_{\rm I}^{(-)}\right]$
$A_{\rm II}^{(-)}=\frac{1}{2} \left[ \left( 1-\frac{k_{\rm I}}{k_{\rm II}} \right) A_{\rm I}^{(+)} + \left( 1+\frac{k_{\rm I}}{k_{\rm II}} \right) A_{\rm I}^{(-)}\right]$

各領域の振幅を縦ベクトルとして行列に表したのが次の式です。

$\left(\matrix{ A_{{\rm II}}^{(+)}\cr A_{{\rm II}}^{(-)}} \right) =$ $\frac{1}{2} \left( \matrix{ 1+\frac{k_{\rm I}}{k_{\rm II}} & 1-\frac{k_{\rm I}}{k_{\rm II}} \cr 1-\frac{k_{\rm I}}{k_{\rm II}} & 1+\frac{k_{\rm I}}{k_{\rm II}} } \right)$ $\left(\matrix{ A_{{\rm I}}^{(+)}\cr A_{{\rm I}}^{(-)}} \right)$
$A_{{\rm II}}=M_{\rm II, I} A_{{\rm I}}$

ちなみに、 $M_{\rm II, I}$ の添字を入れ替えた $M_{\rm I, II}$ は反対に領域IIを基準とした領域Iの振幅を表わしますが、これは $M_{\rm II, I}$ の逆行列と一致します。

$M_{\rm I, II} = M_{\rm II, I}^{-1} =$ $\frac{1}{2} \left( \matrix{ 1+\frac{k_{\rm II}}{k_{\rm I}} & 1-\frac{k_{\rm II}}{k_{\rm I}} \cr 1-\frac{k_{\rm II}}{k_{\rm I}} & 1+\frac{k_{\rm II}}{k_{\rm I}} } \right)$

つまり、境界面における振幅の関係はこの行列１つで表すことができ、例えば、領域IIとIIIの関係がほしければ、添字のIとIIをそれぞれIIをIIIへ書き換えることでそのまま成り立ちます。

（２）境界面を表す行列

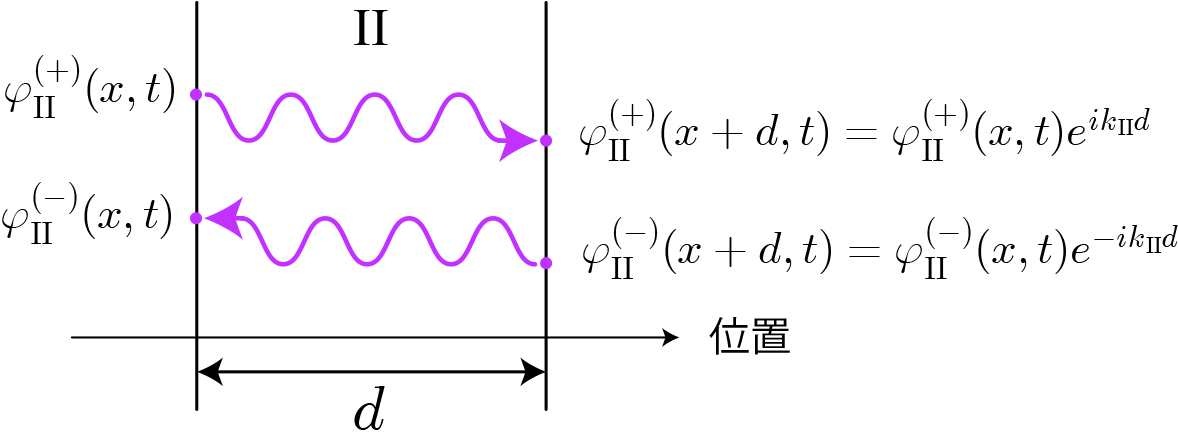
続いて、領域II両端の前進波と後進波の振幅の関係を表す行列を示します。領域内では通常の平面波なので、振幅の違いは空間移動による位相変化分となります。これを行列に表したのが次式です。

$\left(\matrix{ \varphi_{{\rm II}}^{(+)}(x+d,t)\cr \varphi_{{\rm II}}^{(-)}(x+d,t) }\right) =$ $\left( \matrix{ e^{ik_{\rm II}d} & 0 \cr 0 & e^{-ik_{\rm II}d} } \right) \left(\matrix{ \varphi_{{\rm II}}^{(+)}(x,t)\cr \varphi_{{\rm II}}^{(-)}(x,t) }\right)$

つまり、領域IIの左端の進行波と後進波の振幅を１とした場合の右端の振幅を表す行列は

$T_{\rm II}= \left( \matrix{ e^{ik_{\rm II}d} & 0 \cr 0 & e^{-ik_{\rm II}d} } \right)$

となります。

領域Iと領域IIIの振幅をつなぐ転送行列

以上の結果を踏まえて、領域Iと領域IIIの振幅をつなぐ転送行列は、領域Iと領域IIつなぐ $M_{\rm II, I}$ 、領域IIの両端をつなぐ $T_{\rm II}$ 、領域IIと領域IIIをつなぐ $M_{\rm III, II}$ を順番に積算した

$\left(\matrix{ A_{{\rm III}}^{(+)}\cr A_{{\rm III}}^{(-)}} \right) =$ $M_{\rm III, II} \, T_{\rm II} M_{\rm II, I}\left(\matrix{ A_{{\rm I}}^{(+)}\cr A_{{\rm I}}^{(-)}} \right)=$ $M_{\rm III, I}\left(\matrix{ A_{{\rm I}}^{(+)}\cr A_{{\rm I}}^{(-)}} \right)$

と表すことができます $M_{\rm III, I}$ が領域Iと領域IIIをつなぐ転送行列です。この行列は先に定義した２種類の行列を積算することで求めることができます。

反射係数と透過係数の求め方

この $M_{\rm III, I}$ から反射係数と透過係数を計算する方法を示します。領域がI, II, IIIの３領域で、領域I方向から入射する場合、 $A_{{\rm III}}^{(-)}}$ は存在しないため、必ず０となります。そのため、 $M_{\rm III, I}$ の行列要素を $m_{11}, m_{12}, m_{21}, m_{22}$ と表すと

$\left(\matrix{ A_{{\rm III}}^{(+)}\cr 0} \right) = \left( \matrix{ m_{11} & m_{12} \cr m_{21} & m_{22} } \right) \left(\matrix{ A_{{\rm I}}^{(+)}\cr A_{{\rm I}}^{(-)}} \right)$

となります。この行列化から

$0= m_{21}A_{{\rm I}}^{(+)} + m_{22}A_{{\rm I}}^{(-)}$
$A_{{\rm III}}^{(+)} = m_{11}A_{{\rm I}}^{(+)} + m_{12}A_{{\rm I}}^{(-)}$

と計算できるので、これから反射係数、透過係数と行列要素の関係式が得られます。

$r=\frac{A_{{\rm I}}^{(-)}}{A_{{\rm I}}^{(+)}} = -\frac{m_{21}}{m_{22}}$
$t= \frac {A_{{\rm III}}^{(+)}}{A_{{\rm I}}^{(+)}}=m_{11}- \frac {m_{12}m_{21}}{m_{22}}=\frac{ m_{11}m_{22}-m_{12} m_{21}}{m_{22}}=\frac{ \det(M_{\rm III, I}) }{m_{22}}$

つまり、転送行列を計算した後に、その行列要素から直接、反射係数と透過係数を計算することができます。さらに、rを計算した後に領域IIの振幅は領域Iと領域IIの関係を表す行列から直ちに

$\left(\matrix{ A_{{\rm II}}^{(+)}\cr A_{{\rm II}}^{(-)}} \right) = M_{\rm II, I}$ $\left(\matrix{ 1\cr r} \right)$

と計算することができます。以上で全領域の波動関数を計算することができました。

$\psi_{\rm I}(x,t) = \left[ e^{ik_{\rm I}x} +re^{-ik_{\rm I}x}\right] e^{-i\omega t}$
$\psi_{\rm II}(x,t) = \left[A_{\rm II}^{(+)}e^{ik_{\rm II}x} +A_{\rm II}^{(-)}e^{-ik_{\rm II}x}\right] e^{-i\omega t}$
$\psi_{\rm III}(x,t) = \left[te^{ik_{\rm III}(x-d)} \right] e^{-i\omega t}$

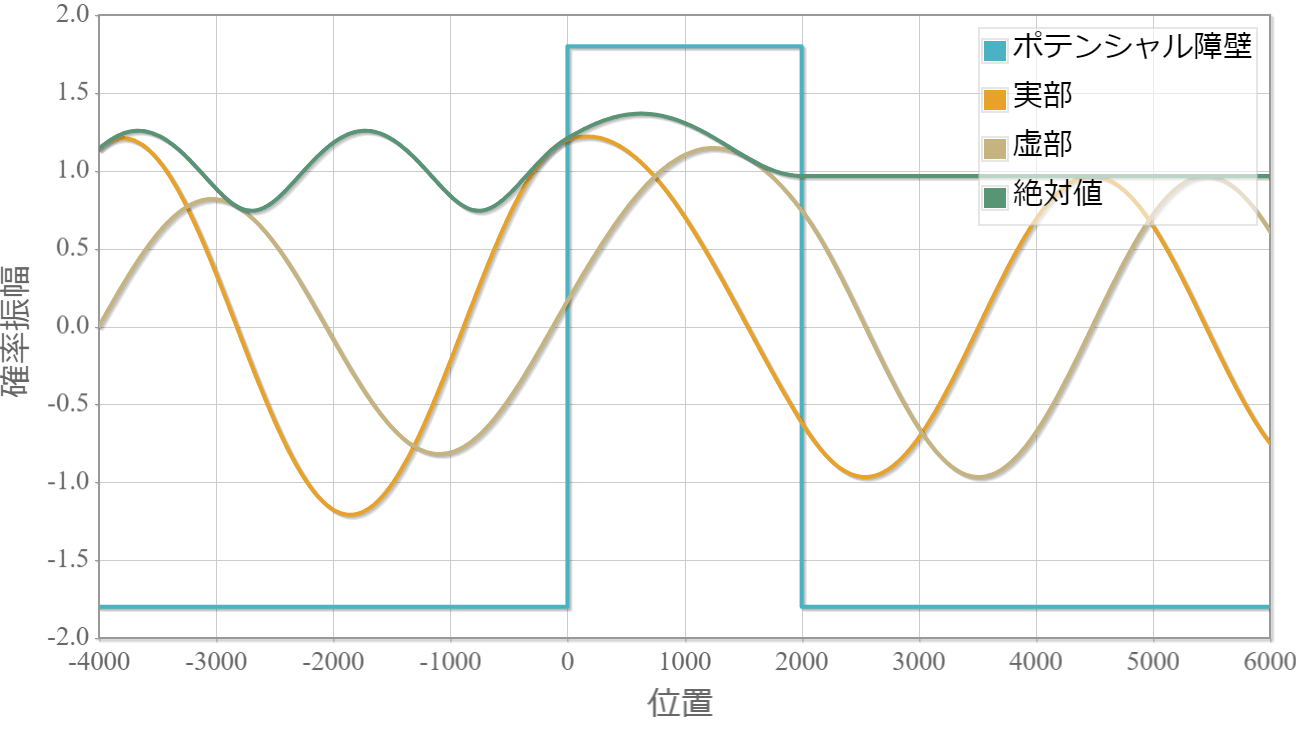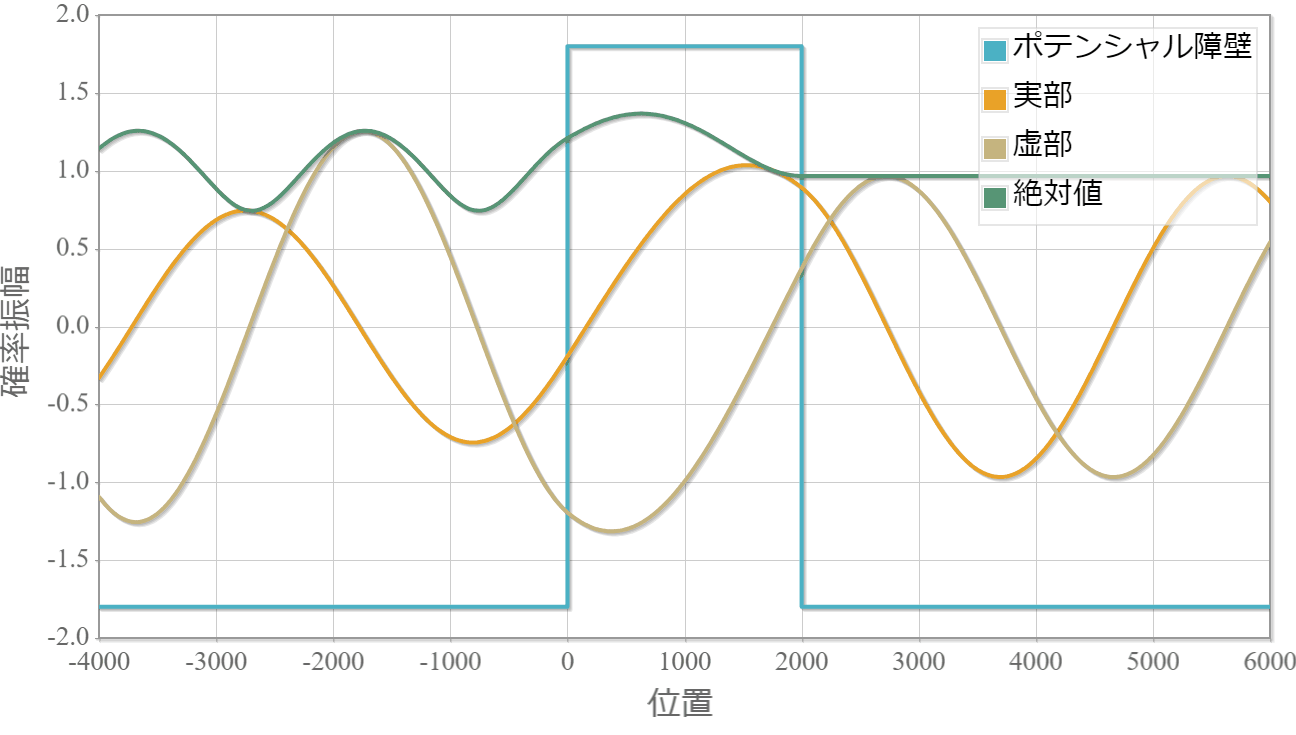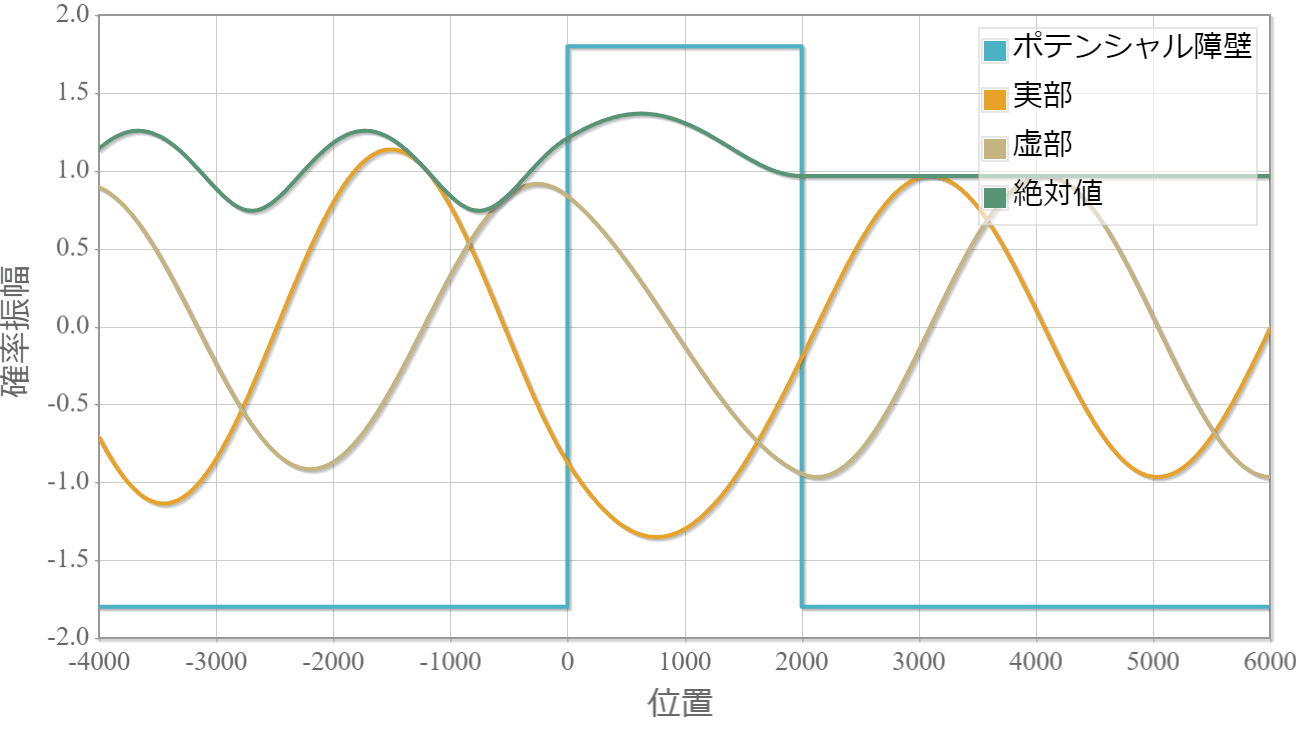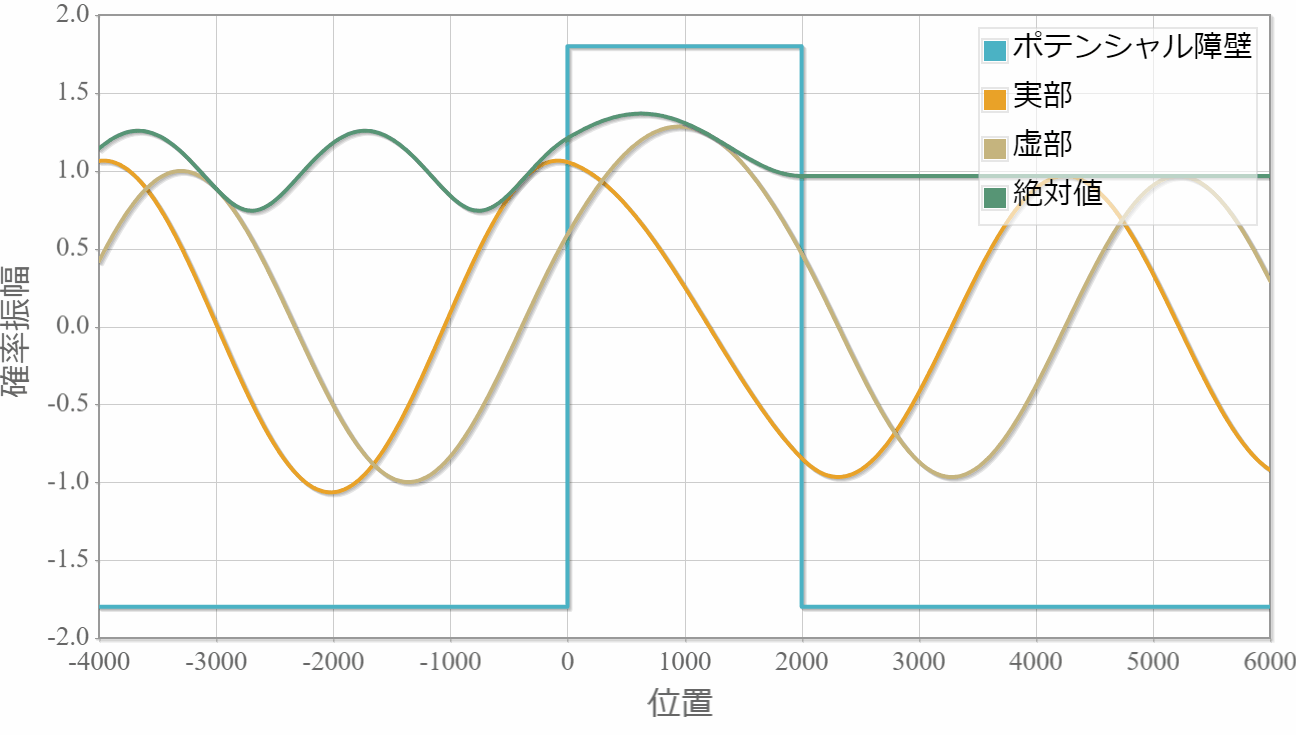
シミュレーション結果

箱型ポテンシャル障壁に衝突する単一平面波の様子です。左より入射してます。

計算パラメータ

ポテンシャルの高さ: V2 = 5.0 * eV
平面波のエネルギー：E0 = 10.0 * eV;
空間スケール 1E-13[m];//横軸の値

考察と次の課題

・境界面でもなめらかに接続する様子がわかります。
・絶対値が時間に依存しないのは定常解であるためです。
・次は波束を箱型ポテンシャル障壁へ衝突させます。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics6.cpp
※VisualC++、GCC（MinGW）で動作確認しています。

	MEMSパークコンソーシアム設立20周年記念シンポジウムにおいて「国際イノベーションコンテスト」世界１位入賞アプリを展示しました 2024.12.29 【大草芳江｜TOPICS】
	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】

【量子力学再入門6】
箱型ポテンシャル障壁への衝突（転送行列法による振幅計算方法の解説）

箱型ポテンシャル障壁とは

箱型ポテンシャルの定義

平面波解

転送行列法による解法

（１）境界面を表す行列

（２）境界面を表す行列

領域Iと領域IIIの振幅をつなぐ転送行列

反射係数と透過係数の求め方

シミュレーション結果

計算パラメータ

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門6】箱型ポテンシャル障壁への衝突（転送行列法による振幅計算方法の解説）

箱型ポテンシャル障壁とは

箱型ポテンシャルの定義

平面波解

転送行列法による解法

（１）境界面を表す行列

（２）境界面を表す行列

領域Iと領域IIIの振幅をつなぐ転送行列

反射係数と透過係数の求め方

シミュレーション結果

計算パラメータ

考察と次の課題

プログラムソース（C++）

関連記事

仮想物理実験室

計算物理学

Ranking アクセスランキング

【量子力学再入門6】
箱型ポテンシャル障壁への衝突（転送行列法による振幅計算方法の解説）