【量子力学再入門7】
箱型ポテンシャル障壁によるトンネル効果
量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。 メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。本項では量子力学の基本的な問題を数値的に解くことで、量子力学の理解を深めることが目的とします。7回目のテーマは「箱型ポテンシャル障壁によるトンネル効果」です(波束の箱型ポテンシャル障壁への衝突は次回行います)。
箱型ポテンシャル障壁によるトンネル効果とは
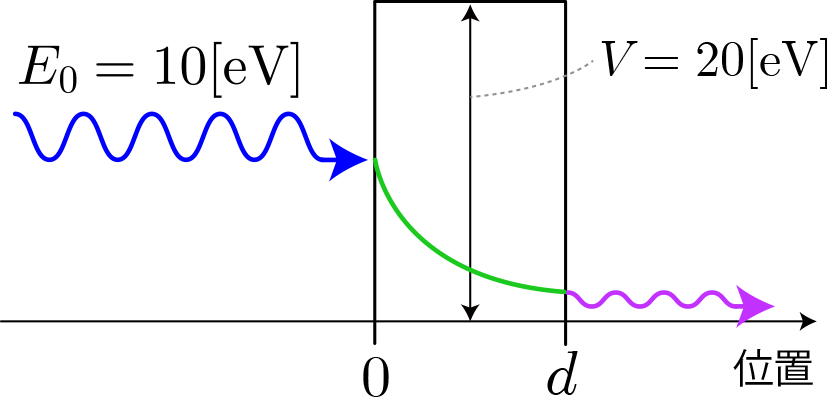
古典力学で対象とする質点の運動において、物体が持っている力学的エネルギー(運動エネルギー+ポテンシャルエネルギー)よりも大きなポテンシャル障壁が存在する場合、外からの力が加わらない限りその障壁を越えることはありません。しかしながら、波の場合には禁止された領域に染み出すことは様々な物理系で実験的にも理論的にも認められています。最も有名な例は光が境界面で全反射する際に反対側に染み出すエバネッセント光です。この現象は、波動現象一般で生じるため、波動方程式であるシュレディンガー方程式の解にも存在します。
トンネル効果とは量子力学的粒子が持つ運動エネルギーよりも大きなポテンシャル障壁が存在する系にて、ポテンシャル障壁を突き抜ける現象を指します。
ポテンシャル障壁中の波動関数
ポテンシャル障壁中の波動関数は前項で示したとおり、
です。量子力学的粒子の運動エネルギーがポテンシャル障壁の大きさよりも小さい場合、量子力学的粒子の波数が純虚数となります。つまり、
とおいて、波動関数は
シミュレーション結果
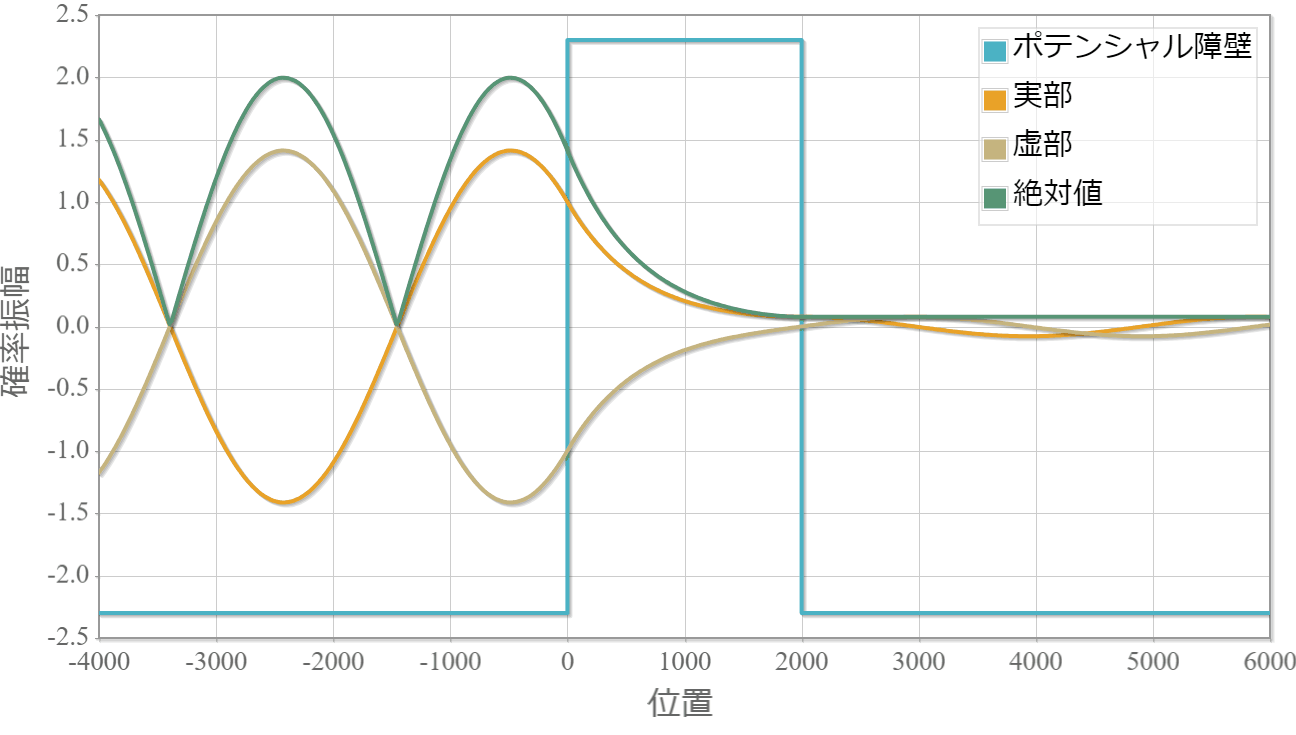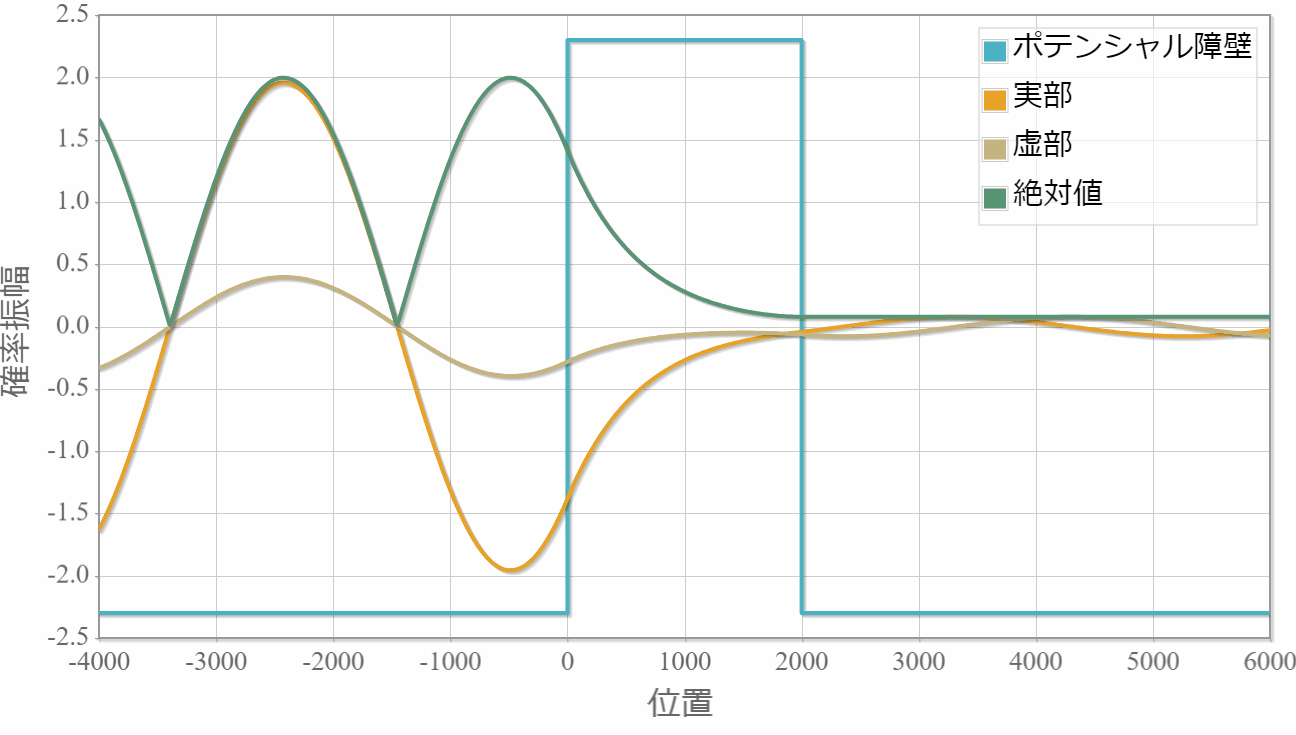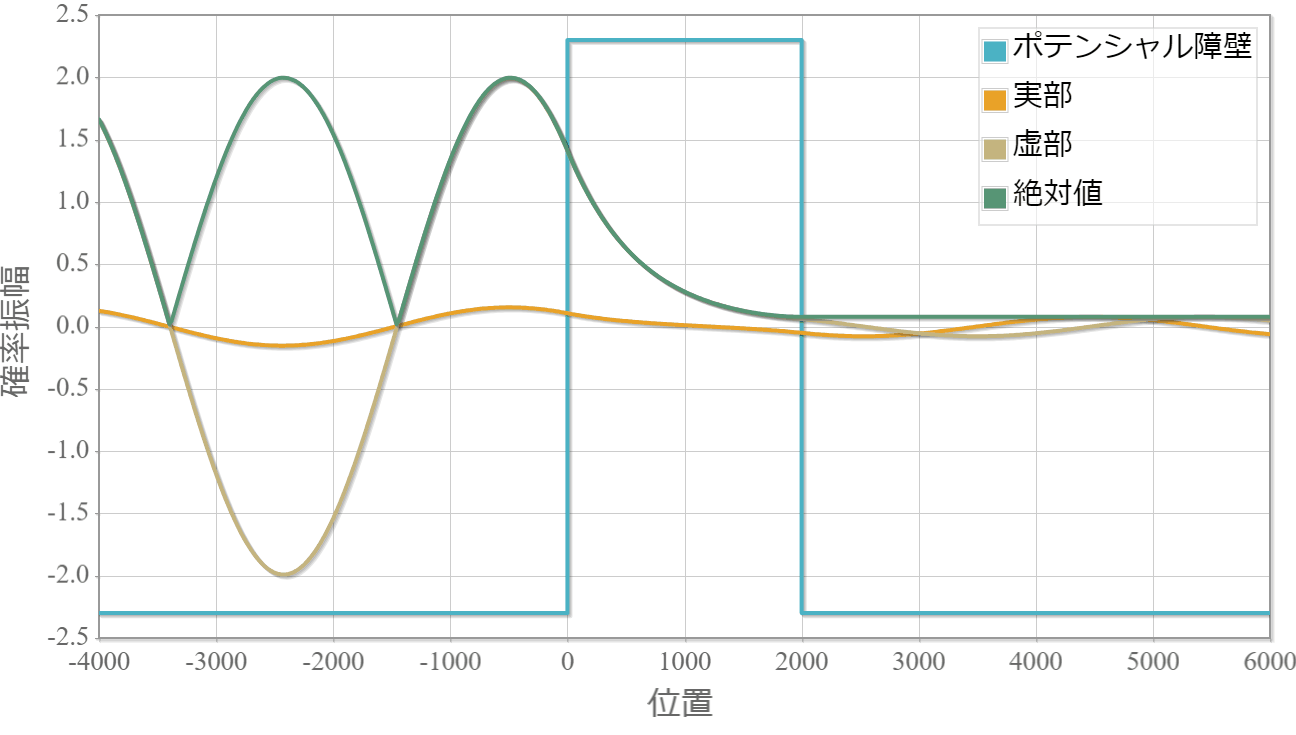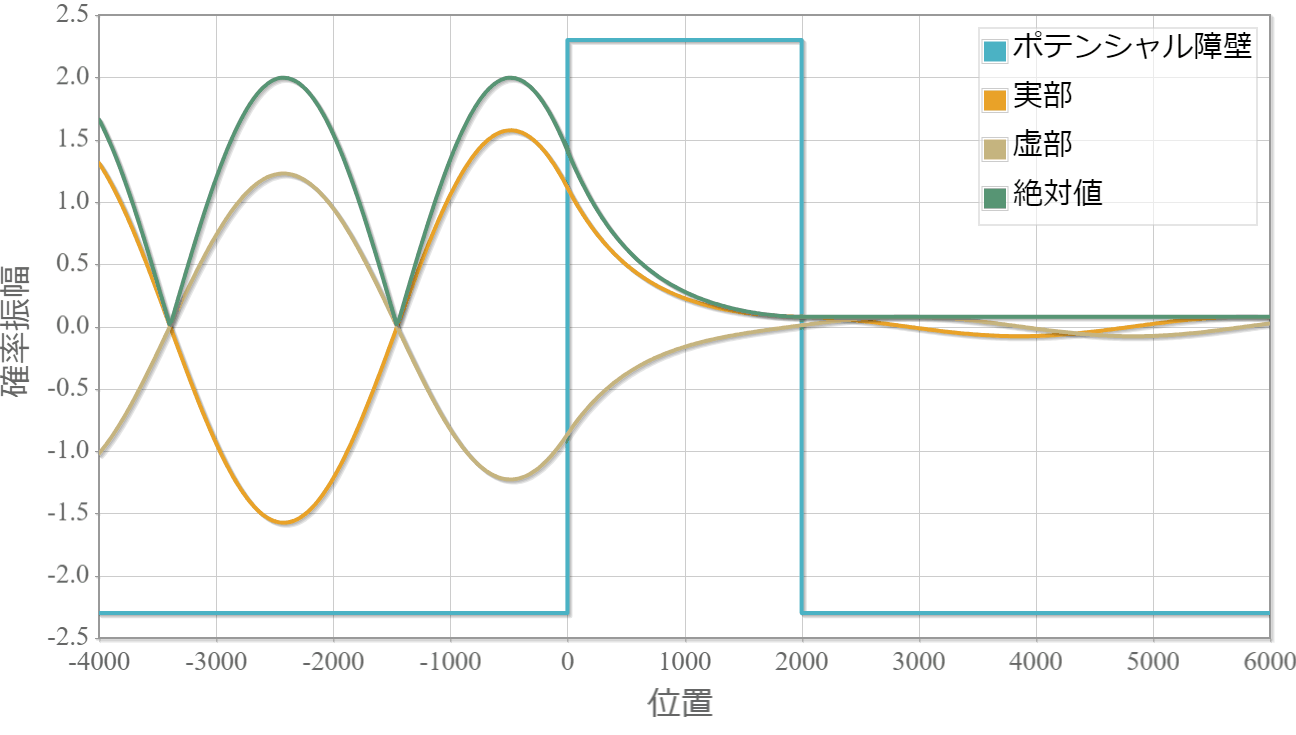
箱型ポテンシャル障壁でトンネル効果が生じている単一平面波の様子です。左より入射してます。
計算パラメータ
ポテンシャルの高さ: V2 = 20.0 * eV
平面波のエネルギー:E0 = 10.0 * eV;
空間スケール 1E-13[m];//横軸の値
考察と次の課題
・境界面でもなめらかに接続する様子がわかります。
・絶対値が時間に依存しないのは定常解であるためです。
・次は波束を箱型ポテンシャル障壁へ衝突させます。
プログラムソース(C++)
・http://www.natural-science.or.jp/files/physics/QuantumPhysics7.cpp
※VisualC++、GCC(MinGW)で動作確認しています。

































