【量子力学再入門9】
シュレディンガー方程式の数値解法（スペクトル法）

文責：遠藤理平（2018年5月11日）カテゴリ：仮想物理実験室(325)｜計算物理学(165)

量子力学とは原子や電子といったナノスケールにおける粒子の運動を記述する物理学の一分野です。メートルスケールで成り立つ「ニュートンの運動方程式」に対して、量子力学では「シュレディンガー方程式」と呼ばれる基礎方程式が成り立つと考えられています。これまでは解析的に得られている固有関数の重ねあわせで波束の運動をシミュレーションしました。しかしながら、シュレディンガー方程式で固有関数が解析的に得られるのは非常に稀な系だけで、多くの系では数値的に計算する必要があります。そこで本稿ではスペクトル法と呼ばれるシュレディンガー方程式の数値解法を導入します。

スペクトル法による解法

シュレディンガー方程式は波動方程式なので解は一般の有限差分法による数値計算を行うことができます。本稿では有限差分法よりも高精度な計算が可能なスペクトル法というアルゴリズムを用います。スペクトル法というのは、求めたい波動関数を正規直交系で展開した展開係数の時間発展を計算するというアルゴリズムで、最も簡単なのはフーリエ級数展開を用いるものです。シュレディンガー方程式から展開係数の時間発展を表す常微分方程式を導きます。波動関数とポテンシャル項を

$\psi(x,t) =\sum\limits_{n} a_n(t) \, e^{ik_nx}$
$V(x,t) =\sum\limits_{l} v_l(t) \, e^{ik_lx}$

と波数空間で展開して、時間依存性はその係数部分に含めます（ $-L/2\leq x\leq L/2$ ）。これらを元のシュレディンガー方程式に代入します。

$i\hbar\sum\limits_{n} \frac{da_n(t)}{dt} \,e^{ik_nx} = \sum\limits_{n}\frac{\hbar^2k_n^2}{2m}\, a_n(t)e^{ik_nx} +\sum\limits_{n}\sum\limits_{l} v_l(t)a_n(t)\, e^{ik_nx}e^{ik_lx}$

この関係式からx依存性を排除するために、両辺に $\exp^{-ik_{n'}x}$ を掛けてxで積分を行います。直交関係から

$i\hbar\sum\limits_{n} \frac{da_n(t)}{dt}\, \delta_{nn'} = \sum\limits_{n}\frac{\hbar^2k_n^2}{2m}\, a_n(t)\delta_{nn'} +\sum\limits_{n}\sum\limits_{l} v_l(t)a_n(t)\, \, \delta_{n+l,n'}$

となるので、最終的に次の表式が導かれます。

$i\hbar\,\frac{da_n(t)}{dt} = \frac{\hbar^2k_n^2}{2m}\, a_n(t) +\sum\limits_{l} v_l(t)a_{n-l}(t)$

これはn=0～N-1までのN個の連立常微分方程式となっています。本稿ではこれをルンゲ・クッタ法を用いて解きます。

シミュレーション結果

中心エネルギーE0 = 0 の波束の時間発展と解析解との差である計算誤差を示します。

波動関数の空間分布

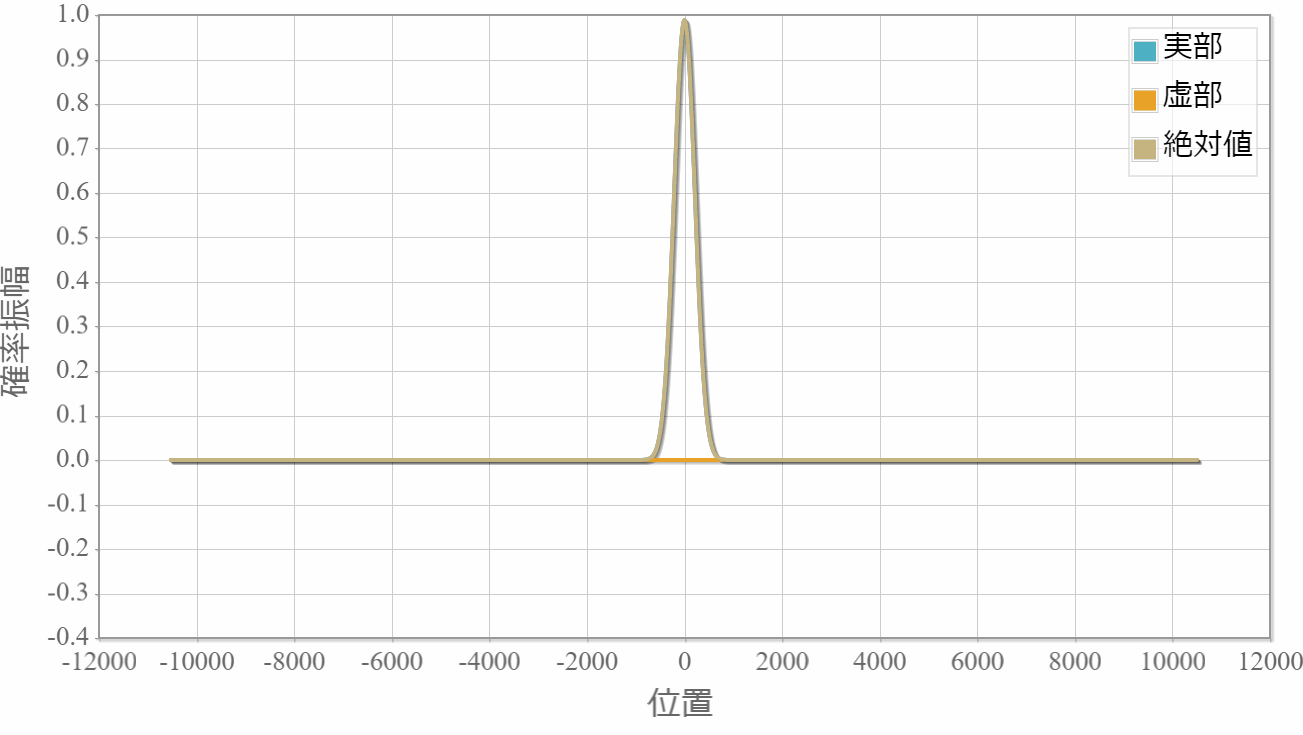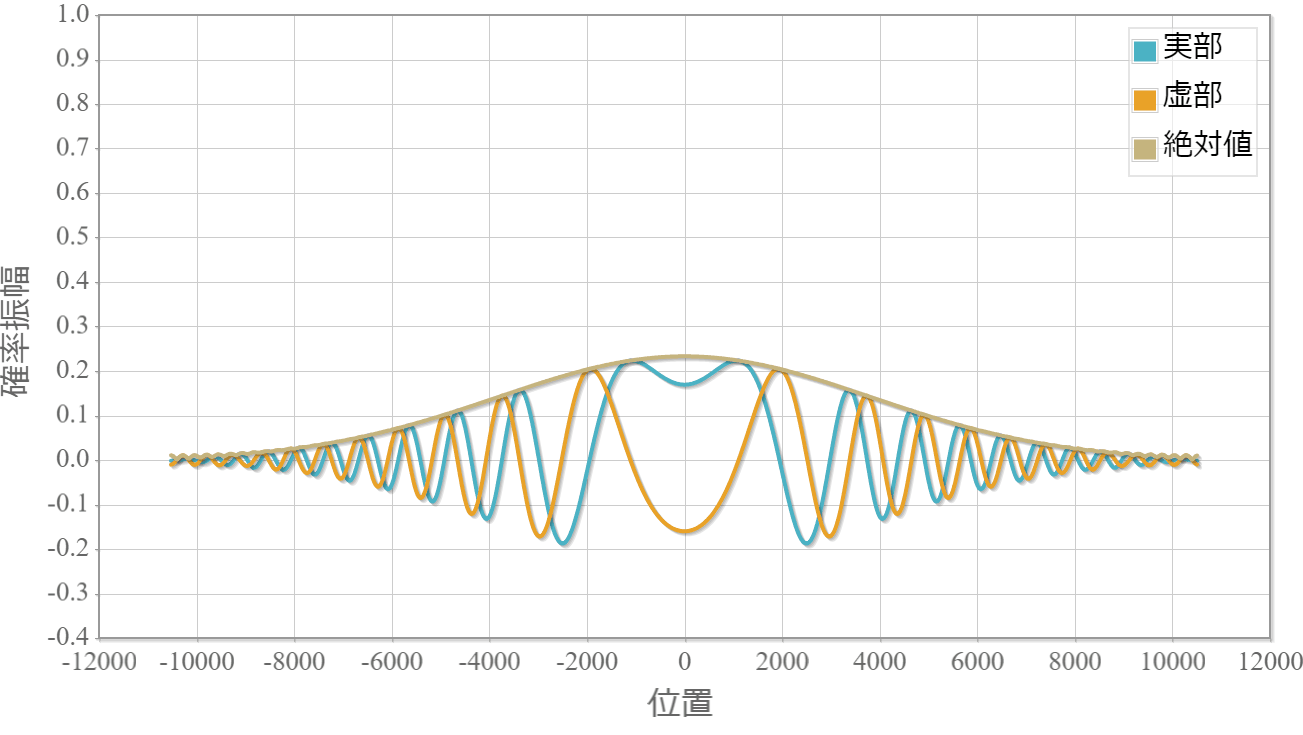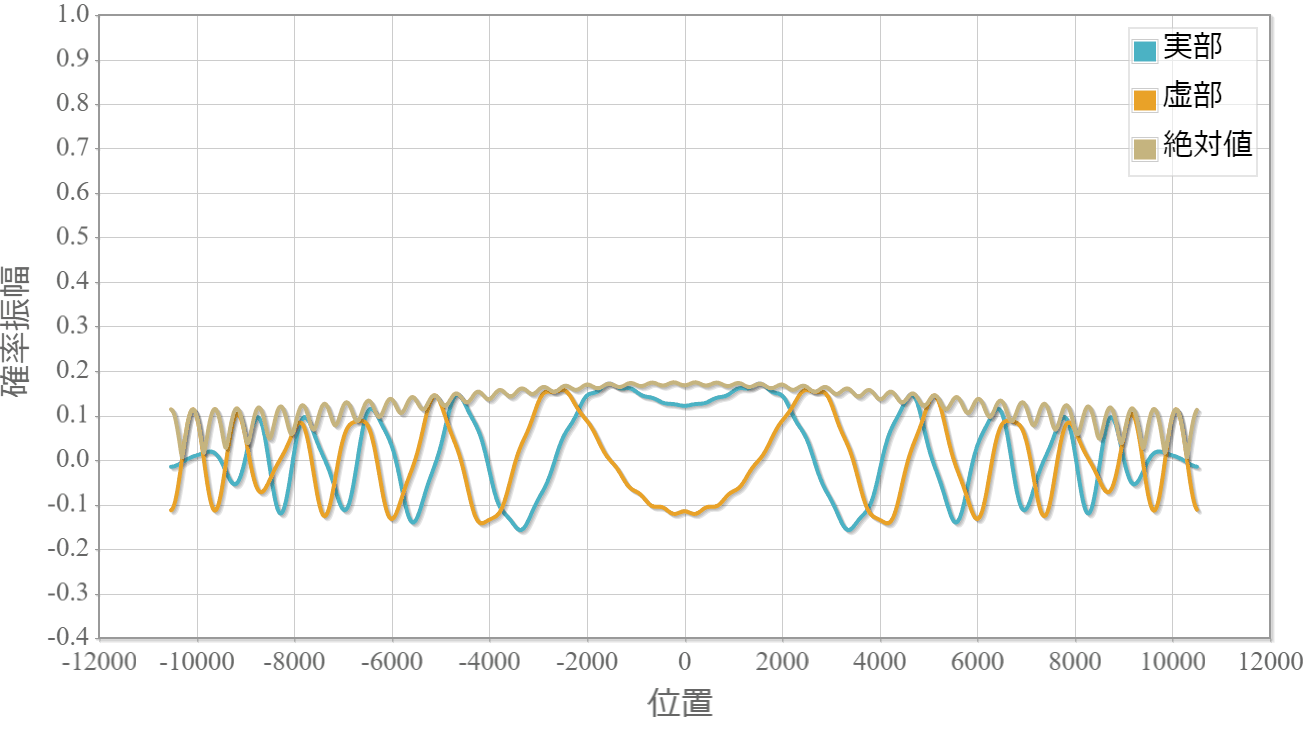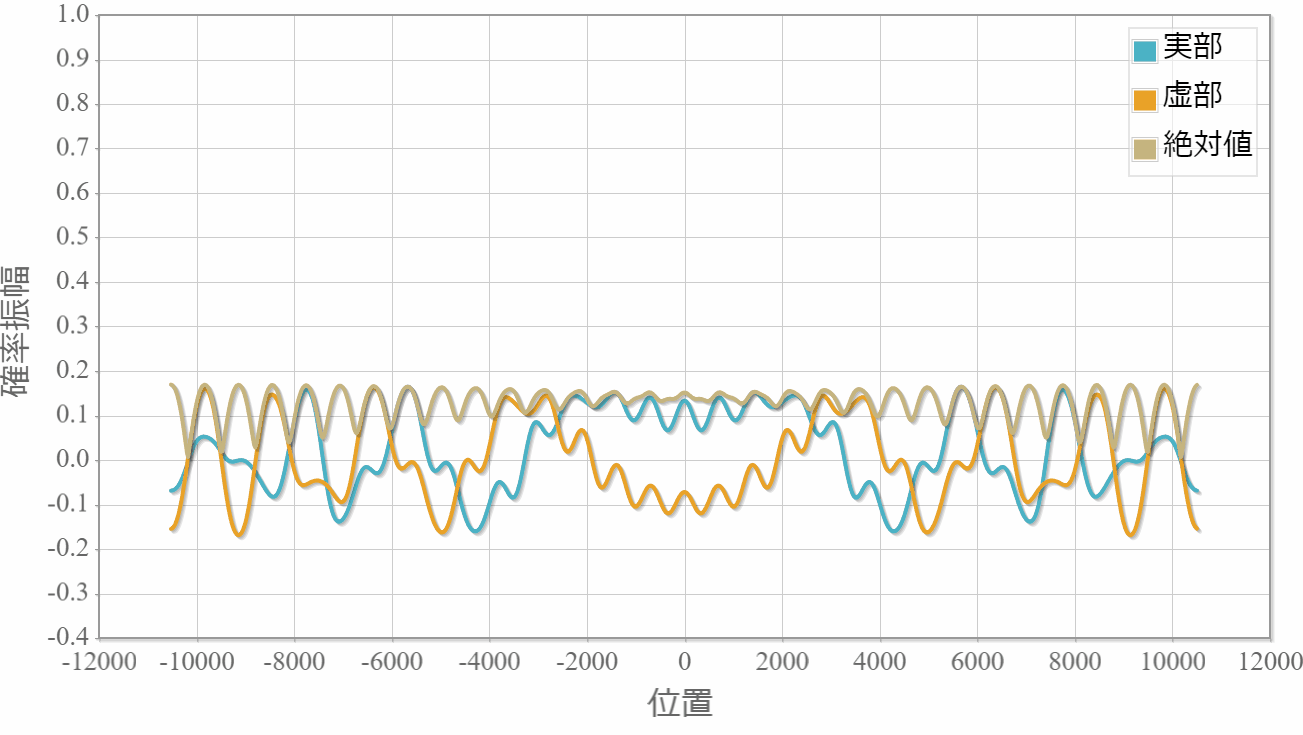
計算誤差

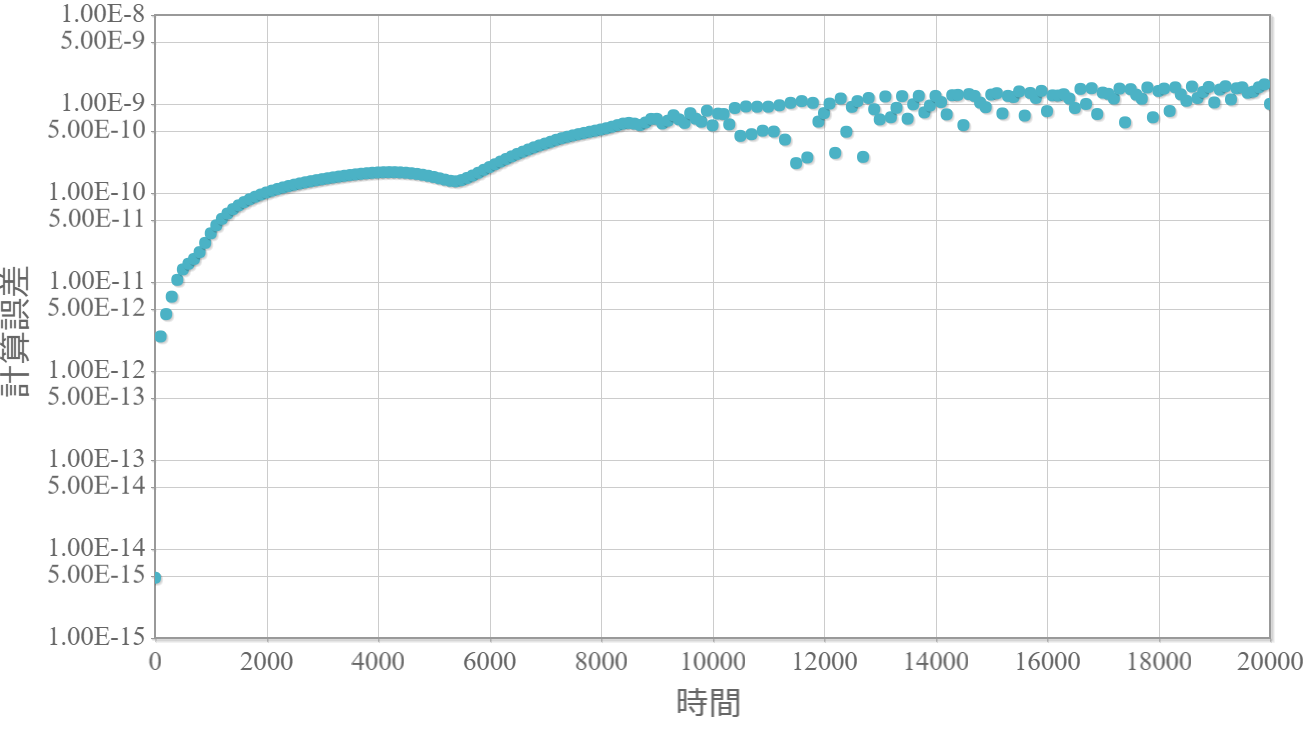
計算パラメータ

空間スケール 1E-11[m];//横軸の値
時間スケール 1E-14[s];//１コマの時間
数値計算の時間間隔1E-16[s]

考察と次の課題

・ポテンシャルが存在しない系で動作は確認できた。
・次は箱型ポテンシャル障壁に波束を衝突させる系で誤差チェックを行う。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics_OpenMP.zip
※VisualC++、GCC（MinGW）で動作確認しています。

	【受講生募集】『natural science 科学・技術講座』新講座のご案内 2024.01.09 【大草芳江｜TOPICS】
	サイエンス・デイオブザイヤー2023贈賞式（文部科学大臣賞表彰等）を開催しました 2023.11.07 【大草芳江｜TOPICS】
	■「natural science 科学・技術講座」夏休み短期講座のご案内 2023.07.14 【遠藤理平｜TOPICS】
	「国際イノベーションコンテスト2022世界大会」でnatural science『科学・技術講座』チームが世界3等入賞 2023.07.12 【大草芳江｜TOPICS｜パブリシティ】
	サイエンス・デイ限定『学都「仙台・宮城」サイエンスマップ～光編～』第7版プレゼント申込開始（先着500名）！ 2023.07.08 【遠藤理平｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2023　7月16日（日）開催！ 2023.07.08 【大草芳江｜TOPICS】
	人材募集のご案内 2022.08.19 【大草芳江｜TOPICS】
	学都「仙台・宮城」サイエンス・デイ2022　7月17日（日）開催！ 2022.07.01 【大草芳江｜TOPICS】
	「第13回国際イノベーションコンテスト2022」国内予選大会　natural science チームが第３位入賞、４年連続通算８回目の世界大会出場へ 2022.05.23 【大草芳江｜TOPICS】
	「キャンパスベンチャーグランプリ2021」東北大会で最優秀賞、全国大会で日刊工業新聞社賞を受賞 2022.03.09 【大草芳江｜TOPICS】
	【プレスリリース】「第12回国際イノベーションコンテスト2021」世界大会　natural science チームが世界３等入賞 2022.01.17 【大草芳江｜TOPICS】
	【第８話】有限の高さの障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.29 【遠藤理平｜仮想物理実験室】
	【第７話】無限に高い障壁に向けた電子パルスの照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.24 【遠藤理平｜仮想物理実験室】
	【第６話】無限に高い障壁へ照射アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.23 【遠藤理平｜仮想物理実験室】
	【第５話】電子パルスの運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.21 【遠藤理平｜仮想物理実験室】
	【第４話】電子パルスの作り方【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.20 【遠藤理平｜仮想物理実験室】
	【第３話】自由粒子の運動アニメーション【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.19 【遠藤理平｜仮想物理実験室】
	【第２話】自由粒子のスナップショット【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.18 【遠藤理平｜仮想物理実験室】
	【第１話】プログラムの動作確認【Pythonコピペで量子力学完全攻略マニュアル】 2021.09.17 【遠藤理平｜仮想物理実験室】
	「natural science 科学・技術講座」講師３人で設立した株式会社weCAN。アイディアの商品化第一弾「美姿勢メガネ」を朝日新聞さんに取材いただきました。 2021.08.23 【遠藤理平｜パブリシティ】

【量子力学再入門9】
シュレディンガー方程式の数値解法（スペクトル法）

スペクトル法による解法