【機械学習基礎研究2】
倒立状態維持の強化学習（貪欲性による学習成果の違いについて）
本稿では、強化学習の中でも最も基本的なQ学習を用いて【ルンゲ・クッタで行こう！】水平自由単振子運動シミュレーションで準備した水平方向には自由に動く支点と伸び縮みしない質量のないひも（棒）で結ばれたおもりを用いて、強化学習の基本中の基本である倒立振子の倒立状態を維持するための行動をQ学習で学習させてみます。Q学習も沢山のパラメータが存在しますが、全く初めてなのでどのような値を与えればよいか検討がつかないため、これから当面はパラメータによる学習成果を違いを確かめてみます。
水平自由単振子の数理モデル
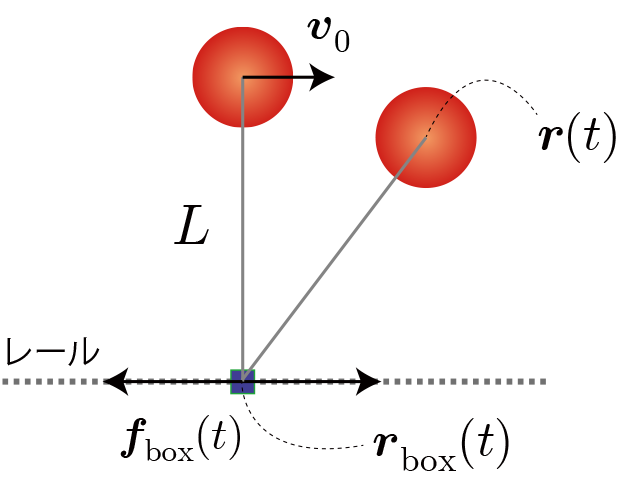
水平方向（x軸方向）に自由に動くことのできる支点を本稿では滑車と呼びます。滑車とおもり質量と位置ベクトルを$m_{\rm box} $, $m$、$\boldsymbol{r}_{\rm box} (t)$, $ \boldsymbol{r}(t)$、伸び縮しないひもの長さを$L$、滑車に与える外力を$ \boldsymbol{f}_{\rm box} $と表しています。初期状態はおもりを滑車の真上に配置して、初速度 $ \boldsymbol{v}_0$（-1.0～1.0[m/s]）を与えるとします。状況に応じて滑車に外部から力を与えることで倒立状態を維持させることを目標とします。数値計算は最大５秒間とし、おもりが滑車よりも下に行った時点で終了として、改めて初期状態からスタートすることにします。
Q学習のパラメータ
環境と行動と利得の定義（行動価値関数の定義）
Q学習における環境は要素を増やすごとに指数関数的に場合の数が増加します。そこで、今回は環境として最も重要な要素はと考えられる滑車とおもりの相対位置のみを考慮します。 今回は相対位置（x座標）を10個に分割して（環境の場合の数＝１０）、それぞれの「環境」に対して滑車へ「行動」として力を与えます。なお、力の分割数は２０個とします。以上より、環境：１０、行動：２０となり、最適行動価値関数は１０×２０の配列で表せます。
なお、利得はおもりの位置エネルギー（$mgz$）とし、目標達成（５秒間落下しない）やペナルティー（５秒以内に落下）は今回与えないことにします。
Q学習の表式とパラメータの値
\begin{align} Q^{(i+1)}(s,a) \leftarrow Q^{(i)}(s,a)+\eta\left[ r+\gamma \max\limits_{a'} Q^{(i)}(s',a') -Q^{(i)}(s,a) \right] \end{align}
$s$ ： 時刻tにおける状態。$s(t)$と同値。
$a$ ： 時刻tにおける行動。$a(t)$と同値。
$r$ ： 時刻tの行動で得られた利得。$r(t+1)$と同値。
$Q(s, a)$ ： 状態$s$における行動aに対する行動価値関数。上付き添字（$i$）は学習回数を表す。
$\gamma$ ： 割引率（$0< \gamma \le 1$）
$\eta$ ： 学習率（$0< \eta \le 1$）
$s'=s(t+1)$
今回の設定
行動時間間隔：0.01（0.01秒ごとに行動を選択・実行する）
学習回数（episode）：3000
学習率（$\eta$）：0.1（行動価値関数の更新時の変化率）
割引率（$\gamma$）：0.5（未来に得られると期待される報酬を割り引くかを表す率）
今回は行動価値関数で予測される利得の期待値が最大となる行動を選択する率（貪欲率$\epsilon$）を0～1.0まで変化させて、その結果を比較します。
学習結果
貪欲率$\epsilon$を0から1.0まで0.1ずつ変化させた際の、学習回数に対する倒立振子が落下するまでの時間（落下時間）をグラフ化した結果を示します。 落下時間が５秒は落下しなかったことを意味します。
$\epsilon=0$（行動はランダムの場合）
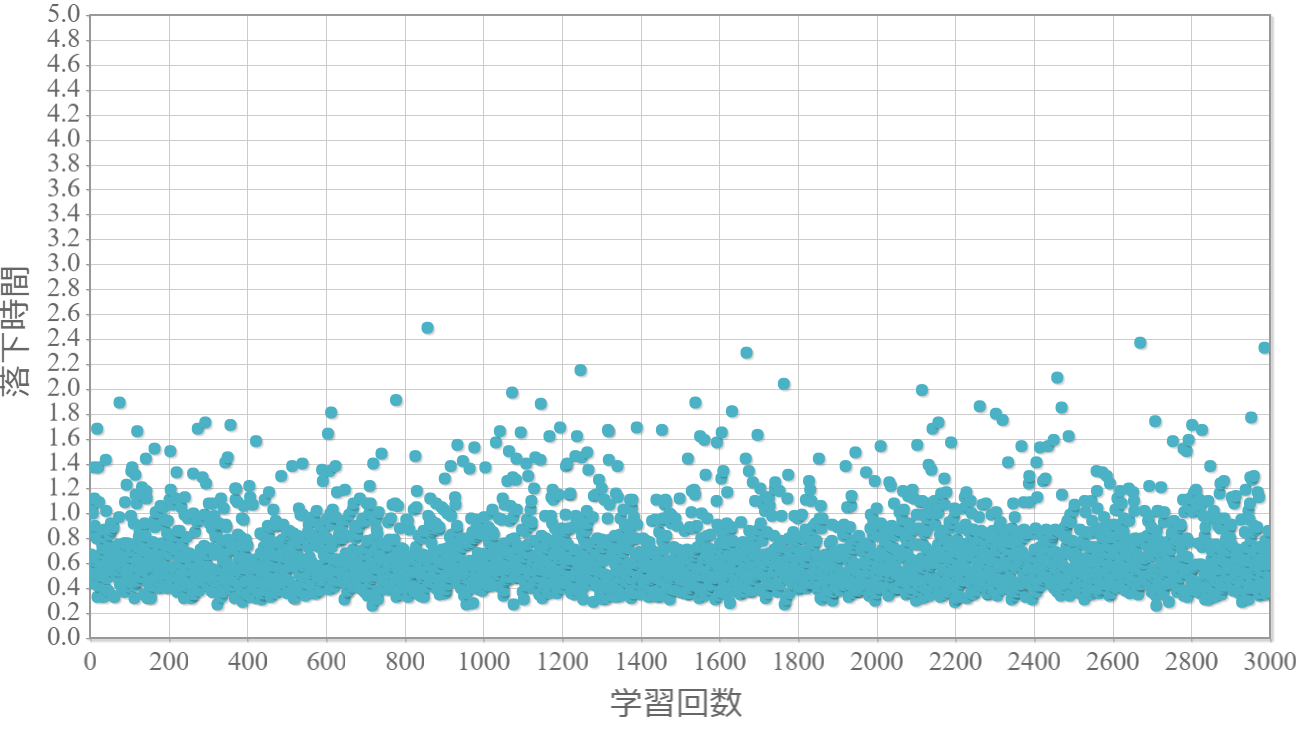
$\epsilon=0.1$
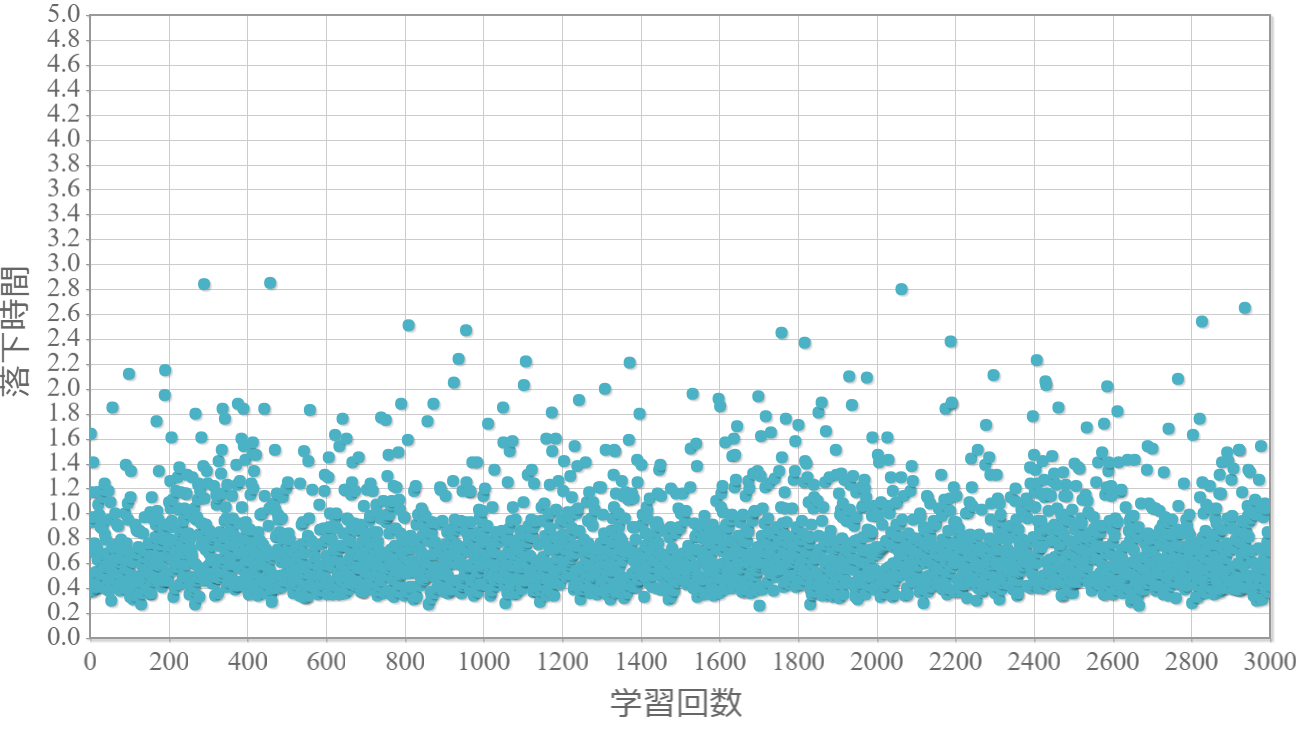
$\epsilon=0.2$
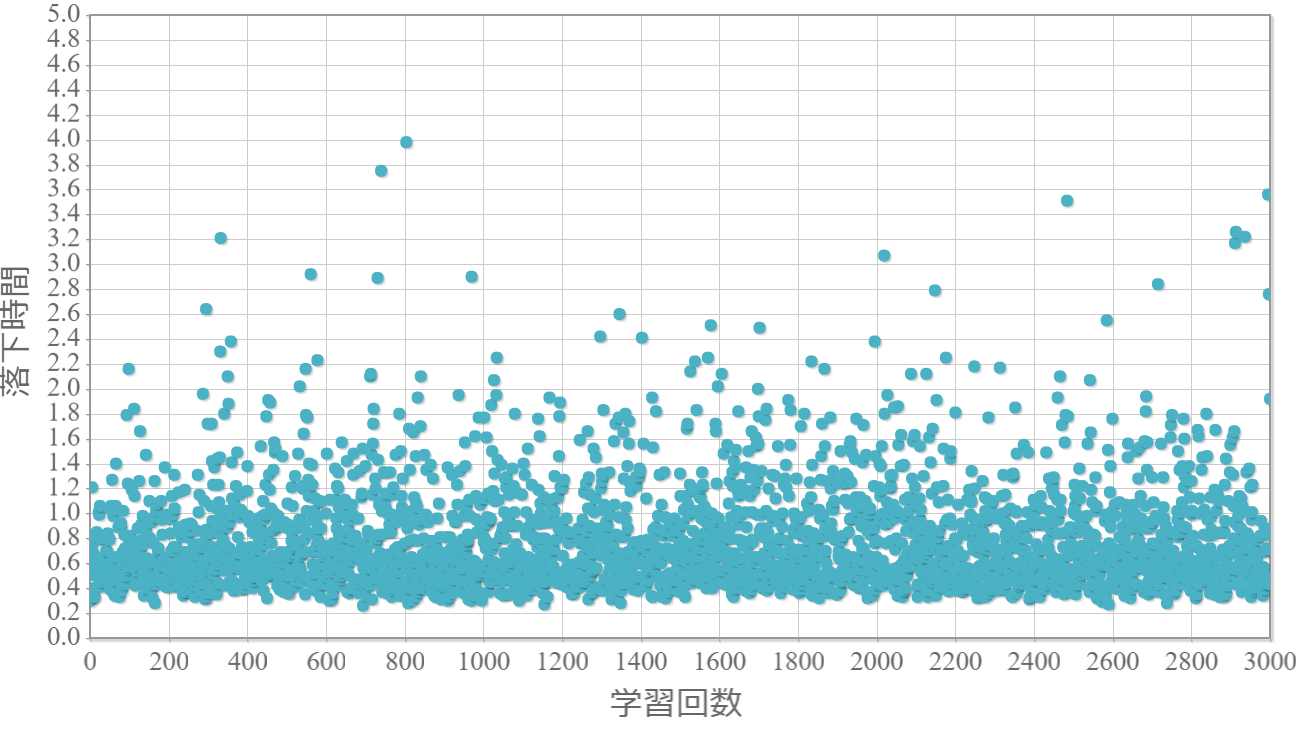
$\epsilon=0.3$
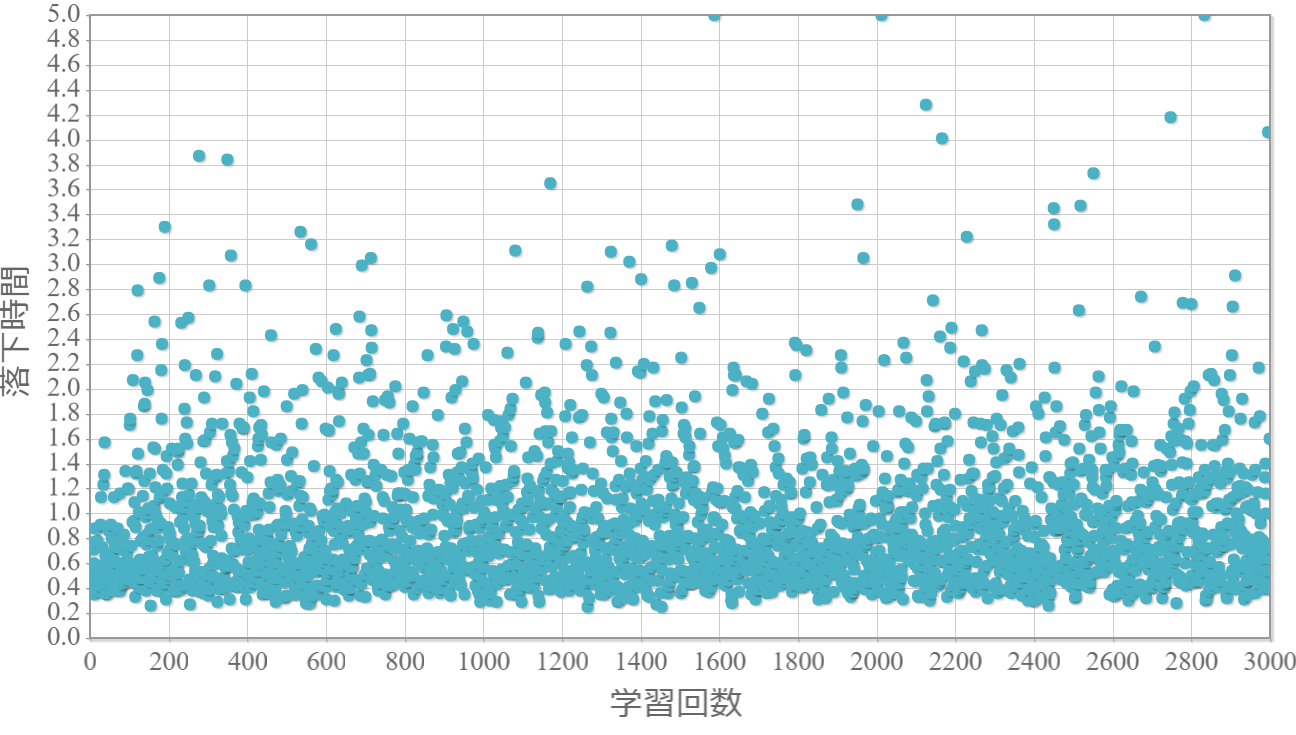
$\epsilon=0.4$
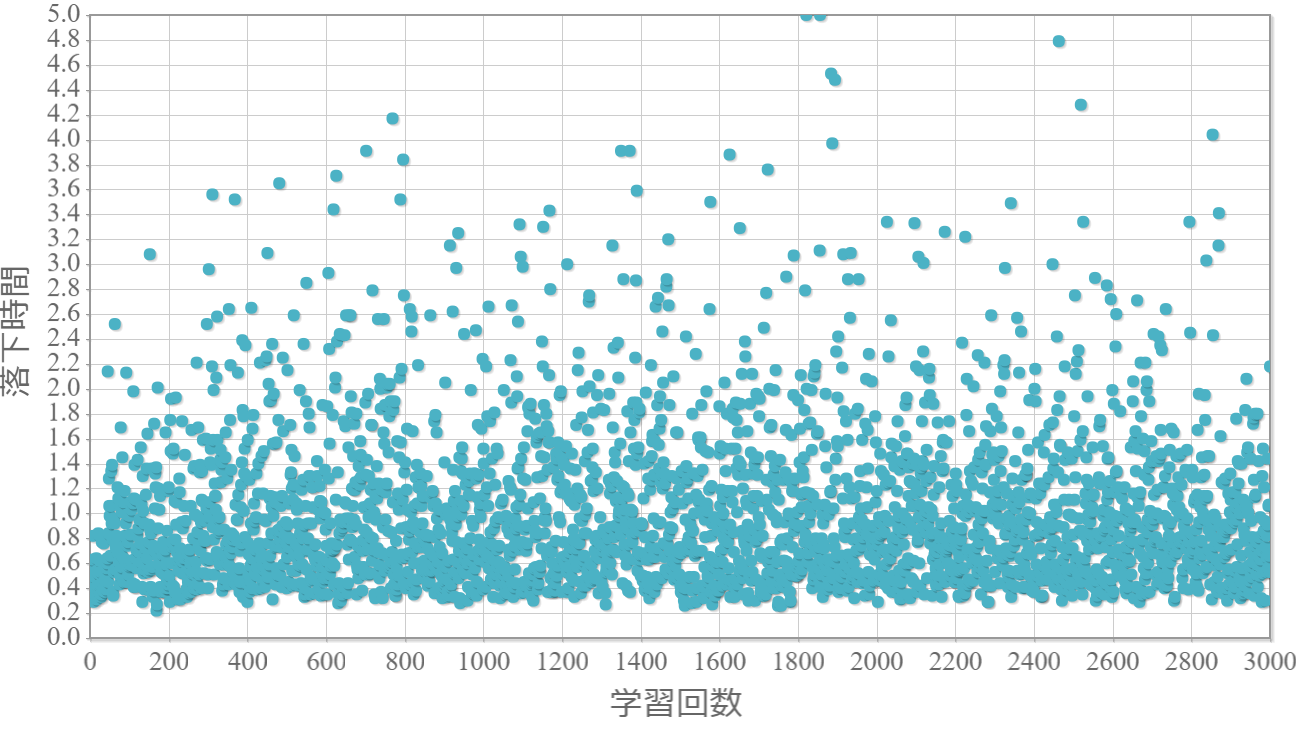
$\epsilon=0.5$
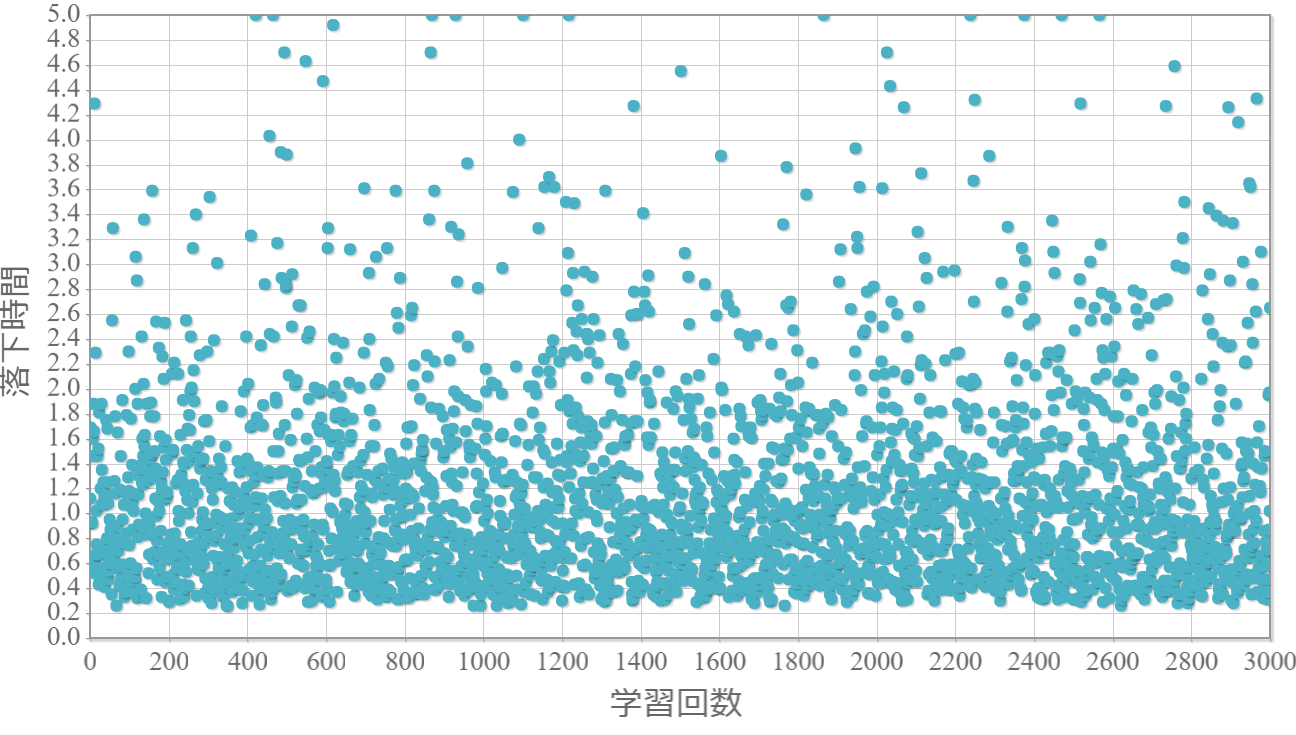
$\epsilon=0.6$
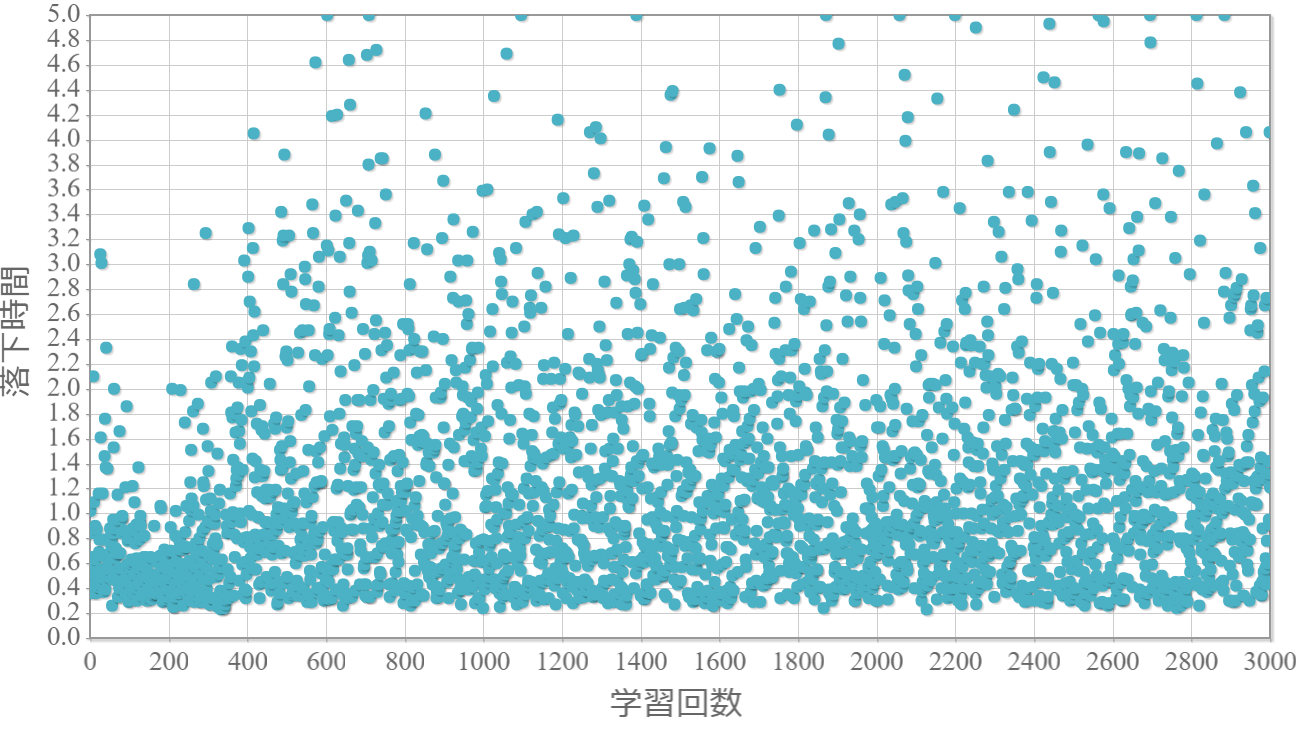
$\epsilon=0.7$
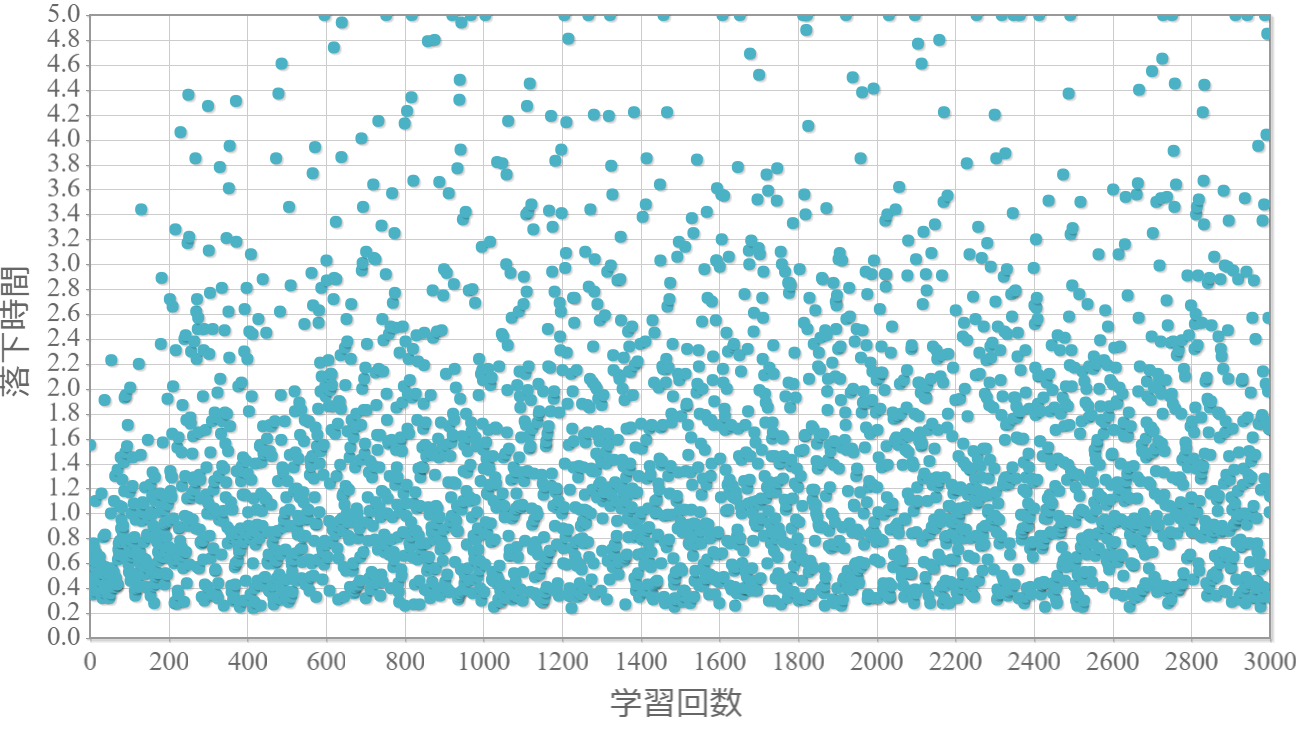
$\epsilon=0.8$
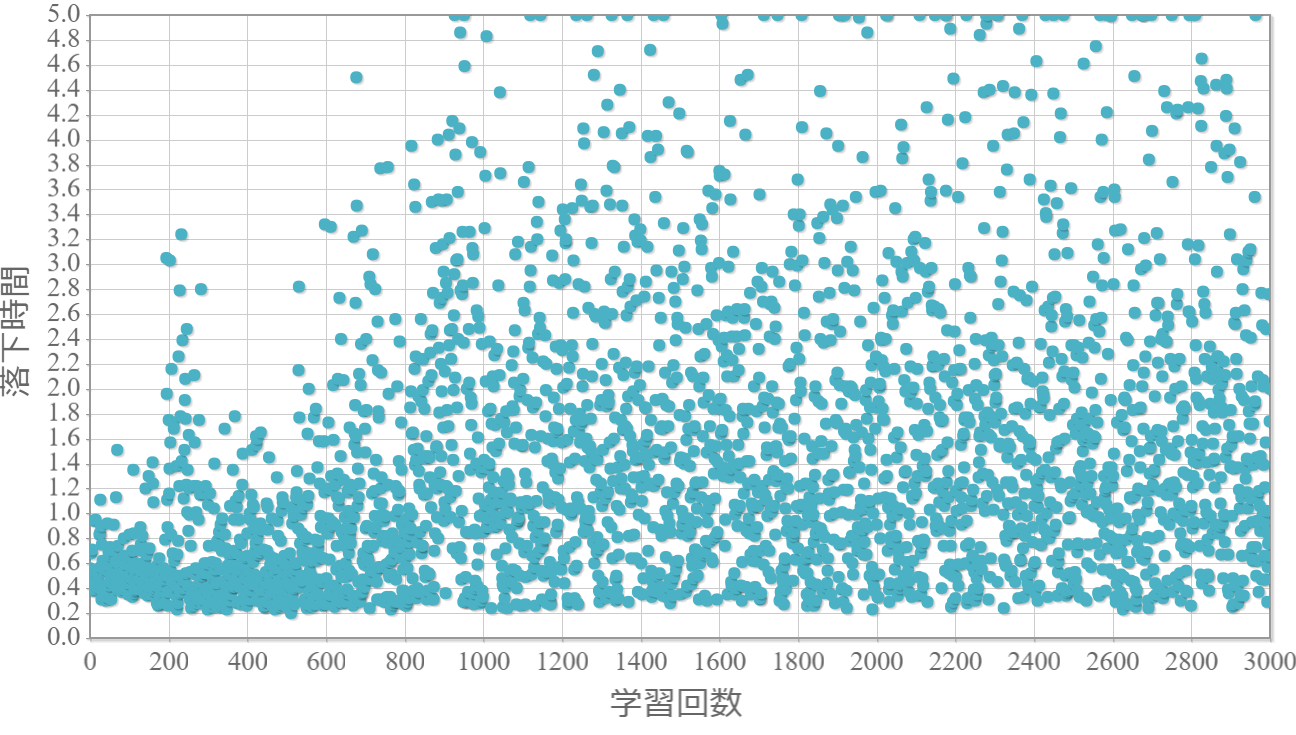
$\epsilon=0.9$
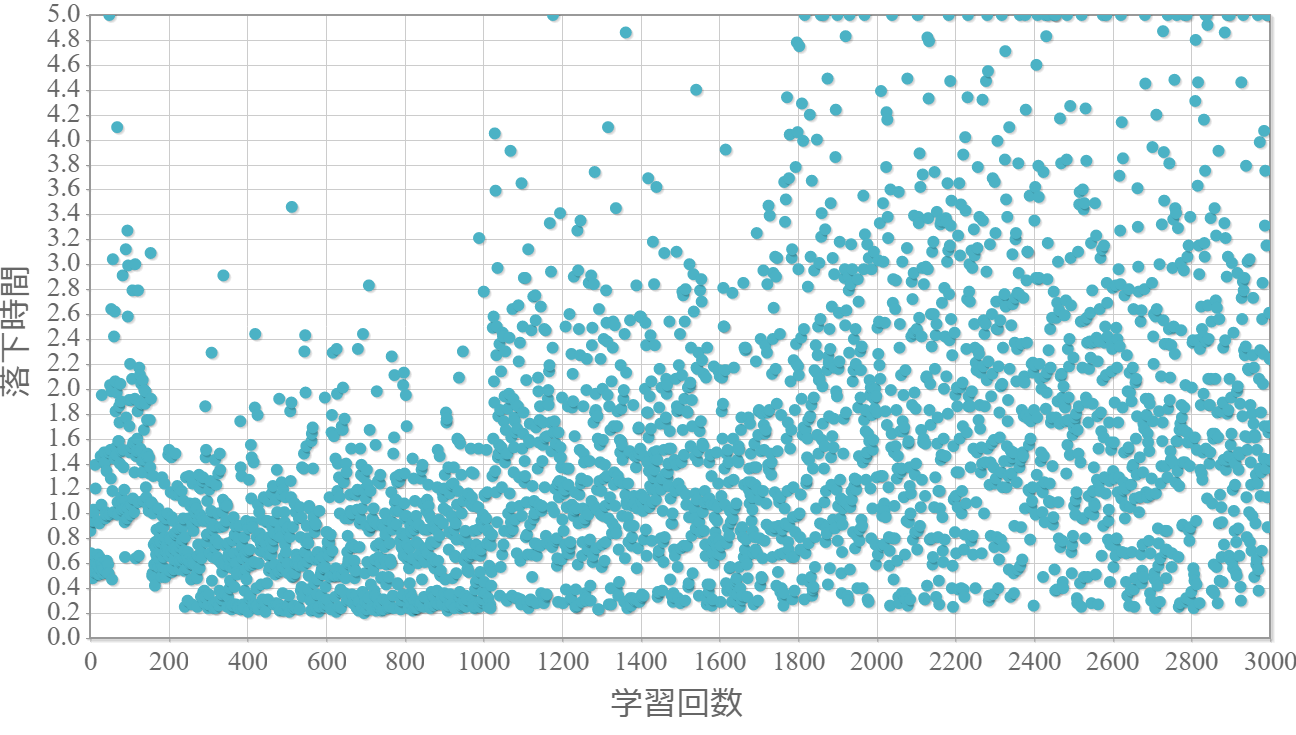
$\epsilon=1.0$
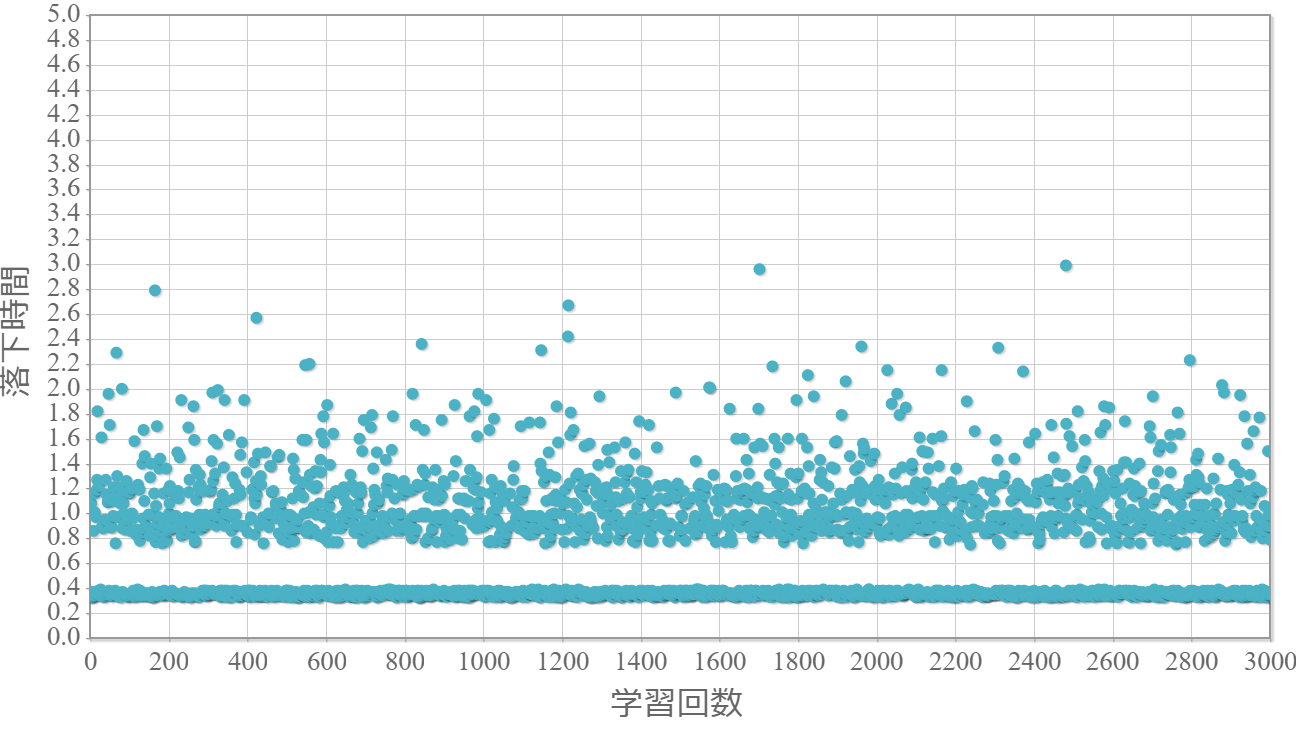
結果と考察とメモ
・貪欲率が0.3あたりから目標達成（落下時間5秒）がみられ、0.7あたりまでは達成する回数が増えていく。
・貪欲率0.5 → 0.6 →0.7 → 0.8 → 0.9 にかけて目標達成が後ろ（学習回数が多い方）に偏る傾向が強くなる。
→ 貪欲率が高いほど、学習序盤の中途半端な利得に対する影響が大きくなる
→ 貪欲率が高いほど、学習が進んだ後の目標達成確率は高い（ように見える）。
・貪欲率が1.0の場合には目先の利得だけで行動するため、最終的な目標達成はできない。
【メモ】割引率を変える
【メモ】学習率を変える
【メモ】貪欲率を学習状況によって変化させる
プログラムソース（C++）
・20180606-1.zip
※VisualStudio2017のソルーションファイルです。GCC（MinGW）でも動作確認しています。
参考（物理シミュレーション）
上記シミュレーションは、ルンゲ・クッタ法という常微分方程式を解くアルゴリズムを用いてニュートンの運動方程式を数値的に解いています。本稿で紹介した物理シミュレーションの方法を詳しく解説している書籍です。もしよろしければ「ルンゲ・クッタで行こう！～物理シミュレーションを基礎から学ぶ～（目次）」を参照ください。
