N重振り子のアルゴリズムとシミュレータ
これまで,以下の振子の運動シミュレーションを行ってきました.
・ラグランジュ運動方程式1:極座標を用いた単振子
・ラグランジュ運動方程式2:極座標を用いた球面振子
・ラグランジュ未定乗数法を用いた球面振子のシミュレーション
・ラグランジュ未定乗数法を用いた2重振子のシミュレーション
これまでのシミュレーションを見てきて,おもりの数が増えたらどんな動きをするのだろうか?
という疑問が湧いた人もいると思います.
ここでは,N重振り子の運動方程式を定式化し,HTML5(canvas要素)+WebGL(Three.jsライブラリ)を用いた,
プラグインなしでお手軽に実行できるシミュレータで,その運動を再現します.
3次元空間中にある,質量のない剛体棒でつながれたN個の質点で構成された振り子の運動方程式を求めてみよう!
ここでは,シミュレーションを行うことを前提として,N重振り子の運動方程式を記述していく.
また,一般的に振り子の運動を記述するときは,剛体棒の角度などを使うが,
この方法は座標の数が減り解析がしやすくなる反面,
質点が剛体棒から受ける拘束力などといった情報がカットされているのだ.
したがって今回は,質点のデカルト座標系における位置と質点が剛体棒から受ける拘束力
で振り子の運動を記述してみようと思う.
運動方程式を求める前に,振り子を構成する要素に名前を付ける.
振り子が固定されている点を,
固定点から数えて
番目の質点の位置を
,
その質点の質量を
とする.
また,振り子の質点の数をN,重力加速度を
とする.
番目の質点には,重力
と,
前の質点との間に働く張力
,
後の質点との間に働く張力
が作用する.
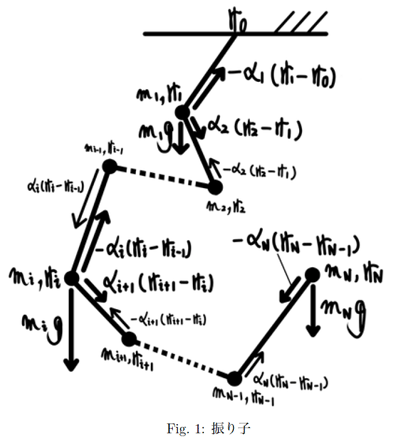
運動方程式と,その解き方の方針
これを運動方程式に書き表すと式(1)のとおりとなる.
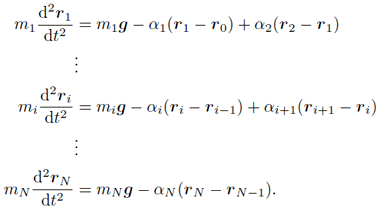
上式における,位置,速度
,張力に含まれる係数
という
7N個の変数を求めれば,振り子を再現できるのだ!!
さて,求めたい変数は7N個あるのだが,式(1)は3N本しかない.
どうするのか?
まず,「一階化」というテクニックや「拘束条件」を使って式の本数を7N本とし,未知変数と式の数を一致させる.
この操作をすると,位置,速度
をRunge-Kutta法などの差分スキームを使って求めることができる.
ただ,
が決まらなければ,位置
,速度
は決めることができないのだ.
ということで,
をいかに決定するかということが,ここでのヤマ場となる.
結論からいうと,
に関する連立方程式を立式するのだが,
いろいろなベクトル演算のテクニックを存分に活用していくので,頑張ってついてきてくれ!!
一階化
まずは「一階化」を行う.
式(1)中にある加速度は求めたい変数ではないので,これを消去したい.
ということで式(1)を,
と
の一階微分だけで表現する.
これが「一階化」なのだ!
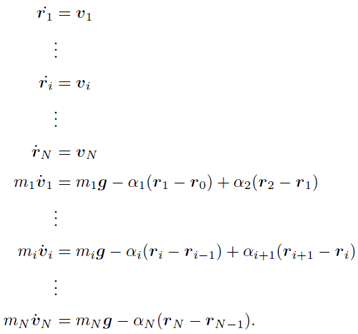
境界条件
しかし,一階化しても式(2)は6N本しかないので,まだ全ての変数を決定することはできない. そこで拘束条件を考えてみる. 各質点のあいだには質点間の距離を一定に保つ拘束条件がある. この条件式は式(3)となる.
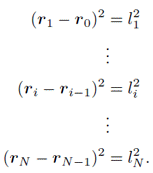
張力に含まれる係数 を求める
を求める
さて,これが今回のヤマ場だ!!
運動方程式(1)と拘束条件式(3)から,
位置と速度
で表現された,
張力に含まれる係数
に関する連立方程式を立式する.
この
さえ求められれば式(2)をRunge-Kutta法などの差分スキームで存分にブン回せるのだ!
まずは下ごしらえとして,式(3)を時刻で微分する
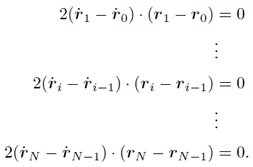
式(4)の両辺を2で割り,さらにもう1回で微分する.
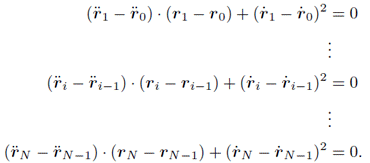
相対位置の二階微分
が出てきた!
運動方程式(1)からも,うまく
を出して消去すれば,
を求められそうだぞ!
ということで,式(1)の両辺を質量
で割ってみる.
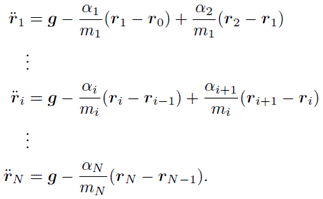
さてここでを出すために,
番目の式から
番目の式を辺々引く.
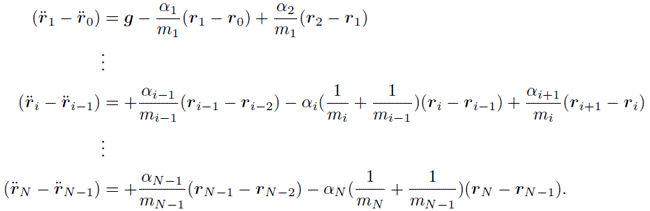
ここではどうするんだ?と思った人がいるかもしれない.
は固定点なので力がつり合っており
になっている,としておこう.
ここで式(7)の両辺と
の内積をとる.
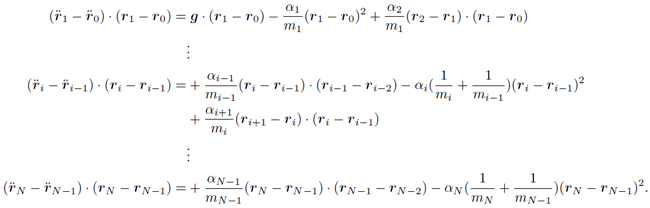
式(5)から導かれる関係式を使って,
式(8)の左辺にある相対位置の二階微分
を消そう.
これでやっと加速度を消去できたな!}
ついでに,後々のために右辺と左辺を入れ替えたり係数を掛ける順番を少し入れ替えておく.
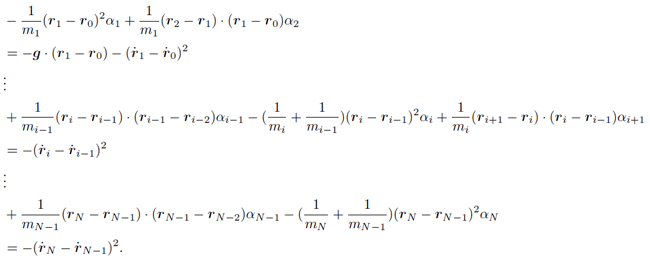
さて,これはについての連立方程式になりそうだな...
とりあえず式(9)を行列化してみよう.
式(9)を下記のとおりに置き換える.
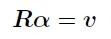
ただしここで,
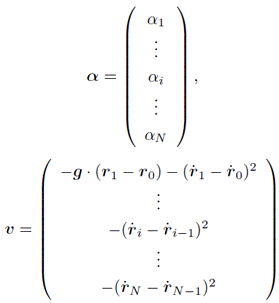
なのだが,は

となる.
あとは,Gauss-Jordanの消去法などを用いてを求めれば完了だ!
やっと
を求められたな!!おつかれっす!!
N重振り子シミュレータ
本シミュレータは、HTML5(canvas要素)+WebGL(Three.jsライブラリ)を用いて、プラグインなし実行することができます。 ただし、クライアントサイドのブラウザとグラフィックカードが、HTML5とWebGLに対応している必要があります。
↓デモ画像(「点電荷による電気力線シミュレータ」はこちら


































