【量子力学再入門10】
シュレディンガー方程式の数値解法（スペクトル法）の注意点

前回、シュレディンガー方程式を数値的に計算するスペクトル法というアルゴリズムを紹介しました。 この手法を実践で利用する前に、解析解が得られている系で数値解と比較することで、適切なパラメータの与え方を調べます。 今回対象とする系は波束の運動です。次のGIFアニメーションは中心エネルギーE0=10eVの波束の運動を、スペクトル法を用いて計算した結果です。 想定通りの計算が行えています。

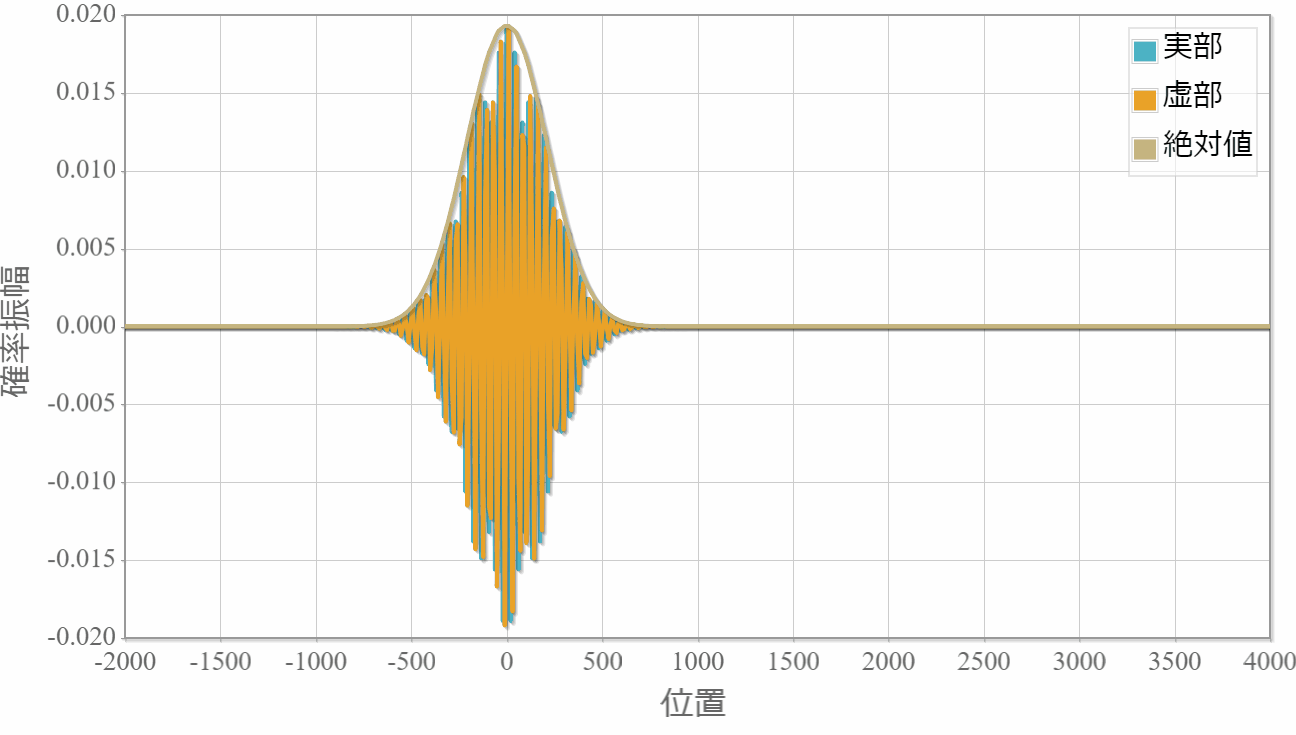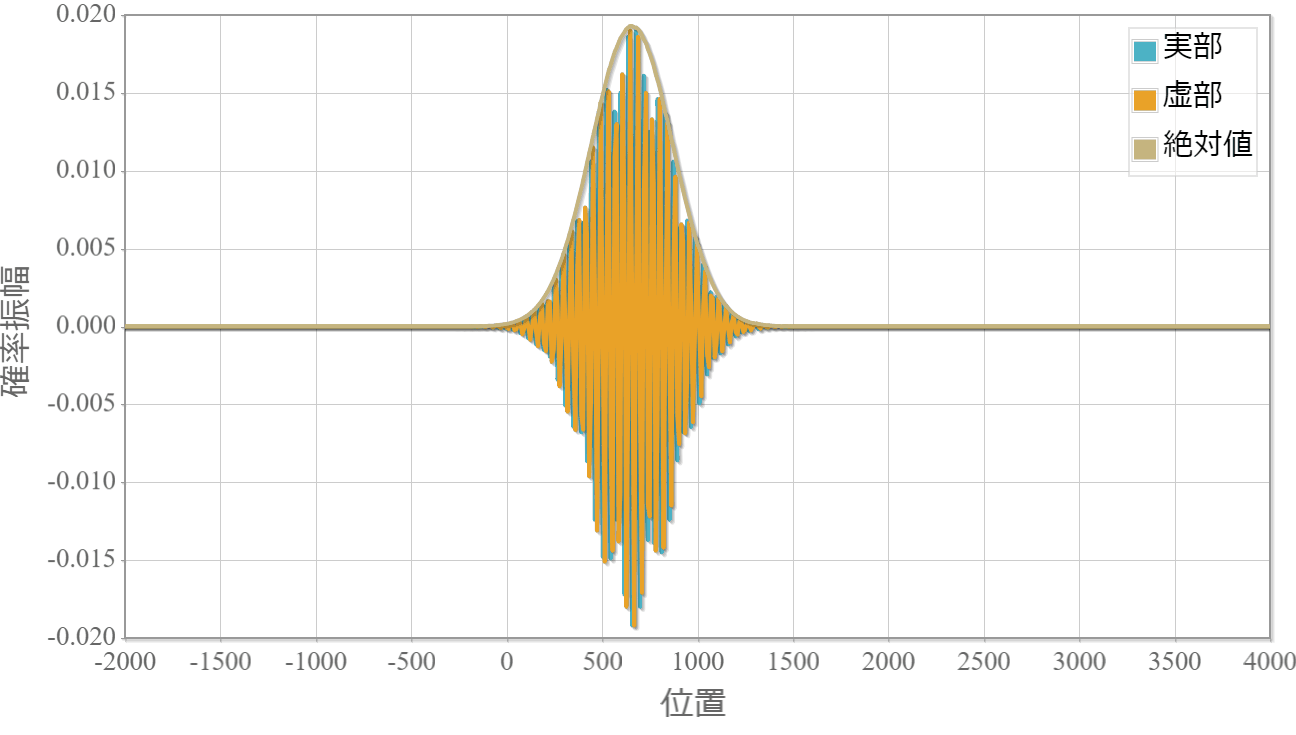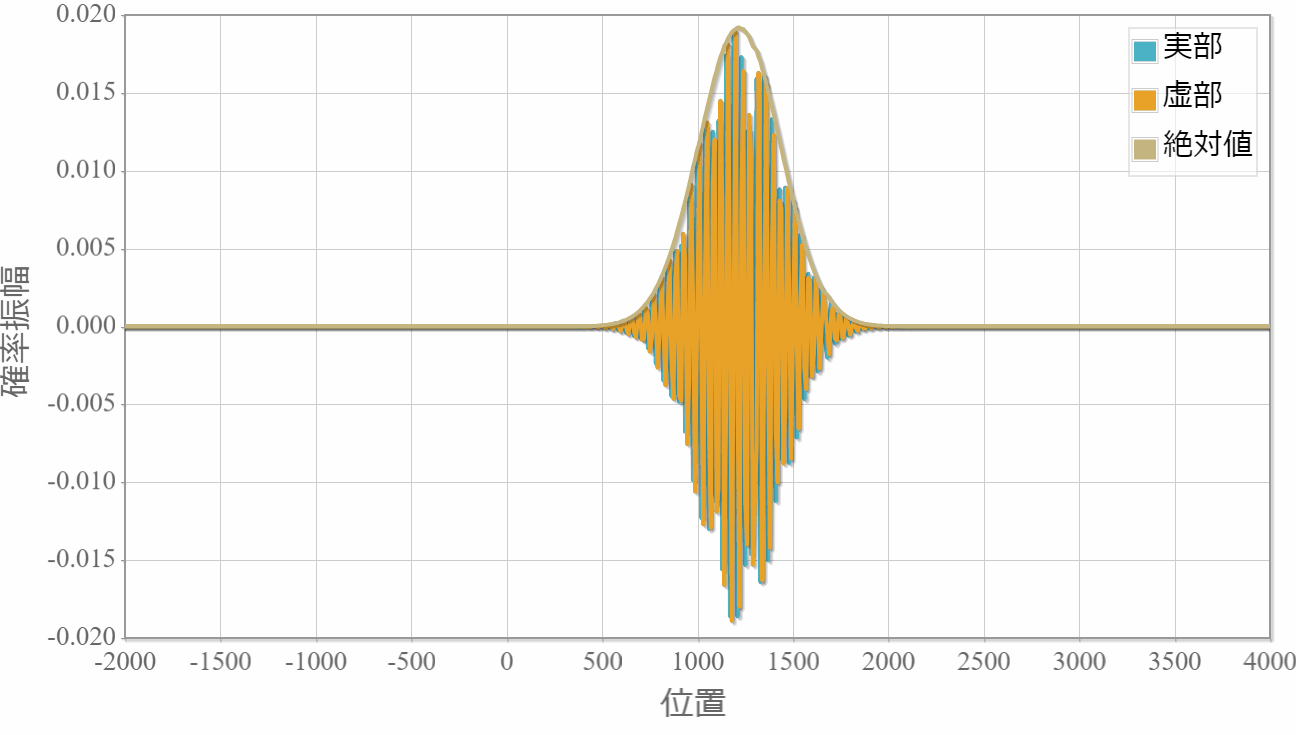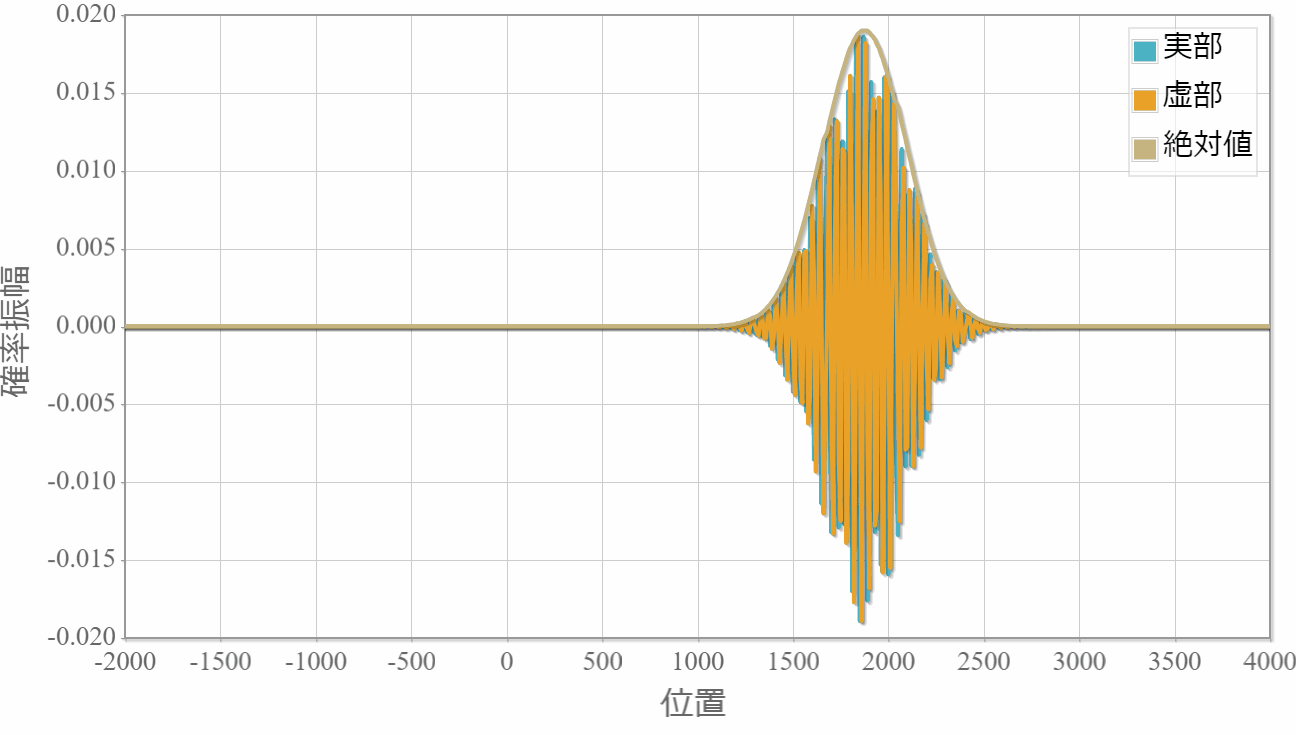
時間スケール：5E-16[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：200
フーリエ級数展開係数の項数：2048
ルンゲ・クッタの時間刻み幅：1.0E-19[s]

パラメータの設定方法

フーリエ級数展開係数の項数

スペクトル法は波動関数を空間分布をフーリエ級数展開して、その展開係数の時間発展を数値的に計算します。そのため、空間分布をフーリエ級数展開したときの波数が、波束を構成する波数を含んでいる必要があります。つまり、中心エネルギーが大きいほど、また、Lを大きくするほど、フーリエ級数展開係数の項数を大きくする必要があります。

,

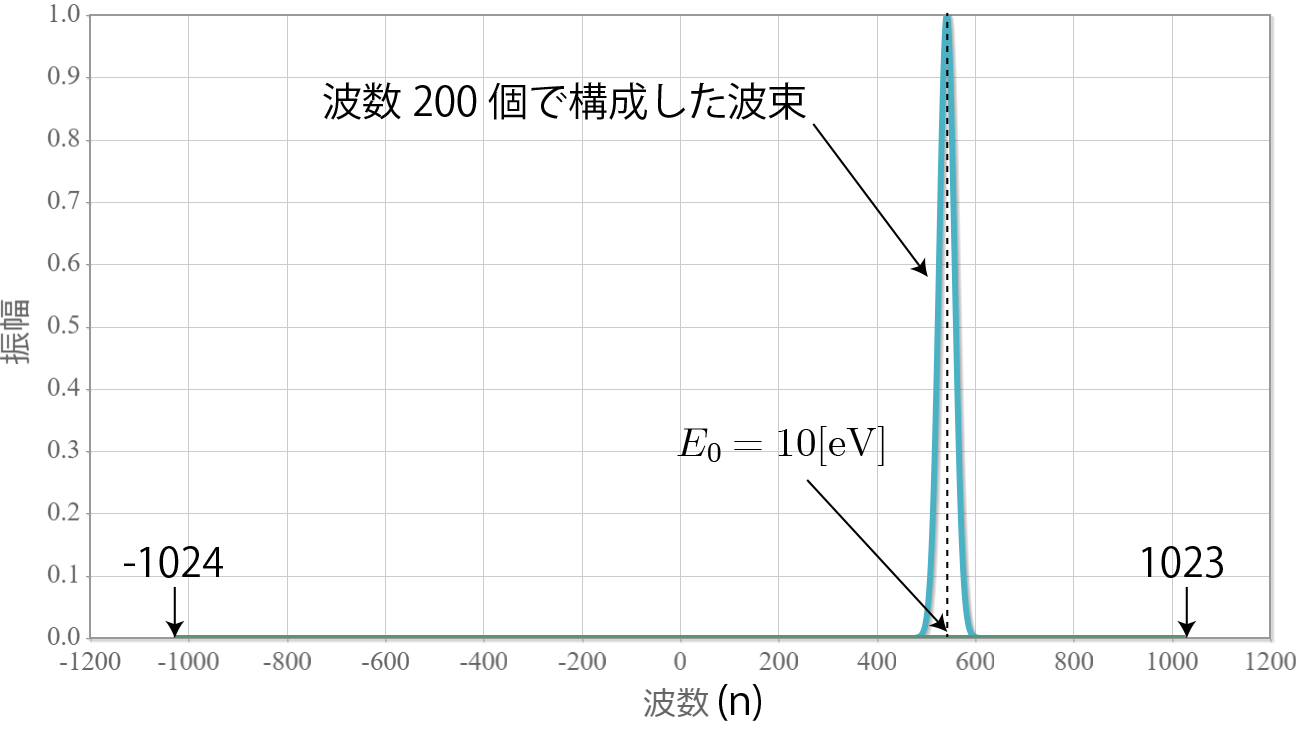
次の図は、中心エネルギーE0=10eVの波束を構成する波数のフーリエ級数展開です。E0=10eVの波束を構成する波数を完全に含むには1024個では全く足りず、2048個が必要となります。 なお、中心エネルギーを更に上げるには更に多くの項数が必要となります。

ルンゲ・クッタの時間刻み幅

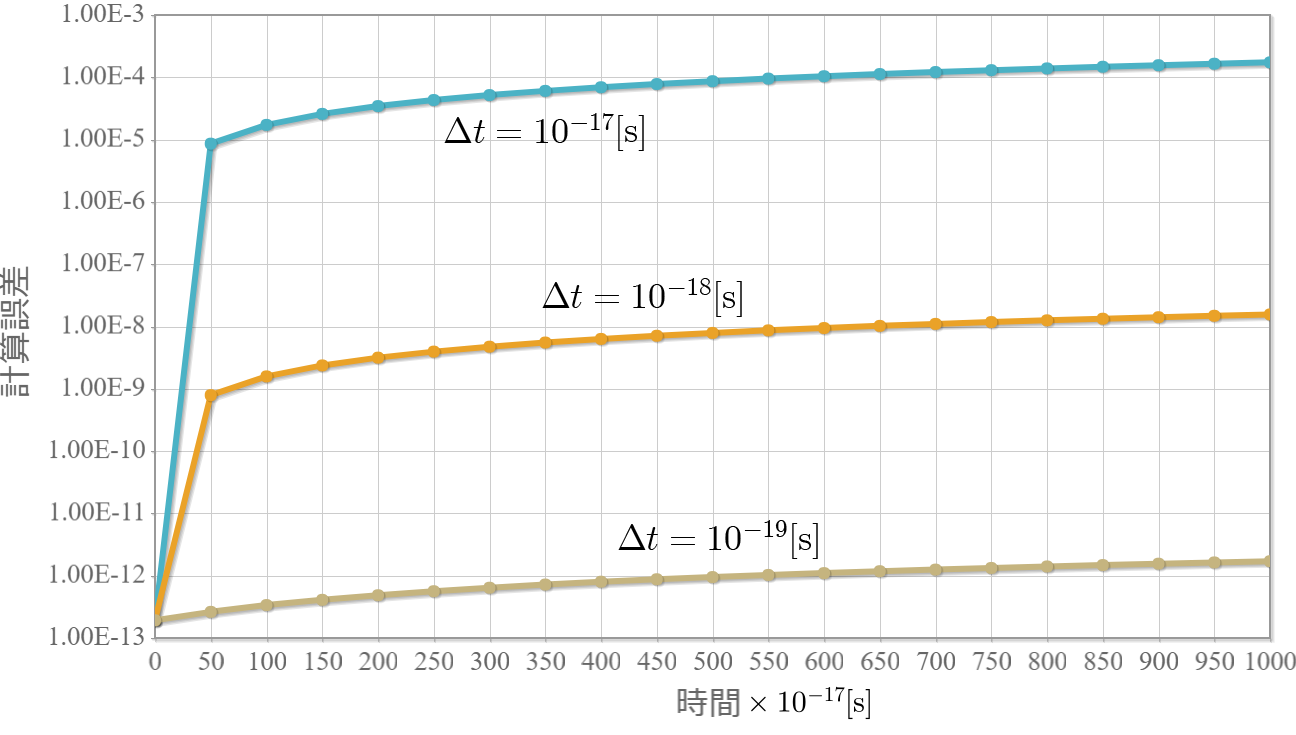
次の図は時間発展を計算するルンゲクッタ法の時間刻み幅を1E-17[s], 1E-18[s], 1E-19[s]とした際の計算誤差（実空間における１点あたりの誤差の平均）です。時刻０の誤差が1E-13なので、これが基準になります。まず、時刻の刻み幅を1/10にすると、誤差が1E-4倍となっていることから、ルンゲクッタ法の４次精度が実現できていることがわかります。また、時間刻みが1E-19[s]の場合に、初期誤差からなめらかな増加となっていることから、この時間刻みで十分であることがわかります。ちなみに、更に誤差をさせるには波束を構成する波数の数を増やすことで実現できます。

次回は箱型ポテンシャル障壁への衝突で解析解と比較します。

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics_OpenMP.zip
※VisualC++、GCC（MinGW）で動作確認しています。