【量子力学再入門17】
空間一様時間依存ポテンシャル中の波束の運動

対応する具体的な物理系は思い浮かびませんが、空間的には一様で時間に依存するポテンシャル中を運動する波束を調べてみます。
※数値計算法のスペクトル法についてはこちらを参照ください

\begin{align} V(t) = V_0 \sin(\omega t) \end{align}

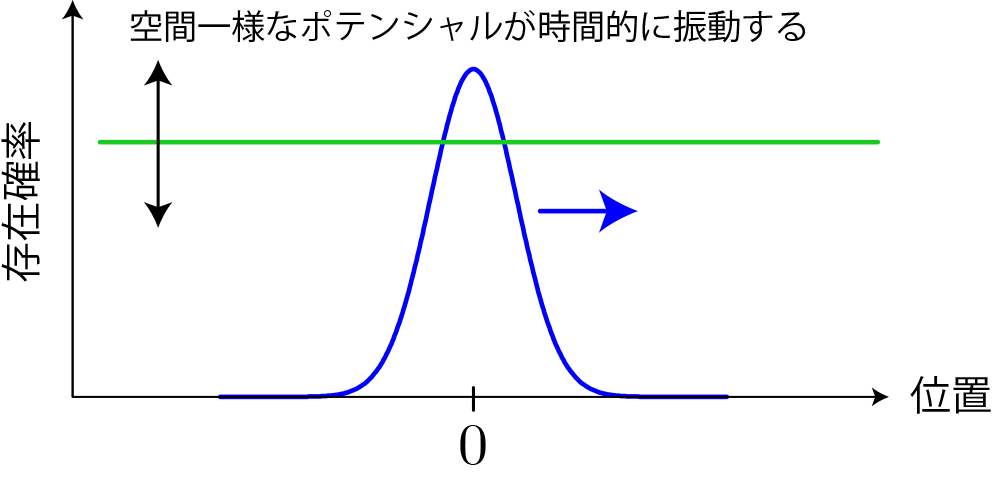
シミュレーション結果

波束の中心エネルギー2eV、周期$T=10^{-15}[{\rm s}]$、振幅$V_0=10[{\rm eV}]$のポテンシャル（波束がもつエネルギーよりもポテンシャルの大きさの方が大きい）。

時間スケール：4E-15[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：4096
ルンゲ・クッタの時間刻み幅：1.0E-17[s]

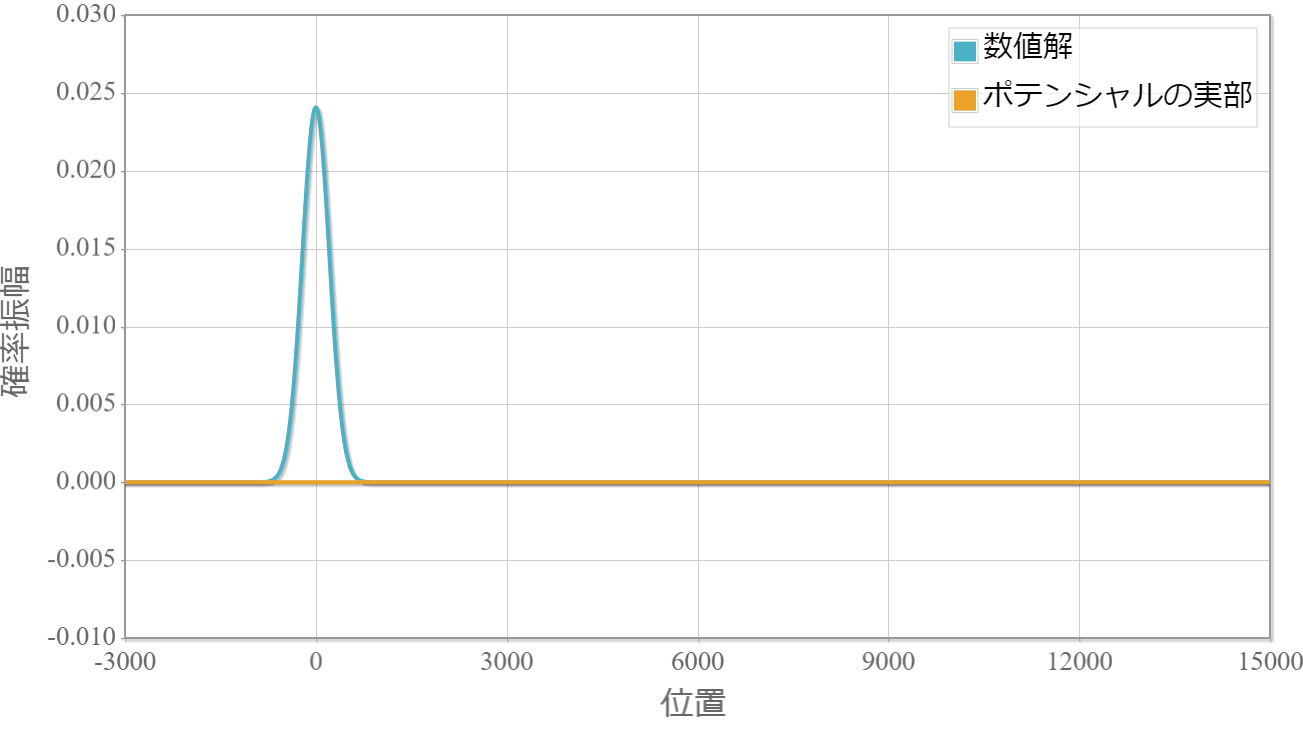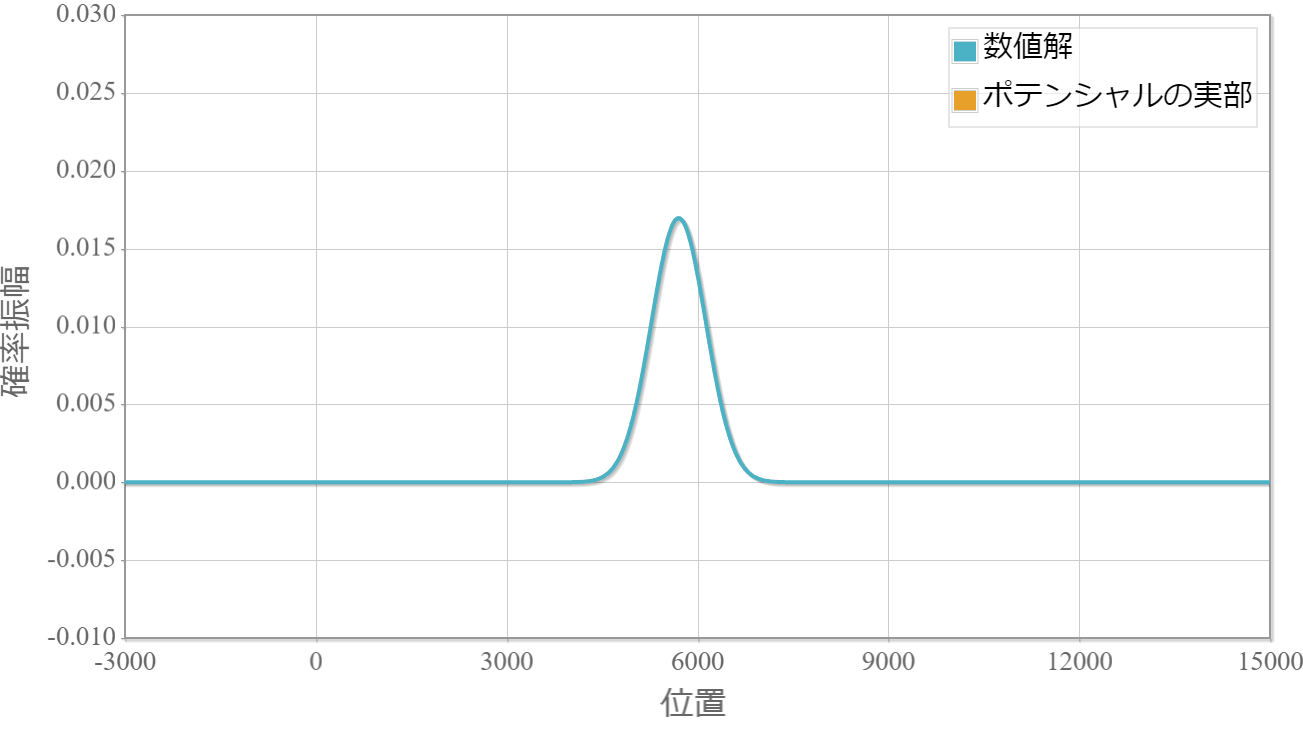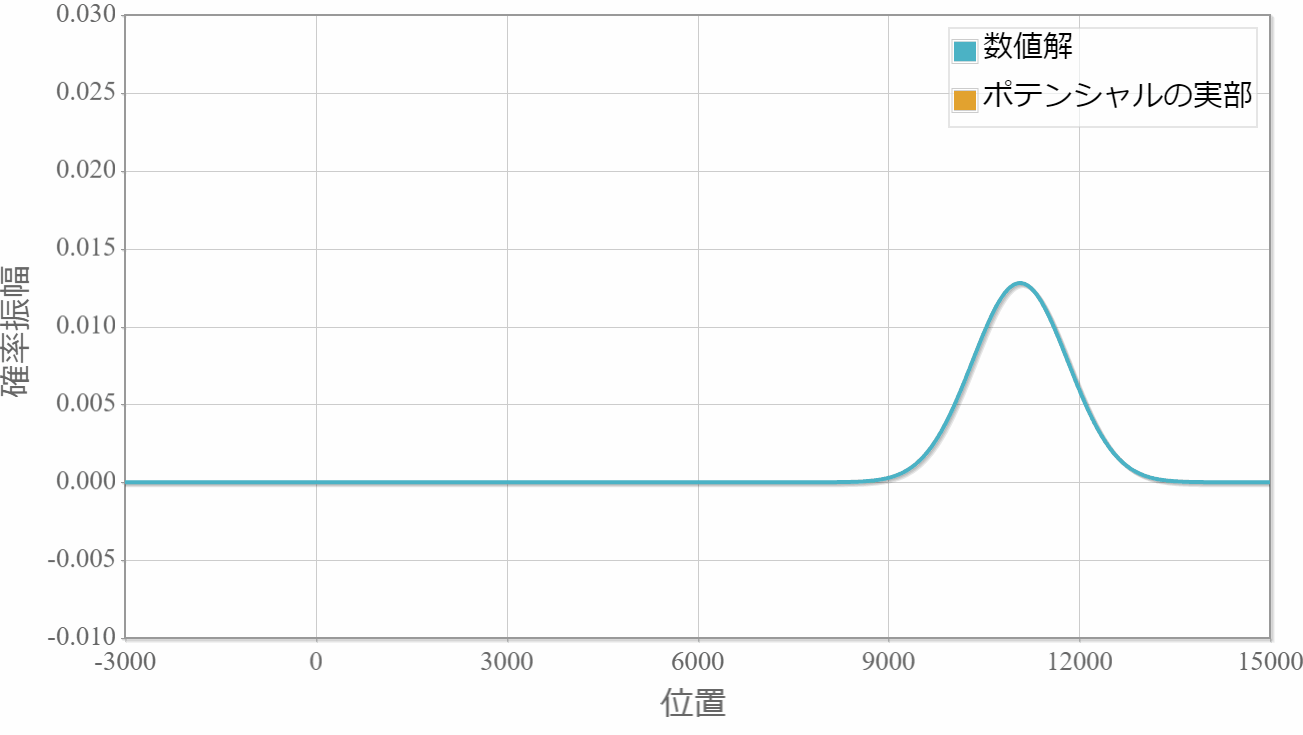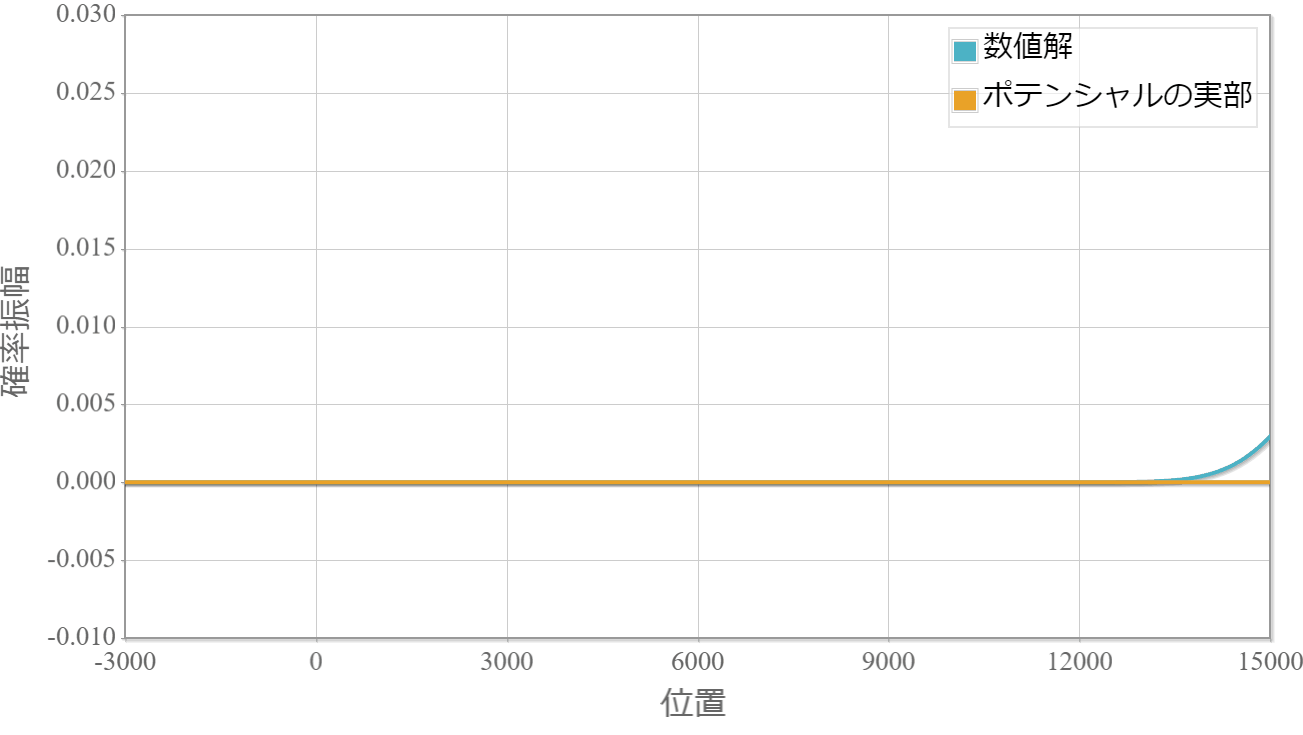
てっきり波束は壊れるかと思っていましたが、空間一様の場合には波束はどんなに大きなポテンシャルでも影響を受けずにそのまま進んでいきます。 これはシュレディンガー方程式

\begin{align} i\hbar \, \frac{\partial \psi(x,t)}{\partial t} = -\frac{\hbar^2}{2m} \, \frac{\partial^2 \psi(x,t)}{\partial x^2} +V(t) \psi(x,t) \end{align}

から直接導出できます。波動関数の一般解は次のとおりです。

\begin{align} \psi(x,t)=\sum\limits_{n}a_n(0) e^{ik_nx-i\omega_n t}e^{-\frac{i}{\hbar}\int_{0}^t V(t')dt'} \end{align}

ポテンシャルの時間依存性は波動関数の位相を変化させる効果しか与えないことがわかりました。

今後の計算予定（メモ）

・２重量子井戸の場合

プログラムソース（C++）

・http://www.natural-science.or.jp/files/physics/QuantumPhysics17.cpp
※VisualC++、GCC（MinGW）で動作確認しています。