【量子力学再入門22】
幅が変化する量子井戸内の波束の運動（スペクトル法）
文責：遠藤 理平 （2018年6月21日）
カテゴリ：計算物理学(165)
今回は幅が変化する量子井戸内の波束の運動をスペクトル法を用いてシミュレーションします。
※数値計算法のスペクトル法についてはこちらを参照ください
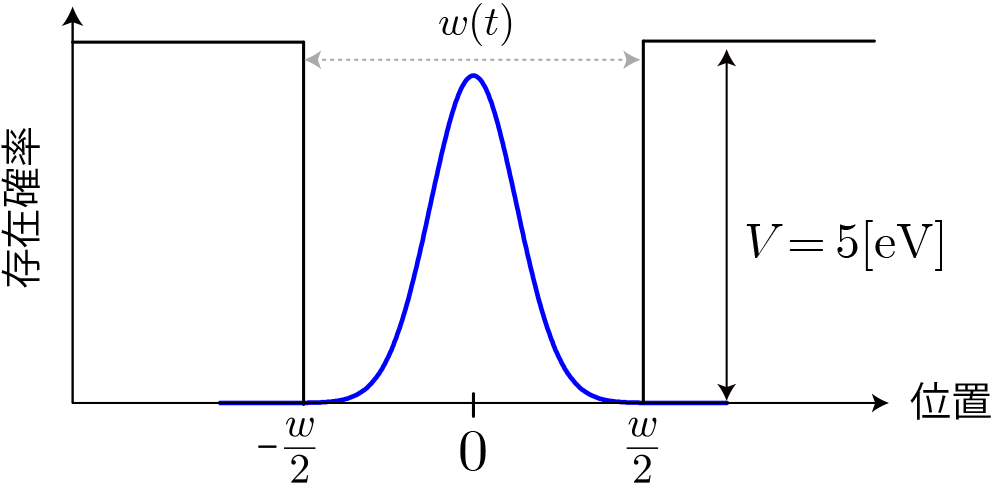
シミュレーション結果
高さ$V_0=5.0\times 10^{-8} [{ \rm eV}]$の量子井戸内に、中心エネルギー$0 [{ \rm eV}]$の波束を配置した際の運動です。
$w_0= 1500\times 10^{-11}[{ \rm m}]$
$A= 500\times 10^{-11}[{ \rm m}]$
$\omega= 2\pi \times 10^{7}[{ \rm rad/s}]$
時間スケール：4E-15[s]（１コマ）
空間スケール：1E-11[m]
波束を生成する平面波の項数：500
フーリエ級数展開係数の項数：4096
ルンゲ・クッタの時間刻み幅：1.0E-17[s]
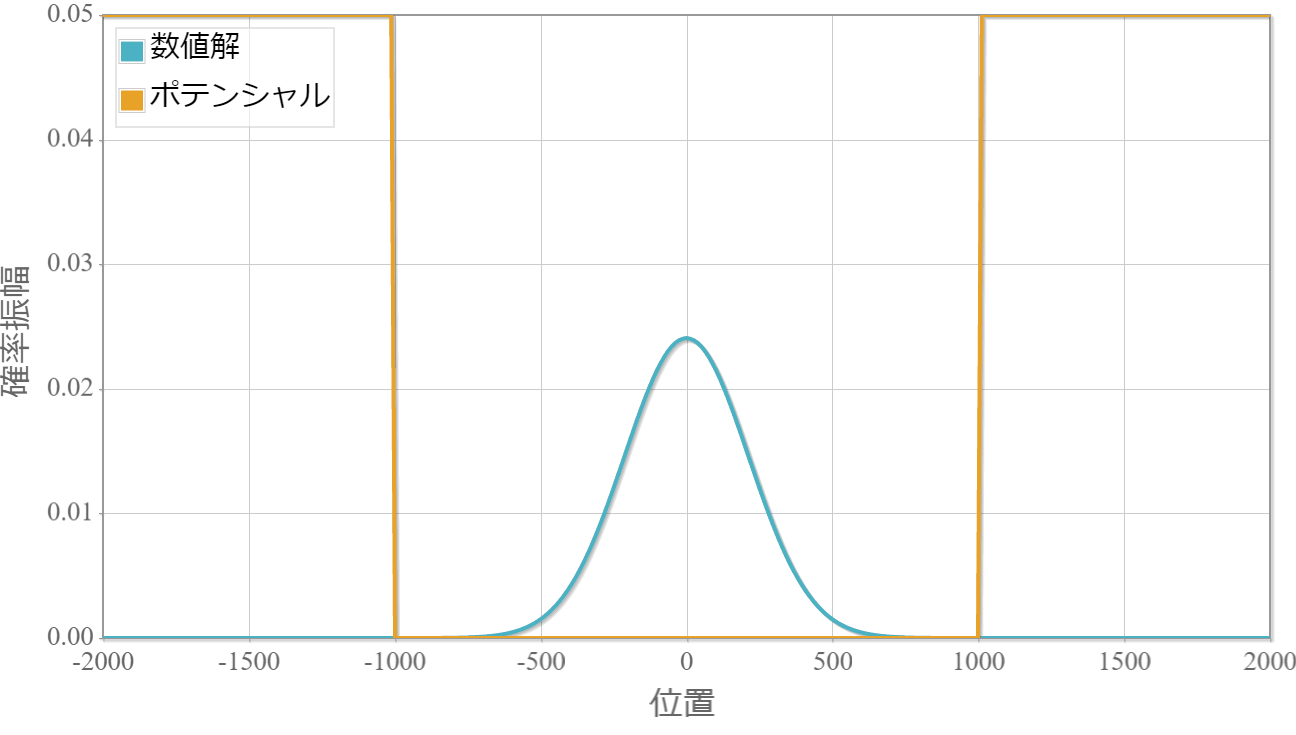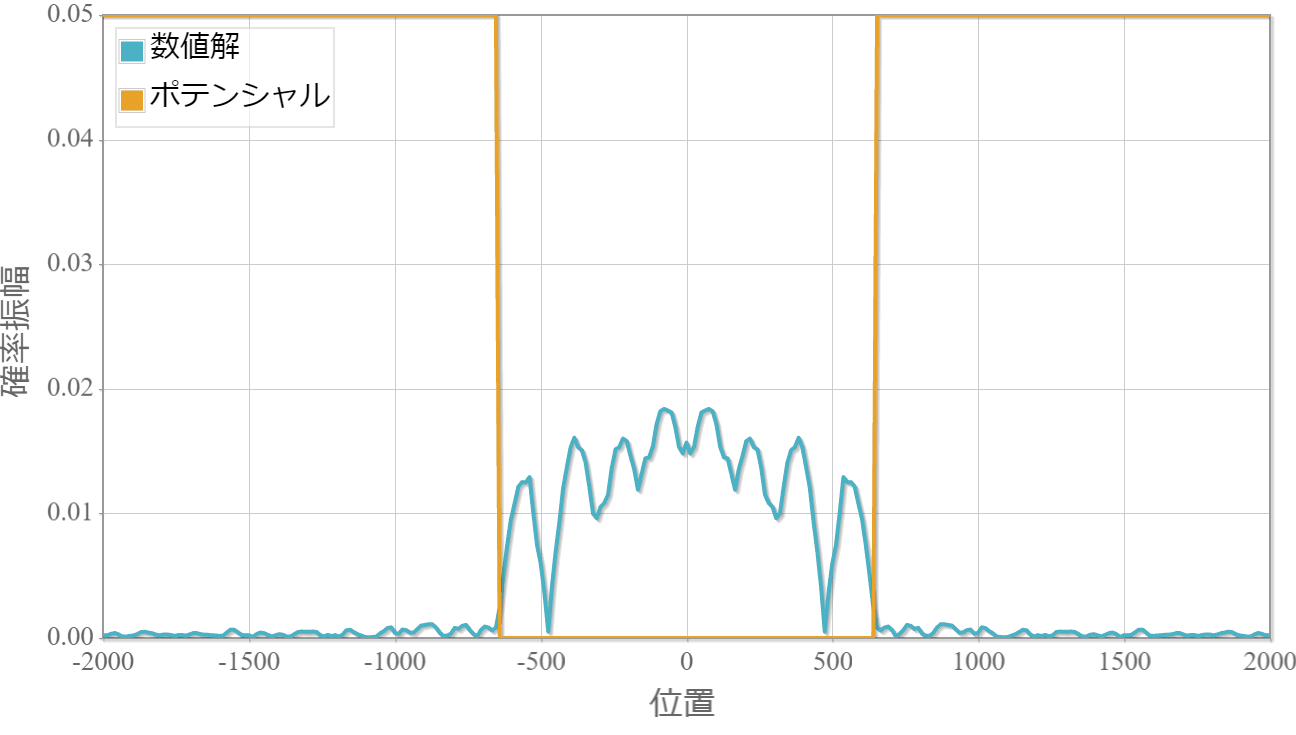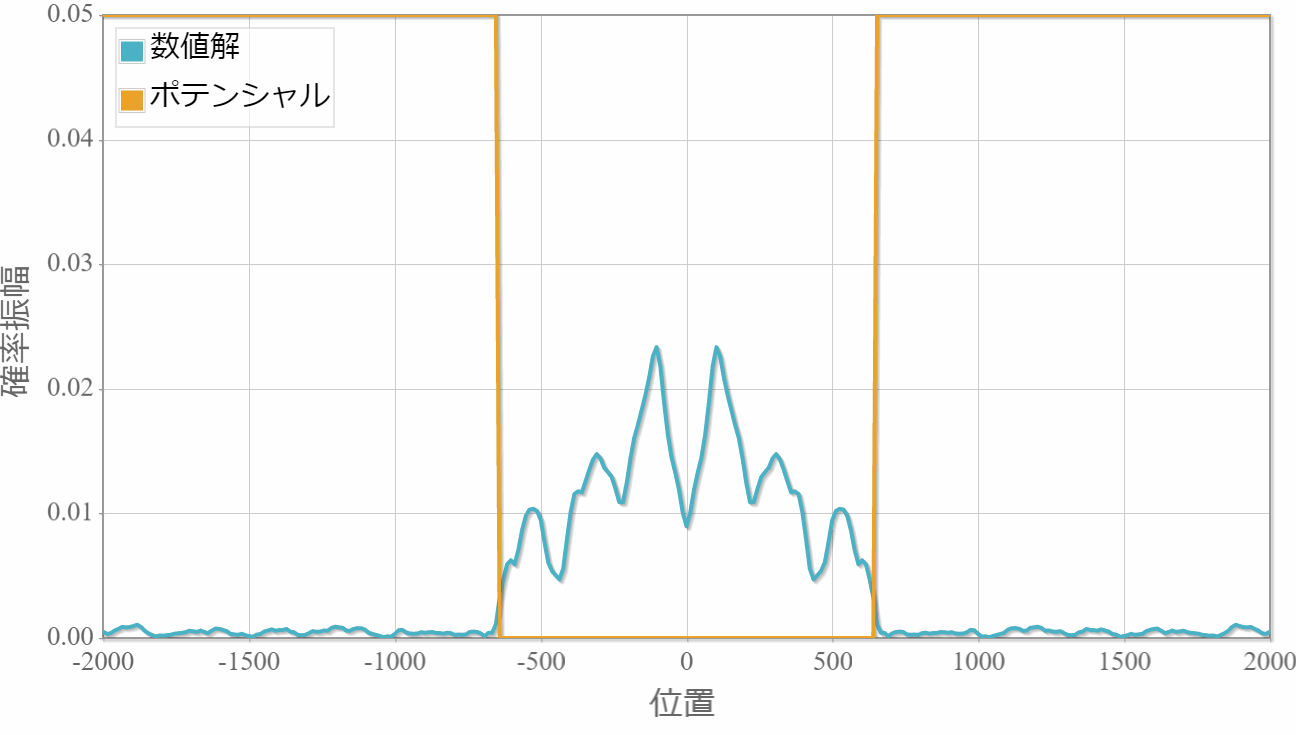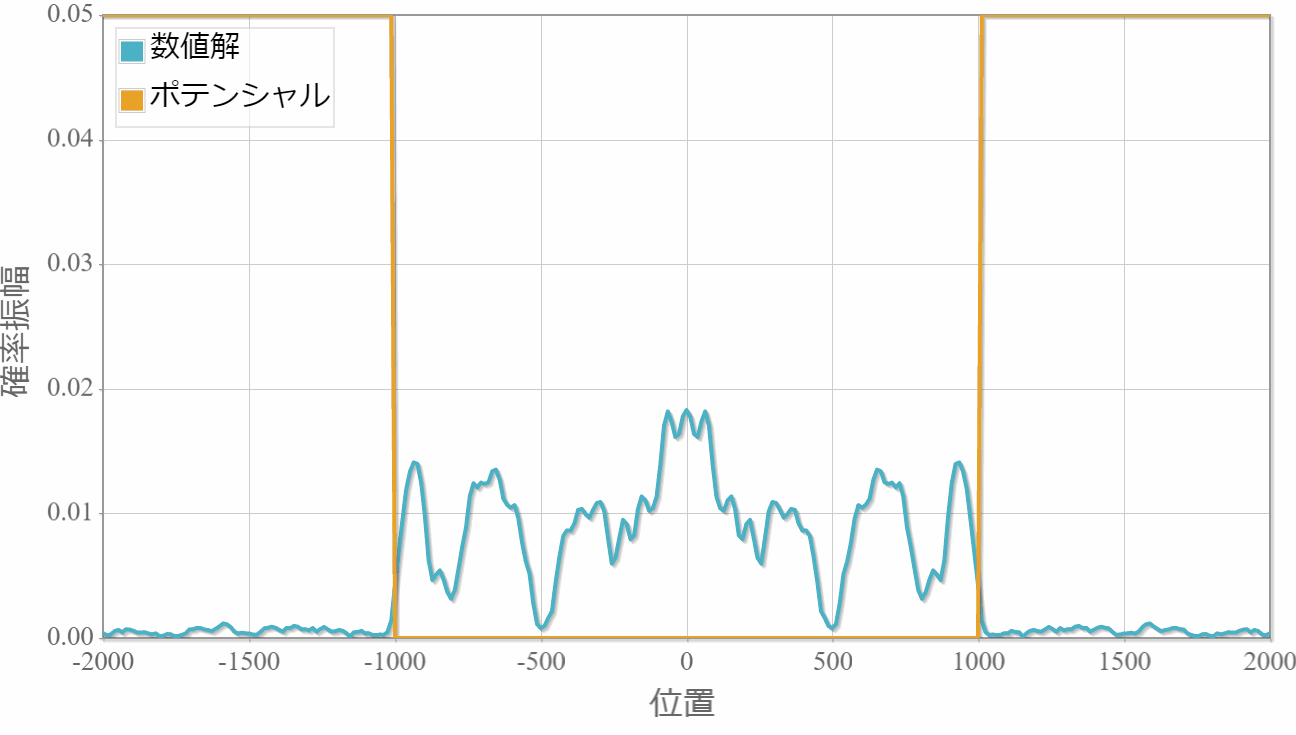
幅に合わせて波束が伸び縮みする様子がわかる。
今後の計算予定（メモ）
・量子井戸の幅を変化させることによる励起状態を調べる
プログラムソース（C++）
・http://www.natural-science.or.jp/files/physics/QuantumPhysics22.cpp
※VisualC++、GCC（MinGW）で動作確認しています。
