計算物理学　第１章序章
１－１．Duffing振動子のカオス的運動のシミュレーション

本稿は、凝縮系物理を中心として広範囲にわたる計算手法に関して、そのアルゴリズムの導出から実装までを丁寧にまとめられていることで知られている計算物理学 J.M.ティッセン (著), (訳) 松田 和典, 道廣 嘉隆, 谷村 吉隆, 高須 昌子, 吉江 友照を元に、 本書で取り扱われているテーマについて、具体的にC++言語にてプログラミングし、計算結果を gnuplot や OpenGL を用いて図や動画にすることを目的とします。

本書では計算物理学において、決定論的な運動の例としてニュートン運動方程式で現れるカオス現象を取り上げています。Duffing（ダフィング）振動子は、パラメータによってカオス運動をすることが知られています。

ニュートンの運動方程式

ニュートン運動方程式とは、質量を持つ物体に力が加えられた際に、力と生じる物体の加速度との関係を表した方程式です。（参考：コンピュータシミュレーション講座のテキスト
【2-1-1】加速度・力・質量の関係：ニュートンの運動方程式）

(1)

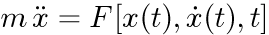
Duffing振動子

Duffing振動子とは、鉄製の振り子と磁石がセットされた台を振動させることで実験することができます。 鉄球に加わる力は次のように与えられます。

(2)

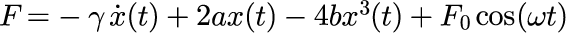
第１項は速度に比例した摩擦力を、 第２項と第３項は重力・張力・磁力でつくられる２重の井戸を表し、 最後の項は、強制振動力を表しています。 式(2)を式(1)に代入することで、ニュートン運動方程式が完成します。

(3)

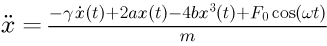
式(3)は２階の常微分方程式なので、運動を決定するためには２つの初期条件（位置と加速度）が必要になります。 さらに、コンピュータで解くためには、式(3)の６つのパラメータを与える必要があります。 計８つのパラメータの内４つを次の値で固定し、残りの４つを変化させて違いを観察します。

(4)

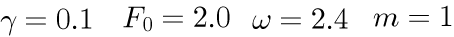
計算結果

２つの事例について、計算結果を紹介します。

１．カオス運動を行う２つの振動子の初期値による違い

赤線と緑線は、初期位置がごくわずか異なる場合の時間発展を表しています。
横軸：時間 t[s]
縦軸：位置 x[m]

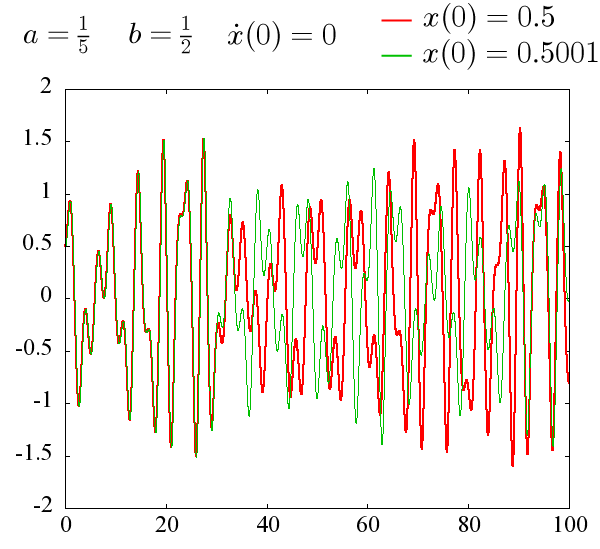
はじめの違いはごくわずかでも、少しずつずれが大きくなり、お互いの運動は互いに無秩序で予測不可能的な運動を繰り返していることがわかります。 一般的にカオス運動とはこのことを指します。

２．初期値によって、アトラクタが異なる例

赤と緑の線は、上記と同様初期位置がごくわずか異なる場合の時間発展を表しています。
横軸：時間 t[s]
縦軸：位置 x[m]

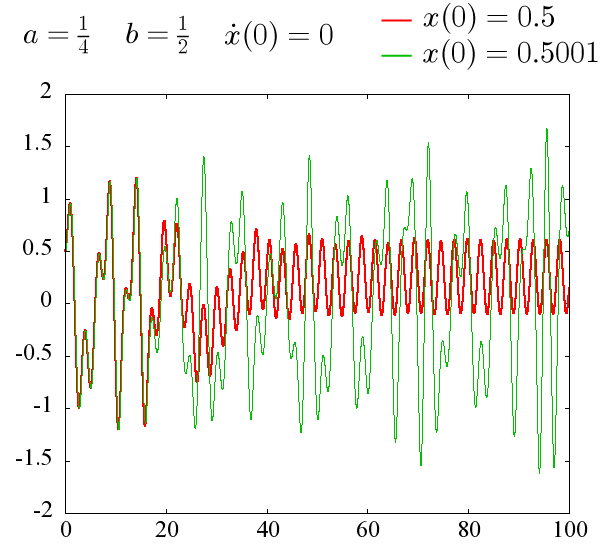
はじめの違いはごくわずかにも関わらず、赤線は途中から周期運動になり、緑線はいつまでもカオス的運動を繰り返していることが確認できます。

C++プログラム

上記のような常微分方程式を計算する際によく利用されるルンゲクッタ法（４次）を適用します。 比較したい２つの軌道を計算し、ファイル出力します。 さらに、計算結果を同時に gnuplot を使用してグラフ描画を行います。

 
//////////////////////////////////////////////////////////////////////////
// Duffing振子
// Duffing振子_ルンゲクッタ_２つの軌道の比較.cpp
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <direct.h>
#include <time.h>
using namespace std;
double PI = acos(-1.0);

//////////////////////////////////////////////////////////////////////////
// 変数の定義
//////////////////////////////////////////////////////////////////////////
ofstream file1( "Duffing.data" );
//--------------------------------------------------------
// 仮想物理実験室変数の定義
//--------------------------------------------------------
double t = 0.0;       //時刻
double t_end = 100.0; //計算を終了する時刻
double dt= 0.001;     //時間刻み
int skipDat = 10;     //データ書出し回数の間引き回数

double F0    = 2.0;
double omega = 2.4;
double gamma = 0.1;
 
struct PENDULUM {//振り子の構造体
  double m;
  double a, b;
  double x;
  double vx;
};
PENDULUM pendulum1, pendulum2; //振り子１と振り子２
void SetUp(void){
  pendulum1.x = 0.5;
  pendulum1.vx= 0.0;
  pendulum1.m= 1.0;
  pendulum1.a= 1.0/5.0;
  pendulum1.b= 1.0/2.0;
  pendulum2.x = 0.5001;
  pendulum2.vx= 0.0;
  pendulum2.m= 1.0;
  pendulum2.a= 1.0/5.0;
  pendulum2.b= 1.0/2.0;
}
//////////////////////////////////////////
// ルンゲクッタ用
void RungeKutta4(PENDULUM *pendulum);

//////////////////////////////////////////////////////////////////////////////////
// メイン関数
//////////////////////////////////////////////////////////////////////////////////
int main(){
  SetUp();
  for(int tn=0; tn <= int(t_end/dt) ;tn++){
    t =dt*tn;
    RungeKutta4( &pendulum1);
    RungeKutta4( &pendulum2);
    if(tn%skipDat == 0){
      file1 << t << " " <<  pendulum1.x <<  " " <<  pendulum1.m * pendulum1.vx << " " <<  pendulum2.x <<  " " <<  pendulum2.m * pendulum2.vx << endl;
    }
  }
  //////////////////////////////
  //gnuplotによる描画
  FILE *fp = _popen( "C:/gnuplot/bin/pgnuplot.exe" , "w"); //gnuplotのパイプ用の実行ファイル
  if (fp == NULL) return -1; 
  fputs("set terminal gif optimize size 600, 480\n", fp);
  fputs("set tics font \'Times,18\'\n", fp);
  fputs("set output \"Duffing.gif\"\n", fp);
  fputs("set rmargin 4\n", fp);
  fputs("set nokey\n", fp);
  //fputs("set yr[0:70]\n", fp);
  //t-x
  fputs("plot \"Duffing.data\" u 1:2 w l lw 2 , \"Duffing.data\" u 1:4 w l lw 1 \n", fp);
  fflush(fp);
  _pclose(fp);
  //cin.get();
  ///////////////////////////////
  return 0;
}

/////////////////////////////////////////////
// ルンゲクッタ
double f1(double t, double x, double vx, double m, double a, double b){
  return vx;
}
double f2(double t, double x, double vx, double m, double a, double b){
  return -gamma/m*vx + 2.0*a/m*x - 4.0*b/m*pow(x,3) + F0/m*cos(omega*t); 
}
void RungeKutta4(PENDULUM *pendulum){
  double k1[2],k2[2],k3[2],k4[2];
  double x  = pendulum->x;
  double vx = pendulum->vx;
  double m  = pendulum->m;
  double a  = pendulum->a;
  double b  = pendulum->b;
  k1[0]=dt*f1(t, x, vx, m, a, b);
  k1[1]=dt*f2(t, x, vx, m, a, b);
  k2[0]=dt*f1(t+dt/2.0,x+k1[0]/2.0,vx+k1[1]/2.0, m, a, b);
  k2[1]=dt*f2(t+dt/2.0,x+k1[0]/2.0,vx+k1[1]/2.0, m, a, b);
  k3[0]=dt*f1(t+dt/2.0,x+k2[0]/2.0,vx+k2[1]/2.0, m, a, b);
  k3[1]=dt*f2(t+dt/2.0,x+k2[0]/2.0,vx+k2[1]/2.0, m, a, b);
  k4[0]=dt*f1(t+dt,x+k3[0],vx+k3[1], m, a, b);
  k4[1]=dt*f2(t+dt,x+k3[0],vx+k3[1], m, a, b);
  pendulum->x   = pendulum->x  + (k1[0]+2.0*k2[0]+2.0*k3[0]+k4[0])/6.0;
  pendulum->vx  = pendulum->vx + (k1[1]+2.0*k2[1]+2.0*k3[1]+k4[1])/6.0;
}

課題メモ

１．gnuplot を使用してDuffing振子の位相空間上でのカオス的運動のアニメーションを作成する
２．Duffing振動子に対するストレンジ・アトラクタのフラクタル次元を計算する
３．Duffing振動子の方程式を実現する実験系に即したシミュレーションを行う → OpenGL を用いてアニメーションの作成

ミスの指摘、質問、コメントなどがございましたら、HTMLフォーム、もしくはinfo:natural-science.or.jpから、お待ちしております。

目次

第１章　序章

• １－１．Duffing振子のカオス的運動のシミュレーション
• １－２．Duffing振子の位相空間上でのカオス的運動のアニメーション
• １－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元
• ２－１．DLAによる樹木状クラスタのシミュレーション
• ２－２．DLAによる樹木状クラスタのフラクタル次元

第２章　対称ポテンシャルによる量子散乱

ゴール：水素原子のクリプトン原子による散乱に対する散乱断面積の計算

• ・ヌメロフ法による常微分方程式の解法
• ・球ベッセル関数
• ・ルジャンドル多項式
• ・位相シフト→断面積を計算するアルゴリズム

その他

• ・擬似乱数生成器：メルセンヌ・ツイスタの使い方
• ・ランダムウォークによる擬似乱数の比較：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)