計算物理学　第１章序章
１－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元

本稿は、凝縮系物理を中心として広範囲にわたる計算手法に関して、そのアルゴリズムの導出から実装までを丁寧にまとめられていることで知られている計算物理学 J.M.ティッセン (著), (訳) 松田 和典, 道廣 嘉隆, 谷村 吉隆, 高須 昌子, 吉江 友照を元に、 本書で取り扱われているテーマについて、具体的にC++言語にてプログラミングし、計算結果を gnuplot や OpenGL を用いて図や動画にすることを目的とします。

カオス的運動の特徴は、ニュートン運動方程式にしたがって運動する決定論的であるにも関わらず、その軌道が予測しえない複雑さを持つ点です。 コンピュータ・シミュレーションでは再現可能である一方、実験的には初期値敏感性のために再現が困難となります。 このようなカオス的運動の特徴を位相空間における軌道のフラクタル性に注目して、その「フラクタル次元」を見積もることで、定量的に評価する手法があります。

前節では、Duffing振動子の位相空間上でのカオス的運動のアニメーションを行いました。 振動子は２次元の位相空間上を時間とともに連続に移動しますが、時間軸を含めると３次元の位相空間上の軌道としていると考えられます。 複雑な３次元の位相空間上の運動の特徴を調べるために、 この系の特徴的な時間を表すパラメータである強制振動の周期 T = 2π/ω[s]ごとに位相空間上の座標を取り出す作業を行います。 こうしてできる点の集合はポアンカレ断面と呼ばれます。 そしてその点の分布から振動子の運動の特徴を調べることができます。

Duffing方程式のパラメータ

(1)

(2)

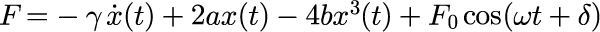
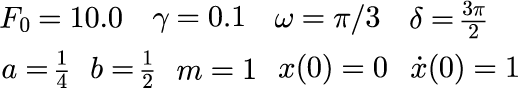
Duffing振動子のポアンカレ断面

周期 T = 2π/ω[s] ごとに、振動子の位相空間上での位置をプロットした結果です。 プロット数は 100000 です。

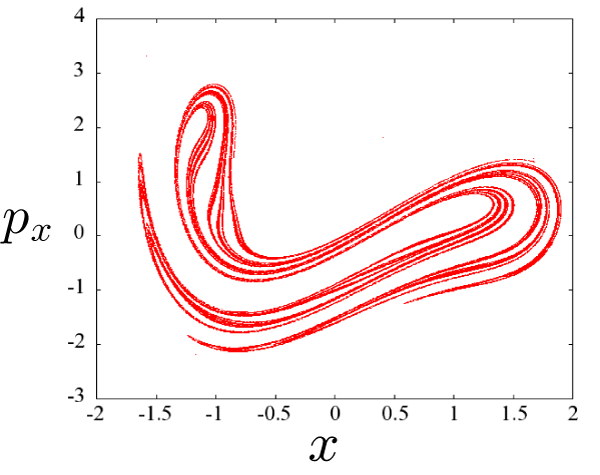
このような集合は、カオス理論でしか説明のつかないアトラクタで、ストレンジ・アトラクタと呼ばれています。

ストレンジ・アトラクタのフラクタル次元の計算

フラクタルとは、集合の一部が集合の全部と相似であるようなものをいいます。 上記のストレンジ・アトラクタはフラクタルではないのですが、 一般的に一様でない集合に対して、一様の度合いをあらわす指標として、フラクタル次元を定義します。

フラクタル次元の定義は数多くの種類がありますが、 今回はもっとも単純な容量次元を取り扱います。 容量次元を計算する手順は次のとおりです。
１．一辺が L の n次元の立方体で集合全体を覆うことを考えます。
（今回は２次元集合なので n=2 つまり正方形）
２．集合全体を覆うのに必要な立方体の個数を N とします。
３．L に対する N をプロットします。
４．次の式で与えられる Df が容量次元です。

(3)

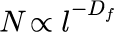
計算結果：NとLの関係

縦軸：覆うのに必要な立方体の個数
横軸：立方体の一辺の長さ
※注意：両対数プロットです

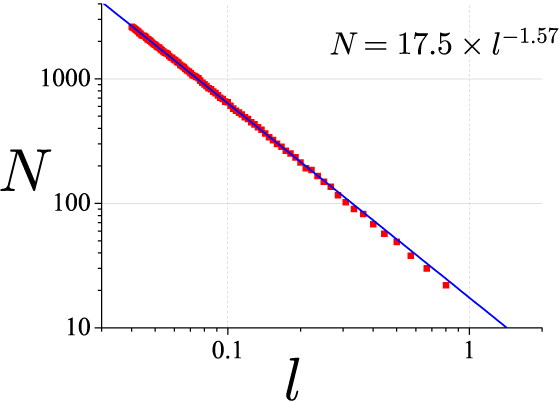
立方体の一辺の長さ を小さくするにしたがって、傾きが一定になっているのがわかります。 （両対数プロットなので、傾きは指数部分になります）
Duffing振動子のポアンカレ断面の容量次元は、D_f= 1.57 程度となることが知られています。

２次元平面状の点の集合なので、容量次元は２未満となります。
・振動子の運動が周期的であれば、軌道は２次元平面上の１点のみ → ０次元
・振動子の運動が規則的に変化するのであれば、軌道は２次元平面上で直線的 → １次元
・振動子の運動が不規則に変化するのであれば、軌道は２次元平面上を蛇行 → １次元以上２次元未満
・（ありえないが）振動子の軌道が、２次元平面上を埋め尽す → ２次元

今回の結果は、位相空間上を不規則に変化していることがわかります。 容量次元はその度合いを表しています。

参考（フラクタル次元）

・multifractal（マルチフラクタル）概説
・カントール集合のマルチフラクタル(multi-fractal)解析

C++プログラムソース

Duffing振動子におけるポアンカレ断面のgnuplot による描画と、容量次元を計算するプログラムです。

 
//////////////////////////////////////////////////////////////////////////
// Duffing振子
// ストレンジアトラクタ
//////////////////////////////////////////////////////////////////////////
#include <math.h>
#include <fstream>
#include <sstream>
#include <iostream>
#include <direct.h>
#include <time.h>
using namespace std;
double PI = acos(-1.0);

//////////////////////////////////////////////////////////////////////////
// 変数の定義
//////////////////////////////////////////////////////////////////////////
ofstream file1( "Duffing.data" );
ofstream file2( "Duffing_dimension.data" );
//--------------------------------------------------------
// 仮想物理実験室変数の定義
//--------------------------------------------------------

double F0    = 10.0;
double omega = 2.0*PI/6.0;
double gamma = 0.1;
double delta = PI*1.5;

const int N=100000;
double T = 2.0*PI/omega; //周期
double t = 0.0;          //時刻
double t_end = N * T;  //計算を終了する時刻
double dt= 0.001 * T ;   //時間刻み
int skipDat = 1000;      //データ書出し回数の間引き回数

struct PENDULUM {
  double m;
    double a, b;
  double x;
  double vx;
};
PENDULUM pendulum1;
void SetUp(void){
    pendulum1.x = 0.0;
    pendulum1.vx= 1.0;
    pendulum1.m= 1.0;
    pendulum1.a= 1.0/4.0;
    pendulum1.b= 1.0/2.0;
}

struct POINTS {
    double x;
    double px;
};
POINTS points[N];
double gx  = 0.0;//位相空間における分布の重心座標
double gpx = 0.0;

//////////////////////////////////////////
// ルンゲクッタ用
void RungeKutta4(PENDULUM *pendulum);

//////////////////////////////////////////////////////////////////////////////////
// メイン関数
//////////////////////////////////////////////////////////////////////////////////
int main(){
  SetUp();
  for(int tn=0; tn <= int(t_end/dt) ;tn++){
    t =dt*tn;
    RungeKutta4( &pendulum1);
    if(tn%skipDat == 0){
            points[int(t/T)].x  = pendulum1.x;
            points[int(t/T)].px = pendulum1.m * pendulum1.vx;
            gx  += pendulum1.x /N;
            gpx +=  pendulum1.m * pendulum1.vx /N;
    }
  }
    //位相空間上の分布の重心を原点にずらす
    for(int i=0; i<N; i++){
        points[i].x  -= gx;
        points[i].px -= gpx;
        file1 << i << " " <<  points[i].x <<  " " <<  points[i].px << endl;
    }

    //////////////////////////////
    //gnuplotによる描画
    FILE *fp = _popen( "C:/gnuplot/bin/pgnuplot.exe" , "w"); //gnuplotのパイプ用の実行ファイルへのパス
    if (fp == NULL) return -1; 
    fputs("set terminal gif optimize size 600, 480\n", fp);
    fputs("set tics font \'Times,18\'\n", fp);
    fputs("set output \"Duffing.gif\"\n", fp);
    fputs("set rmargin 4\n", fp);
    fputs("set lmargin 6\n", fp);
    fputs("set nokey\n", fp);
    //fputs("set yr[0:70]\n", fp);
    //t-x
    fputs("plot \"Duffing.data\" u 1:2 w l lw 2 \n", fp);
    fflush(fp);

    fputs("set output \"Duffing_phase.gif\"\n", fp);
    fputs("set rmargin 4\n", fp);
    fputs("set lmargin 6\n", fp);
    fputs("set nokey\n", fp);
    //fputs("set yr[0:70]\n", fp);
    //t-x
    fputs("plot \"Duffing.data\" u 2:3 w d \n", fp);
    fflush(fp);
    _pclose(fp);
    ///////////////////////////////

    double w  = 4.0;
    int    nl = 10;
    int number_ =0;
    double dl_  =0.0;
    for(int k=3; k<= nl; k++){
        cout << k << endl;
        double dl = w/pow(2.0,k);
        int number = 0;
        for(int jx=0; jx<w/dl; jx++){
            for(int jpx=0; jpx<w/dl; jpx++){
                for(int i=0; i<N; i++){
                    if(-w/2.0+dl*jx <= points[i].x  &&  points[i].x  < -w/2.0+dl*(jx+1) && -w/2.0+dl*jpx <= points[i].px &&  points[i].px < -w/2.0+dl*(jpx+1)){
                        number++;
                        break;
                    }
                }
            }
        }
        if(number_!=0){    
            file2 << dl << " " <<  number <<  " " << - log(double(number)/double(number_))/log(dl/dl_) << endl;
        }
        number_ = number;
        dl_ = dl;
    }
    //cin.get();
    return 0;
}

/////////////////////////////////////////////
// ルンゲクッタ
double f1(double t, double x, double vx, double m, double a, double b){
  return vx;
}
double f2(double t, double x, double vx, double m, double a, double b){
  return -gamma/m*vx + 2.0*a/m*x - 4.0*b/m*pow(x,3) + F0/m*cos(omega*t+delta); 
}
void RungeKutta4(PENDULUM *pendulum){
  double k1[2],k2[2],k3[2],k4[2];
  double x  = pendulum->x;
  double vx = pendulum->vx;
  double m  = pendulum->m;
  double a  = pendulum->a;
  double b  = pendulum->b;
  k1[0]=dt*f1(t, x, vx, m, a, b);
  k1[1]=dt*f2(t, x, vx, m, a, b);
  k2[0]=dt*f1(t+dt/2.0,x+k1[0]/2.0,vx+k1[1]/2.0, m, a, b);
  k2[1]=dt*f2(t+dt/2.0,x+k1[0]/2.0,vx+k1[1]/2.0, m, a, b);
  k3[0]=dt*f1(t+dt/2.0,x+k2[0]/2.0,vx+k2[1]/2.0, m, a, b);
  k3[1]=dt*f2(t+dt/2.0,x+k2[0]/2.0,vx+k2[1]/2.0, m, a, b);
  k4[0]=dt*f1(t+dt,x+k3[0],vx+k3[1], m, a, b);
  k4[1]=dt*f2(t+dt,x+k3[0],vx+k3[1], m, a, b);
  pendulum->x   = pendulum->x  + (k1[0]+2.0*k2[0]+2.0*k3[0]+k4[0])/6.0;
  pendulum->vx  = pendulum->vx + (k1[1]+2.0*k2[1]+2.0*k3[1]+k4[1])/6.0;
}

課題メモ

１．さまざまなフラクタル次元の計算を行う。

ミスの指摘、質問、コメントなどがございましたら、HTMLフォーム、もしくはinfo:natural-science.or.jpから、お待ちしております。

目次

第１章　序章

• １－１．Duffing振子のカオス的運動のシミュレーション
• １－２．Duffing振子の位相空間上でのカオス的運動のアニメーション
• １－３．Duffing振子の位相空間上のストレンジ・アトラクタに対するフラクタル次元
• ２－１．DLAによる樹木状クラスタのシミュレーション
• ２－２．DLAによる樹木状クラスタのフラクタル次元

第２章　対称ポテンシャルによる量子散乱

ゴール：水素原子のクリプトン原子による散乱に対する散乱断面積の計算

• ・ヌメロフ法による常微分方程式の解法
• ・球ベッセル関数
• ・ルジャンドル多項式
• ・位相シフト→断面積を計算するアルゴリズム

その他

• ・擬似乱数生成器：メルセンヌ・ツイスタの使い方
• ・ランダムウォークによる擬似乱数の比較：C言語rand関数とメルセンヌ・ツイスタ(mt19937ar)